线性回归的一个问题可能是有可能出现欠拟合(如下图所示样本),因为它求的是具有最小均方误差的无偏估计。如果模型欠拟合将不能取得最好的预测效果。所以有些方法允许在估计中引入一些偏差,从而降低预测的均方误差。其中的一个方法是局部加权线性回归。在该算法中,我们给待预测点附近的每一个点赋予一定的权重,在这个子集上基于最小均方差来进行普通的回归。与KNN类似,这种算法每次预测均需要事先选取出对应的数据子集。该算法解出回归系数w的形式如下:
$\hat{\omega}=(X^TWX)^{-1}X^TWy$
其中$\omega$是一个矩阵,用来给每个数据点赋予权重。
局部线性加权使用核(类似支持向量机中的核)来对附近的点赋予更高的权重。核的类型可以自由选择,最常用的核就是高斯核,高斯核对应的权重如下:
$\omega(i,i)=exp\left(\frac{(x_i-x)^2}{-2k^2}\right)$
下图可以看到对应不同$k$值,高斯核对应的样本覆盖范围。
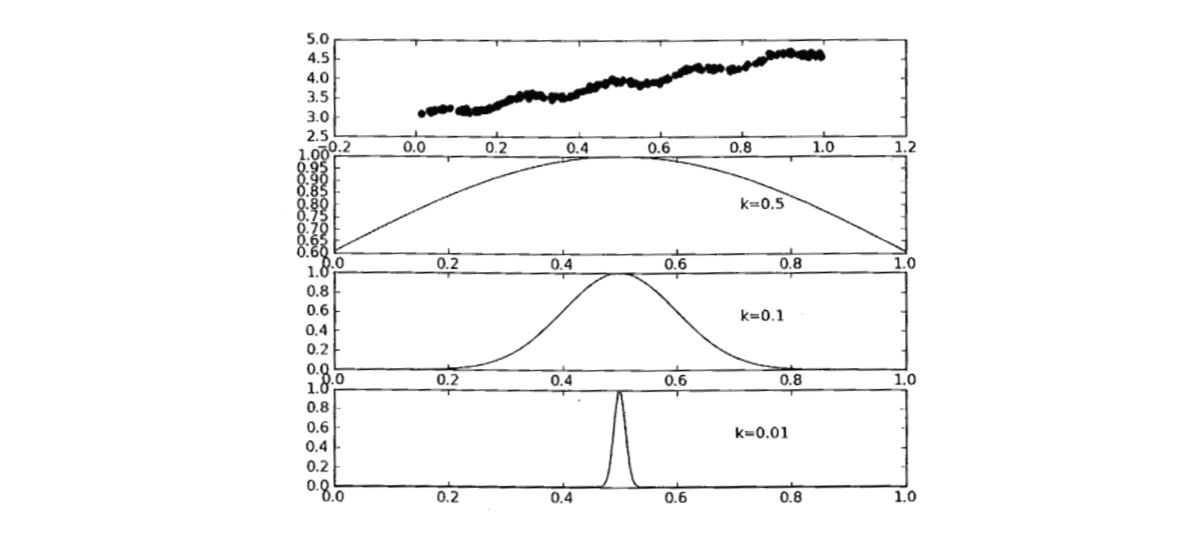
这样就构建了一个只含有对角元素的权重矩阵$\omega$,并且点$x$与$x_i$越近,$w(i,i)$将会越大。上述公式包含一个需要用户指定的参数k,它决定了对附近的点赋予多大的权重,这也是使用局部线性加权回归时唯一需要考虑的参数,在下图中可以看到参数$k$与权重的关系。(实际应用中k可以通过K折交叉验证确定)
1 def lwlr(testPoint, xArr, yArr, k=1.0): 2 xMat = mat(xArr); yMat = mat(yArr).T 3 m = shape(xMat)[0] 4 weights = mat(eye((m))) 5 for j in range(m): 6 diffMat = testPoint - xMat[j, :] 7 weights[j, j] = exp(diffMat * diffMat.T / (-2.0 * k ** 2.0)) 8 xTx = xMat.T * (weights * xMat) 9 if linalg.det(xTx) == 0.0: 10 print("This matrix is singular, cannot do inverse") 11 return 12 ws = xTx.I * (xMat.T * (weights * yMat)) 13 return testPoint * ws 14 15 def lwlrTest(testArr, xArr, yArr, k=1.0): 16 m = shape(testArr)[0] 17 yHat = zeros(m) 18 for i in range(m): 19 yHat[i] = lwlr(testArr[i], xArr, yArr, k) 20 return yHat
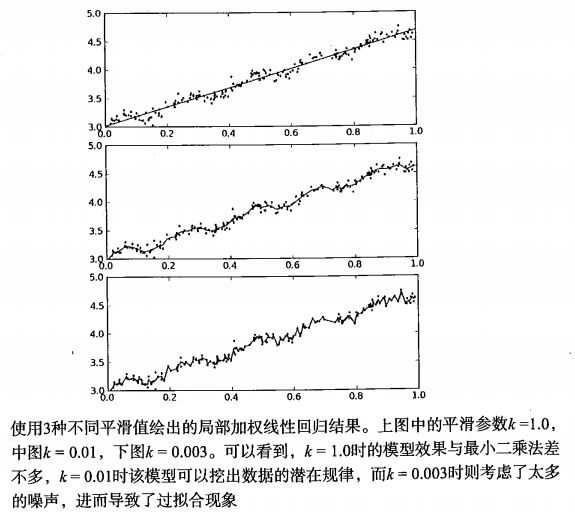
原文:https://www.cnblogs.com/ningjing213/p/13724386.html