在计算理论中,确定有限状态自动机或确定有限自动机(英语:deterministic finite automaton, DFA)是一个能实现状态转移的自动机。对于一个给定的属于该自动机的状态和一个属于该自动机字母表Σ的字符,它都能根据事先给定的转移函数转移到下一个状态(这个状态可以是先前那个状态)。
可以通过建立状态机来解决问题。
每次输入都会引起状态的改变或者不变。再次输入一个值,状态又会改变。
我们把所有状态罗列出来,每次输入都改变他的状态。如果最后的状态是合法的,那么证明这个输入符合条件。
相应的数学建模中也用到类似的算法思想,解决商人过河问题、人狼羊菜过河问题,以及操作系统中也有涉猎,输出进程安全序列也是类似的思想
DFA是一个由五元组定义的数学模型:M=(S,∑,δ,s0,F)
(2)S是一个有穷状态集合
(3)∑是一个有穷的输入字母表
(4)δ是状态转换函数,是SX∑->S上的单值部分映射,δ(s,a)=s‘(s∈S,s‘∈S)
(5)s0是唯一初态
(6)F是终态集合,F是S的子集
M = ( S,Σ ,δ,s0,F )
(1) S:有穷状态集
(2)Σ:输入符号集合,即输入字母表。假设ε 不是Σ中的元素
(3)δ:将S×Σ映射到2S的转换函数。?s∈S, a∈Σ, δ(s,a)表示从状态s出发,沿着标记为a的边所能到达的状态集合
(4)s0:开始状态 (或初始状态),s0∈S
(5)F:接收状态(或终止状态)集合,F? S
dfa和nfa的区别
| NFA | DFA | |
| 初始状态 | 不唯一 | 唯一 |
| 弧上的标记 | 字(单字符字/ε) | 字符(串) |
| 转换关系 | 非确定 | 确定 |
两个DFA的等价指的是对任何两个DFA,M和M‘,如果L(M)=L(M‘),则称两者是等价的
思路:DFA的每一个状态对应于NFA的一组状态,用DFA的一个状态去记录NFA输入一个符号后可能达到的状态集合
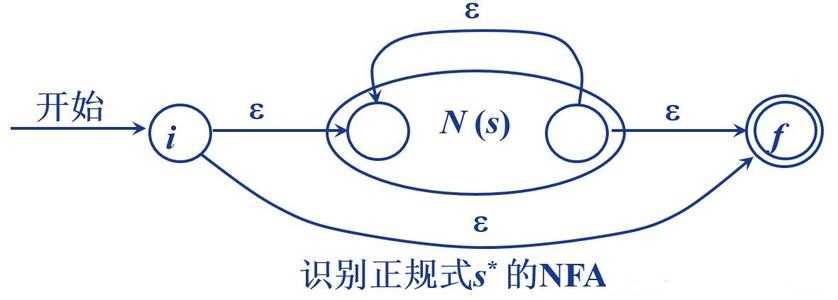
(1)状态集合I的闭包ε-Closure(I),定义
(2)状态集合I的a弧转换表示为Ia,Ia=ε-Closure(move(I,a))
对于给定的DFA M,寻找一个状态数比M小的DFA M‘使得L(M)=L(M‘)
1.状态的等价性:
假设s和t为M的两个状态(终态和非终态)
①若分别从状态s和状态t出发都能读出某个字α而停止于终态,则称s和t等价
②存在一个字α,使得s和t一个读出α停止于终态,另一个读出α停止于非终态,则称s和t可区别
2.基本思想:
①把M的状态集分为一些不相交的子集,使任何两个不同子集状态是可区别的,而同一子集的任何两个状态是等价的
②让每个子集选出一个代表,同时消去其他状态
3.划分
①把S划分为终态和非终态两个子集,形成基本划分∏
②假定某个时候∏已含m个子集,记为∏={I(1),I(2),…,I(m)},检查∏中的每个子集能否进一步划分:
(a)假定s1和s2是I(i)={s1,s2,…sk}中的两个状态,它们经过a弧分别到达t1和t2,而t1和t2属于现行∏中的两个不同子集,则s1和s2不等价
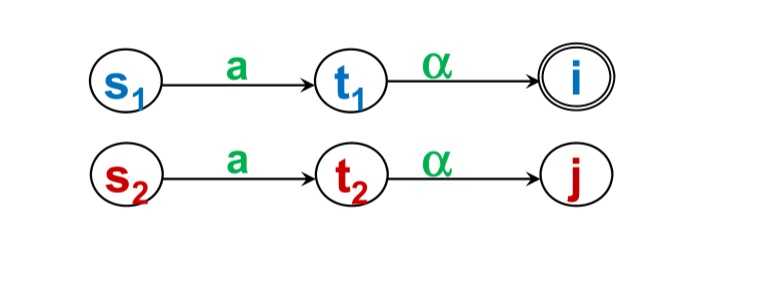
(b)一般地,对于某个I(i),若Ia(i)落于现行∏中N个不同的子集,则应把I(i)划分成N个不相交的组
例:


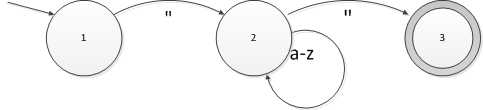
语言 L = { a } { a , b } ? ( { ? } ∪ ( { . , _ } { a , b } { a , b } ? ) ) L=\{a\}\{a,b\}^*(\{\epsilon \} \cup (\{.,\_\}\{a,b\}\{a,b\}^*))L={a}{a,b}?({?}∪({.,_}{a,b}{a,b}?))
这个语言是指,由a开头,后接任意长度的a、b串,然后再接空串(代表结束)。或者是接以.或_开头的,后接长度大于等于1的a、b串。
正则表达式(Regular Expression, RE)是一种用来描述正则语言的更紧凑的表示方法。
以上面的语言举例,写成正则表达式则可表示成:r = a ( a ∣ b ) ? ( ? ∣ ( . ∣ ) ( a ∣ b ) ( a ∣ b ) ? ) r=a(a|b)^*(\epsilon | (.|_)(a|b)(a|b)^*)r=a(a∣b)?(?∣(.∣)?(a∣b)(a∣b)?)
正则表达式可以由较小的正则表达式按照特定规则递归地构建。每个正则表达式r定义一个语言。记为L(r)。这个语言也是根据r的子表达式所表示的语言递归定义的。
r和s都是RE,表示的语言分别是L(r)和L(s),则
rs(r连接s)是一个RE,L ( r ∣ s ) = L ( r ) L ( s ) L(r|s) = L(r)L(s)L(r∣s)=L(r)L(s)注:运算的优先级:*、连接、|
例:∑ = { a , b } \sum = \{a,b\}∑={a,b},则
注:可以用RE定义的语言叫做正则语言(regular language)或正则集合(regular set)。
| 定律 | 描述 |
|---|---|
| r | s = s | r | | 是可以交换的 |
| r | (s | t) = (r | s) | t | | 是可以结合的 |
| r ( s t ) = ( r s ) t | 连接是可以结合的 |
| r (s | t) = rs | rt | 连接对 | 是可分配的 |
| ? r = r ? = r \epsilon r = r \epsilon = r?r=r?=r | ? \epsilon?是连接的单位元 |
| $r^* = (r | \epsilon)^*$ |
| r ? ? = r ? r^{**} = r^*r??=r? | *具有幂等性 |
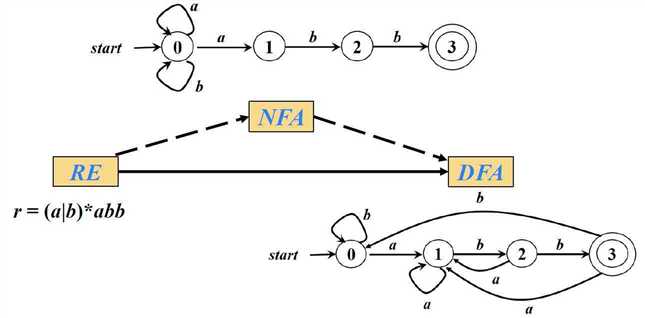
G,存在定义同一语言的正则表达式rr,存在生成同一语言的正则文法G正则表达式构造NFA在转化为DFA[正则表达式][有限状态机DFA][不确定的有限状态机NFA]
原文:https://www.cnblogs.com/Carraway-Space/p/13727250.html