【模拟费用流·总结篇】抛开模型看模拟费用流的本质

\(Preface\)

模拟费用流是一个非常巧妙的算法，余之前也对其进行了许多研究，但一直没有触碰到它的本质：模拟费用流，自然就是在费用流的基础上模拟。

因此呐，这次余找到一道比较好也比较有难度的例题，来进行一次模拟费用流算法的巩固深化复习。

前置知识

• 【模拟费用流·入门篇】由兔子和洞谈起的模拟费用流常规模型
• 【模拟费用流·进阶篇】继兔子和洞而论的模拟费用流进阶模型

[NOI2019] 序列

• 给定两个长度为\(n\)的整数序列\(\{a_i\},\{b_i\}\)。
• 要求在两个序列中分别选出恰好\(K\)个数，其中至少有\(L\)对数下标相同。
• 求出数的总和的最大值。
• 数据总数\(\le10\)，\(\sum n\le10^6\)，\(1\le L\le K\le n\le 2\times 10^5\)，\(1\le a_i,b_i\le10^9\)

费用流

考虑暴力费用流，建图如下：

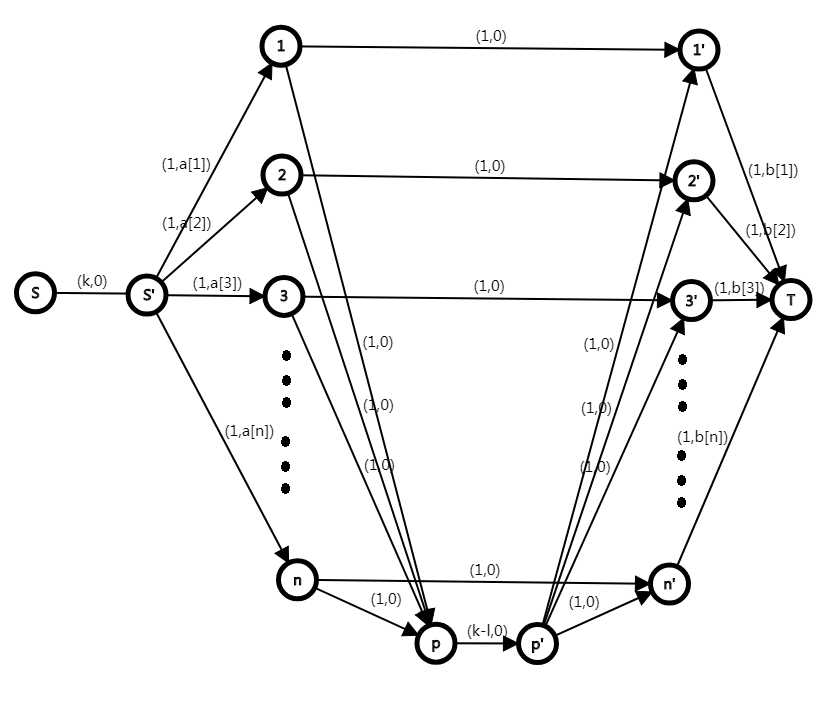
解释：一般的边对应选出一对下标相同的数的情况。由于能任选\(k-l\)对，因此任选边\(p\rightarrow p‘\)的流量是\(k-l\)。

然而直接跑费用流显然是无法通过此题的。

模拟费用流

模拟费用流是对费用流的模拟，接下来的每种情况其实都在费用流的图中有着对应的流法（于括号中给出）。

考虑\(p\rightarrow p‘\)肯定是最优的边，因此先贪心将其流满。

具体地，对两个序列各自开一个堆，每次选出还未选择过的\(a\)中最大元素\(a_u\)和\(b\)中最大元素\(b_v\)，将总流量\(k\)以及\(p\rightarrow p‘\)的容量减\(1\)。

（\(S\rightarrow S‘\rightarrow u\rightarrow p\rightarrow p‘\rightarrow v‘\rightarrow T\)）

然而如果\(b_u\)或者\(a_v\)已经被选择过了，那么就可以让它们不流\(p\rightarrow p‘\)这条任选边，而是从一般的边上走，此时可以将\(p\rightarrow p‘\)的容量加\(1\)。

（\(S\rightarrow S‘\rightarrow u\rightarrow u‘\rightarrow T\)或\(S\rightarrow S‘\rightarrow v\rightarrow v‘\rightarrow T\)）

流满了\(p\rightarrow p‘\)，接下来有\(3\)种选择：

• 选择一对都未选过的\(a_x,b_x\)。（\(S\rightarrow S‘\rightarrow x\rightarrow x‘\rightarrow T\)）
• 选择一个最大的\(a_u\)，以及一个最大的\(a_v\)已经被选过的\(b_v\)。相当于将原先与\(a_v\)通过任选边连接的\(b\)转送给\(a_u\)，而\(a_v\)和\(b_v\)自己走一般边（但要注意如果\(b_u\)也已经被选过了，需要将\(p\rightarrow p‘\)容量加\(1\)重新执行一开始的操作）。（\(S\rightarrow S‘\rightarrow u\rightarrow p\leftarrow v\rightarrow v‘\rightarrow T\)，其中左箭头表示走反向边，即退流操作）
• 选择一个最大的\(b_v\)，以及一个最大的\(b_u\)已经被选过的\(a_u\)。同上。

具体实现也就是开五个堆，分别存储剩余的最大的\(a_u\)、剩余的最大的\(b_v\)、最大的\(b_u\)已经被选过的\(a_u\)、最大的\(a_v\)已经被选过的\(b_v\)、都未选过的\(a_x,b_x\)。

\(Postscript\)

至此，终于可以对模拟费用流算法进行一次总结了：

• 模拟费用流的本质，是在费用流的基础上模拟。（所以不会费用流一切都白搭）
• 模拟费用流的核心，是贪心。（说实话很多模拟费用流题目反而是利用费用流去证明贪心的正确性）
• 模拟费用流的实现，通常会用到堆。
• 模拟费用流的题目，大都非常玄学。（废话）

咳咳，这就是余目前能想到的有关模拟费用流的全部内容啦！

【模拟费用流·总结篇】抛开模型看模拟费用流的本质

原文：https://www.cnblogs.com/Nero-Claudius/p/Simulation_of_CostFlow3.html