测试使用K-最近邻（kNN）算法的30个问题

作者|SUNIL RAY
编译|Flin
来源|analyticsvidhya

介绍

如果你要问我机器学习中2种最直观的算法——那就是k最近邻（kNN）和基于树的算法。两者都易于理解，易于解释，并且很容易向人们展示。有趣的是，上个月我们对这两种算法进行了技能测试。

如果你不熟悉机器学习，请确保在了解这两种算法的基础上进行测试。它们虽然简单，但是功能强大，并且在工业中得到广泛使用。此技能测试将帮助你在k最近邻算法上进行自我测试。它是专为你测试有关kNN及其应用程序的知识而设计的。

超过650人注册了该测试。如果你是错过这项技能测试的人之一，那么这篇文章是测试问题和解决方案。这是参加考试的参与者的排行榜。

• https://datahack.analyticsvidhya.com/contest/skilltest-k-nearest-neighbor-knn/#LeaderBoard

有用的资源

这里有一些资源可以深入了解该主题。

• 机器学习算法的基本知识（带有Python和R代码）：R语言进行Logistic回归的简单指南
  • https://www.analyticsvidhya.com/blog/2017/09/common-machine-learning-algorithms/
• K-最近邻（kNN）算法
  • https://www.analyticsvidhya.com/blog/2018/03/introduction-k-neighbours-algorithm-clustering/

技能测试问答

1） k-NN算法在测试时间而不是训练时间上进行了更多的计算。

A）真
B）假

解决方案：A

该算法的训练阶段仅包括存储训练样本的特征向量和类别标签。

在测试阶段，通过分配最接近该查询点的k个训练样本中最频繁使用的标签来对测试点进行分类——因此需要更高的计算量。

2）假设你使用的算法是k最近邻算法，在下面的图像中，____将是k的最佳值。

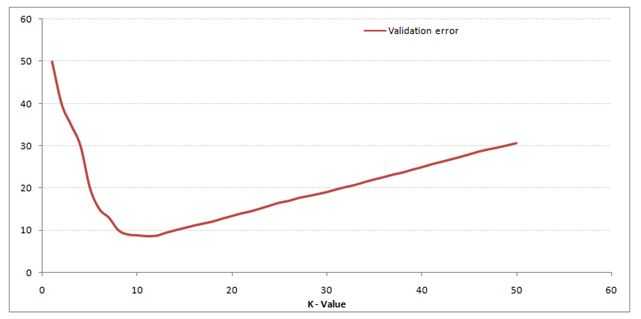
A） 3
B） 10
C） 20
D） 50
解决方案：B

当k的值为10时，验证误差最小。

3）在k-NN中不能使用以下哪个距离度量？

A) Manhattan
B) Minkowski
C) Tanimoto
D) Jaccard
E) Mahalanobis
F）都可以使用

解决方案：F

所有这些距离度量都可以用作k-NN的距离度量。

4）关于k-NN算法，以下哪个选项是正确的？

A）可用于分类
B）可用于回归
C）可用于分类和回归

解决方案：C

我们还可以将k-NN用于回归问题。在这种情况下，预测可以基于k个最相似实例的均值或中位数。

5）关于k-NN算法，以下哪个陈述是正确的？

1. 如果所有数据的比例均相同，则k-NN的效果会更好
2. k-NN在少数输入变量（p）下工作良好，但在输入数量很大时会遇到困难
3. k-NN对所解决问题的函数形式没有任何假设

A）1和2
B）1和3
C）仅1
D）以上所有

解决方案：D

以上陈述是kNN算法的假设

6）下列哪种机器学习算法可用于估算分类变量和连续变量的缺失值？

A）K-NN
B）线性回归
C）Logistic回归

解决方案：A

k-NN算法可用于估算分类变量和连续变量的缺失值。

7）关于曼哈顿距离，以下哪项是正确的？

A）可用于连续变量
B）可用于分类变量
C）可用于分类变量和连续变量
D）无

解决方案：A

曼哈顿距离是为计算实际值特征之间的距离而设计的。

8）对于k-NN中的分类变量，我们使用以下哪个距离度量？

1. 汉明距离
2. 欧氏距离
3. 曼哈顿距离

A）1
B）2
C）3
D）1和2
E）2和3
F）1,2和3

解决方案：A

在连续变量的情况下使用欧氏距离和曼哈顿距离，而在分类变量的情况下使用汉明距离。

9）以下哪个是两个数据点A（1,3）和B（2,3）之间的欧几里得距离？

A）1
B）2
C）4
D）8

解决方案：A

sqrt（（1-2）^ 2 +（3-3）^ 2）= sqrt（1 ^ 2 + 0 ^ 2）= 1

10）以下哪个是两个数据点A（1,3）和B（2,3）之间的曼哈顿距离？

A）1
B）2
C）4
D）8

解决方案：A

sqrt（mod（（1-2））+ mod（（3-3）））= sqrt（1 + 0）= 1

内容：11-12

假设你给出了以下数据，其中x和y是2个输入变量，而Class是因变量。

以下是散点图，显示了2D空间中的上述数据。

11）假设你要使用3-NN中的欧氏距离来预测新数据点x = 1和y = 1的类别。该数据点属于哪个类别？

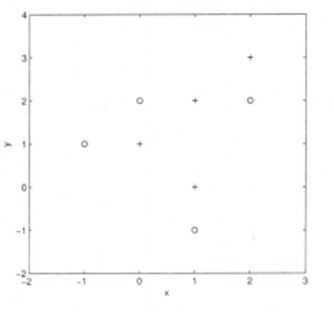
A）+ 类
B）– 类
C）不能判断
D）这些都不是

解决方案：A

所有三个最近点均为 + 类，因此此点将归为+ 类。

12）在上一个问题中，你现在要使用7-NN而不是3-KNN，以下x = 1和y = 1属于哪一个？

A）+ 类
B）– 类

C）不能判断

解决方案：B

现在，此点将归类为 – 类，因为在最近的圆圈中有4个 – 类点和3个 + 类点。

内容13-14：

假设你提供了以下2类数据，其中“+”代表正类，“-”代表负类。

13）k-NN中k的以下哪个k值会最小化留一法交叉验证的准确性？

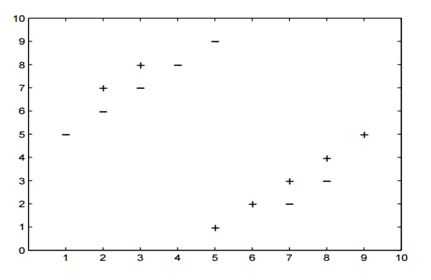
A）3
B）5
C）两者都相同
D）没有一个

解决方案：B

5-NN将至少留下一个交叉验证错误。

14）以下哪一项是k = 5时不进行交叉验证的准确性？

A）2/14
B）4/14
C）6/14
D）8/14
E）以上都不是

解决方案：E

在5-NN中，我们将有10/14的交叉验证精度。

15）关于k-NN中的k，根据偏差，以下哪一项是正确的？

A）当你增加k时，偏差会增加
B）当你减少k时，偏差会增加
C）不能判断
D）这些都不是

解决方案：A

大K表示简单模型，简单模型始终被视为高偏差

16）关于方差k-NN中的k，以下哪一项是正确的？

A）当你增加k时，方差会增加
B）当你减少k时，方差会增加
C）不能判断
D）这些都不是

解决方案：B

简单模型将被视为方差较小模型

17）以下两个距离（欧几里得距离和曼哈顿距离）已经给出，我们通常在K-NN算法中使用这两个距离。这些距离在点A（x1，y1）和点B（x2，Y2）之间。

你的任务是通过查看以下两个图形来标记两个距离。关于下图，以下哪个选项是正确的？

A）左为曼哈顿距离，右为欧几里得距离
B）左为欧几里得距离，右为曼哈顿距离
C）左或右都不是曼哈顿距离
D）左或右都不是欧几里得距离
解决方案：B

左图是欧几里得距离的工作原理，右图是曼哈顿距离。

18）当你在数据中发现噪声时，你将在k-NN中考虑以下哪个选项？

A）我将增加k的值
B）我将减少k的值
C）噪声不能取决于k
D）这些都不是

解决方案：A

为了确保你进行的分类，你可以尝试增加k的值。

19）在k-NN中，由于维数的存在，很可能过度拟合。你将考虑使用以下哪个选项来解决此问题？

1. 降维
2. 特征选择

A）1
B）2
C）1和2
D）这些都不是

解决方案：C

在这种情况下，你可以使用降维算法或特征选择算法

20）以下是两个陈述。以下两个陈述中哪一项是正确的？

1. k-NN是一种基于记忆的方法，即分类器会在我们收集新的训练数据时立即进行调整。
2. 在最坏的情况下，新样本分类的计算复杂度随着训练数据集中样本数量的增加而线性增加。

A）1
B）2
C）1和2
D）这些都不是

解决方案：C

21）假设你给出了以下图像（左1，中2和右3），现在你的任务是在每个图像中找出k-NN的k值，其中k1代表第1个图，k2代表第2个图，k3是第3个图。

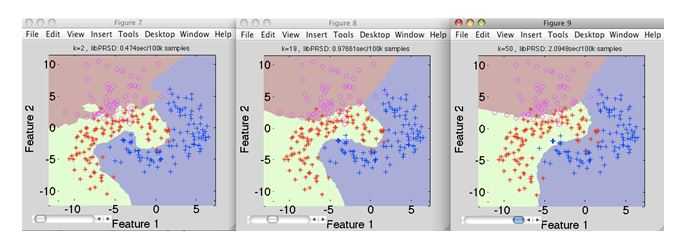
A）k1 > k2 > k3
B）k1 < k2
C）k1 = k2 = k3
D）这些都不是

解决方案：D

k值在k3中最高，而在k1中则最低

22）在下图中，下列哪一个k值可以给出最低的留一法交叉验证精度？

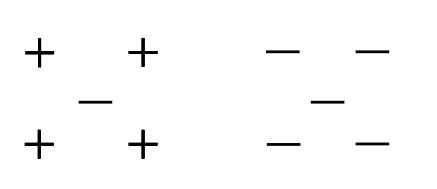
A）1
B）2
C）3
D）5
解决方案：B

如果将k的值保持为2，则交叉验证的准确性最低。你可以自己尝试。

23）一家公司建立了一个kNN分类器，该分类器在训练数据上获得100％的准确性。当他们在客户端上部署此模型时，发现该模型根本不准确。以下哪项可能出错了？

注意：模型已成功部署，除了模型性能外，在客户端没有发现任何技术问题

A）可能是模型过拟合
B）可能是模型未拟合
C）不能判断
D）这些都不是

解决方案：A

在一个过拟合的模块中，它似乎会在训练数据上表现良好，但它还不够普遍，无法在新数据上给出相同的结果。

24）你给出了以下2条语句，发现在k-NN情况下哪个选项是正确的？

1. 如果k的值非常大，我们可以将其他类别的点包括到邻域中。
2. 如果k的值太小，该算法会对噪声非常敏感

A）1
B）2
C）1和2
D）这些都不是

解决方案：C

这两个选项都是正确的，并且都是不言而喻的。

25）对于k-NN分类器，以下哪个陈述是正确的？

A） k值越大，分类精度越好

B） k值越小，决策边界越光滑

C） 决策边界是线性的

D） k-NN不需要显式的训练步骤

解决方案：D

选项A：并非总是如此。你必须确保k的值不要太高或太低。

选项B：此陈述不正确。决策边界可能有些参差不齐

选项C：与选项B相同

选项D：此说法正确

26）判断题：可以使用1-NN分类器构造2-NN分类器吗？

A）真
B）假

解决方案：A

你可以通过组合1-NN分类器来实现2-NN分类器

27）在k-NN中，增加/减少k值会发生什么？

A） K值越大，边界越光滑

B） 随着K值的减小，边界变得更平滑

C） 边界的光滑性与K值无关

D） 这些都不是

解决方案：A

通过增加K的值，决策边界将变得更平滑

28）以下是针对k-NN算法给出的两条陈述，其中哪一条是真的？

1. 我们可以借助交叉验证来选择k的最优值
2. 欧氏距离对每个特征一视同仁

A）1
B）2
C）1和2
D）这些都不是

解决方案：C

两种说法都是正确的

内容29-30：假设你已经训练了一个k-NN模型，现在你想要对测试数据进行预测。在获得预测之前，假设你要计算k-NN用于预测测试数据类别的时间。

注意：计算两个观测值之间的距离将花费时间D。

29）如果测试数据中有N（非常大）的观测值，则1-NN将花费多少时间？

A）N * D
B）N * D * 2
C）（N * D）/ 2
D）这些都不是

解决方案：A

N的值非常大，因此选项A是正确的

30）1-NN，2-NN，3-NN所花费的时间之间是什么关系。

A）1-NN > 2-NN > 3-NN
B）1-NN < 2-NN < 3-NN
C）1-NN ~ 2-NN ~ 3-NN
D）这些都不是

解决方案：C

在kNN算法中，任何k值的训练时间都是相同的。

总体分布

以下是参与者的分数分布：

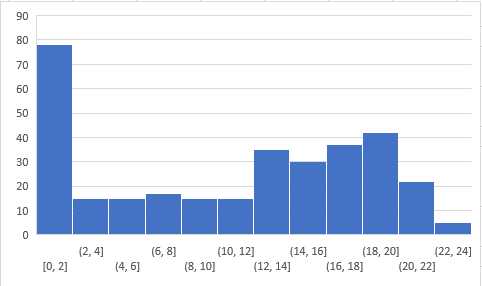
你可以在此处（https://datahack.analyticsvidhya.com/contest/skilltest-logistics-regression/#LeaderBoard） 访问分数。超过250人参加了技能测试，获得的最高分是24。

原文链接：https://www.analyticsvidhya.com/blog/2017/09/30-questions-test-k-nearest-neighbors-algorithm/

欢迎关注磐创AI博客站：
http://panchuang.net/

sklearn机器学习中文官方文档：
http://sklearn123.com/

欢迎关注磐创博客资源汇总站：
http://docs.panchuang.net/

测试使用K-最近邻（kNN）算法的30个问题

原文：https://www.cnblogs.com/panchuangai/p/13733044.html