1.黄金分割点是把一条线段分割成两个部分,使得一部分与全长之比等于另一部分与这一部分之比,取其前三位的近似值大概是0.618。
2.斐波那契数列{1,1,2,3,5,8,13,...}两个相邻数的比例无限接近0.618
1.斐波那契思想与二分法相类似,不过中间点不再是中点,而变成了黄金分割点的附近mid=low+F(k-1)-1,F代表斐波那契数列
对于F(k-1)-1的含义的理解
1.F代表的斐波那契数列
2.k代表斐波那契数列的第k个元素
3.由F[k]=F[k-1]+F[k-2]可以得知,可以得到F[k]-1=(F[k-1]-1)+(F[k-2]-1)+1,这个式子说明只要是顺序表的长度为F[k]-1,就可以分为(F[k-1]-1)和(F[k-2]-1)两段,另外一个1就是
mid位置的元素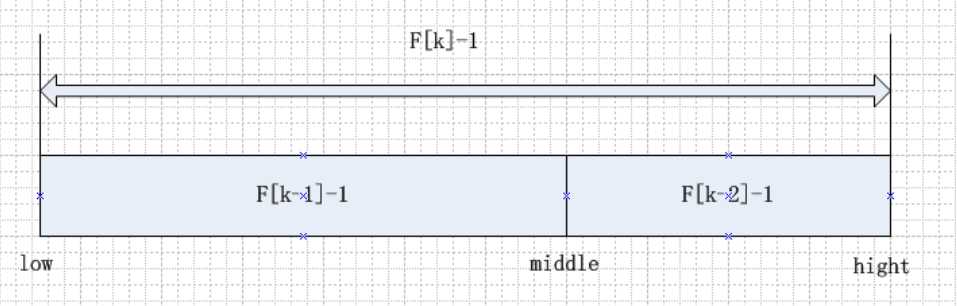
4.类似的每一个子段也可以用同样的方式来进行分隔
5.但是顺序表的长度不一定是恰好等于F[k]-1,所以需要将原来的顺序表的长度增加到F[k]-1,这里的k值仅仅需要恰好使得F[k]-1恰好大于或者等于n,新增位置,都赋值为下标为n-1位置的值就可以了
package com.cai.math; import java.util.Arrays; /** * 斐波那契查找方法的实现 * 前提:查找数组是一个有序的数组 */ public class FibonacciSearch { static int maxSize = 20; public static void main(String[] args) { int[] arr ={1,3,5,7,22,33,45}; System.out.println(sort(arr,22)); } /** * 创建一个 斐波那契数组 * @return */ public static int[] createFib(){ int[] fib = new int[maxSize]; fib[0] = 1; fib[1] = 1; for (int i = 2; i < maxSize; i++) { fib[i] = fib[i-1] + fib[i-2]; } return fib; } /** * 查找 * @param arr * @param value 需要查找的值 * @return 查找到值所在的下角标 */ public static int sort(int[] arr ,int value){ int low = 0; int high = arr.length -1; int k = 0; //表示斐波那契分割值的下角标 int[] fib = createFib(); while (high > fib[k]-1){ k++; } //因为f[k]这个值可能大于数组a的长度,因此需要使用Arrays类,构造一个新的数组并指向a int[] temp= Arrays.copyOf(arr, fib[k]);//不足的部分会使用0填充 //用数组的最后一个数来填充 for(int i=high+1;i<temp.length;i++) { temp[i]=arr[high]; } while(low<=high) { int mid=low+fib[k-1]-1; //求分割中值得公式 if(value<temp[mid]) {//应当向前面进行查找 high=mid-1; k--;//全部元素=前面的元素+后面的元素 //f[k]=f[k-1]+f[k-2] //因为前面有f[k-1]个元素所以可以继续拆分分配f[k-1]=f[k-2]+f[k-3] //即f[k-1]的前面继续查找k-- //下次训话mid=f[k-1-1]-1 } else if(value>temp[mid]) {//后面查找,右边查找 low=mid+1; k-=2; //f[k]=f[k-1]+f[k-2] 长度分成的第二部分 } else { if(mid<=high) { //主要判断是否是临时数组的补量部分 return mid; } else { return high; } } } return -1; } }
原文:https://www.cnblogs.com/cai170221/p/13737832.html