以[1,3,8,17,5,14,10]为例，首先我们需要开设一个栈S保存，栈中的元素S[i]代表了以S[i]结尾的长度为i+1的最长上升子序列的最小取值（0<=i）。
然后执行下列算法步骤：
（图片来源：小象学院）
得到的栈的大小即是最长上升子序列的长度，需要值得注意的是栈里面的元素并不一定是真正的最长子序列的所有元素。
演示：假设已经遍历到17了
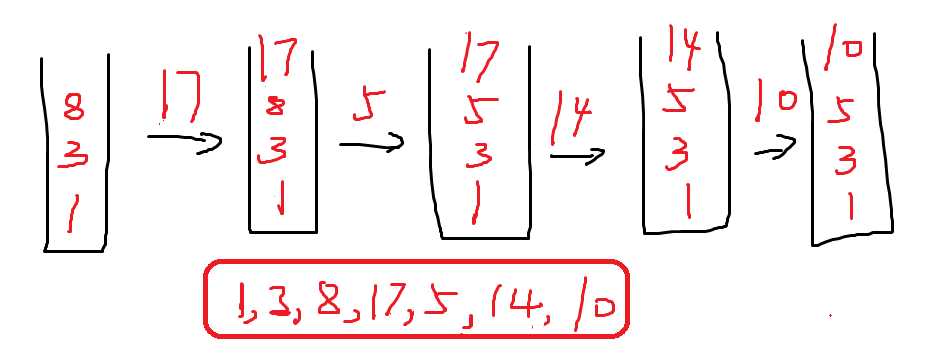
不难发现，最长上升子序列长度为4，并且结尾最小的数为10，而且栈中的元素并不一定是真正的子序列，因为（1,3,8,10）同样也是最长的上升子序列。
该算法借用了类似贪心的思想，通过维护栈中的元素，通过元素的个数来计算最长上升子序列的长度，非常的巧妙。
时间复杂度计算：遍历数组为O(n)的复杂度，对于每个元素，我们可以在栈中利用二分查找获得下标，因此整体的时间复杂度为O(n*logn)。
原文：https://www.cnblogs.com/ISGuXing/p/13741534.html