In linear algebra, the restricted isometry property (RIP) characterizes matrices which are nearly orthonormal, at least when operating on sparse vectors. The concept was introduced by Emmanuel Candès and Terence Tao[1] and is used to prove many theorems in the field of compressed sensing.[2] There are no known large matrices with bounded restricted isometry constants (computing these constants is strongly NP-hard,[3] and is hard to approximate as well[4]), but many random matrices have been shown to remain bounded. In particular, it has been shown that with exponentially high probability, random Gaussian, Bernoulli, and partial Fourier matrices satisfy the RIP with number of measurements nearly linear in the sparsity level.[5] The current smallest upper bounds for any large rectangular matrices are for those of Gaussian matrices.[6] Web forms to evaluate bounds for the Gaussian ensemble are available at the Edinburgh Compressed Sensing RIC page.[7]
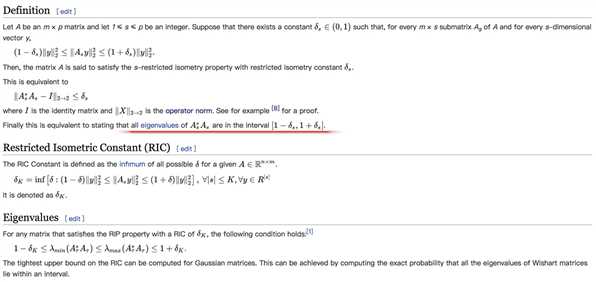
Definition[edit]
Let A be an m × p matrix and let 1 ≤ s ≤ p be an integer. Suppose that there exists a constant {\displaystyle \delta _{s}\in (0,1)}
such that, for every m × s submatrix As of A and for every s-dimensional vector y,
- {\displaystyle (1-\delta _{s})\|y\|_{2}^{2}\leq \|A_{s}y\|_{2}^{2}\leq (1+\delta _{s})\|y\|_{2}^{2}.\,}
Then, the matrix A is said to satisfy the s-restricted isometry property with restricted isometry constant {\displaystyle \delta _{s}}
.
This is equivalent to
- {\displaystyle \|A_{s}^{*}A_{s}-I\|_{2\to 2}\leq \delta _{s}}
where {\displaystyle I}
is the identity matrix and {\displaystyle \|X\|_{2\to 2}}
is the operator norm. See for example [8] for a proof.
Finally this is equivalent to stating that all eigenvalues of {\displaystyle A_{s}^{*}A_{s}}
are in the interval {\displaystyle [1-\delta _{s},1+\delta _{s}]}
.
Restricted Isometric Constant (RIC)[edit]
The RIC Constant is defined as the infimum of all possible {\displaystyle \delta }
for a given {\displaystyle A\in \mathbb {R} ^{n\times m}}
.
- {\displaystyle \delta _{K}=\inf \left[\delta :(1-\delta )\|y\|_{2}^{2}\leq \|A_{s}y\|_{2}^{2}\leq (1+\delta )\|y\|_{2}^{2}\right],\ \forall |s|\leq K,\forall y\in R^{|s|}}
It is denoted as {\displaystyle \delta _{K}}
.
Eigenvalues[edit]
For any matrix that satisfies the RIP property with a RIC of {\displaystyle \delta _{K}}, the following condition holds:[1]
- {\displaystyle 1-\delta _{K}\leq \lambda _{min}(A_{\tau }^{*}A_{\tau })\leq \lambda _{max}(A_{\tau }^{*}A_{\tau })\leq 1+\delta _{K}}
.
The tightest upper bound on the RIC can be computed for Gaussian matrices. This can be achieved by computing the exact probability that all the eigenvalues of Wishart matrices lie within an interval.
See also[edit]
- Compressed sensing
- Mutual coherence (linear algebra)
- Terence Tao‘s website on compressed sensing lists several related conditions, such as the ‘Exact reconstruction principle‘ (ERP) and ‘Uniform uncertainty principle‘ (UUP)[9]
- Nullspace property, another sufficient condition for sparse recovery
- Generalized restricted isometry property,[10] a generalized sufficient condition for sparse recovery, where mutual coherence and restricted isometry property are both its special forms.
References[edit]
- ^ Jump up to:a b E. J. Candes and T. Tao, "Decoding by Linear Programming," IEEE Trans. Inf. Th., 51(12): 4203–4215 (2005).
- ^ E. J. Candes, J. K. Romberg, and T. Tao, "Stable Signal Recovery from Incomplete and Inaccurate Measurements," Communications on Pure and Applied Mathematics, Vol. LIX, 1207–1223 (2006).
- ^ A. M. Tillmann and M. E. Pfetsch, "The Computational Complexity of the Restricted Isometry Property, the Nullspace Property, and Related Concepts in Compressed Sensing," IEEE Trans. Inf. Th., 60(2): 1248–1259 (2014)
- ^ Abhiram Natarajan and Yi Wu, "Computational Complexity of Certifying Restricted Isometry Property," Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques (APPROX/RANDOM 2014) (2014)
- ^ F. Yang, S. Wang, and C. Deng, "Compressive sensing of image reconstruction using multi-wavelet transform", IEEE 2010
- ^ B. Bah and J. Tanner "Improved Bounds on Restricted Isometry Constants for Gaussian Matrices"
- ^ "Archived copy". Archived from the original on 2010-04-27. Retrieved 2010-03-31.
- ^ "A Mathematical Introduction to Compressive Sensing" (PDF). Cis.pku.edu.cn. Retrieved 15 May 2018.
- ^ "Compressed sensing". Math.ucla.edu. Retrieved 15 May 2018.
- ^ Yu Wang, Jinshan Zeng, Zhimin Peng, Xiangyu Chang and Zongben Xu (2015). "On Linear Convergence of Adaptively Iterative Thresholding Algorithms for Compressed Sensing". IEEE Transactions on Signal Processing. 63 (11): 2957–2971. arXiv:1408.6890. doi:10.1109/TSP.2015.2412915.
