原题:http://poj.org/problem?id=1182
参考题解:https://blog.csdn.net/niushuai666/article/details/6981689
Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 119629 Accepted: 36539 Description
动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。A吃B, B吃C,C吃A。
现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述:
第一种说法是"1 X Y",表示X和Y是同类。
第二种说法是"2 X Y",表示X吃Y。
此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
你的任务是根据给定的N(1 <= N <= 50,000)和K句话(0 <= K <= 100,000),输出假话的总数。Input
第一行是两个整数N和K,以一个空格分隔。
以下K行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中D表示说法的种类。
若D=1,则表示X和Y是同类。
若D=2,则表示X吃Y。Output
只有一个整数,表示假话的数目。Sample Input
100 7 1 101 1 2 1 2 2 2 3 2 3 3 1 1 3 2 3 1 1 5 5Sample Output
3
带关系域的并查集
我们用变量re记录对应结点和其父结点的关系。
* 如果re==0 说明当前和fa是同类
* 如果re==1 说明当前被fa吃
* 如果re==2 说明当前吃fa
然后在并查集找最终父结点的过程中更新结点关系。
更新结点时结点关系变化的规律?:
我们可以先从三个结点a, b, c开始考虑。
假设c是b的父结点,a是b的子节点。现在要更新a父结点为c。求a结点和c结点的关系。
情况如下图
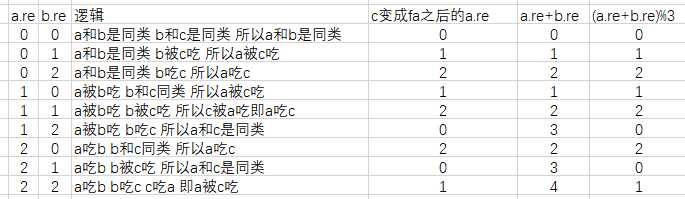
在更新的时候,我们只需要按照上表“c变成fa之后的a.re”的内容来更新数据就可以了。其中我们可以发现这个结果为(a.re+b.re)%3。
此段代码为:
1 ll findFather(ll id, ll &totres){//带更新关系域的的找父亲 2 if(nos[id].fa==id) return id; 3 ll fa=findFather(nos[id].fa, totres); 4 totres+=nos[id].re;//累加当前结点以及当前结点之前的re 5 nos[id].re=totres%3;//更新关系域 6 nos[id].fa=fa;//更新父结点 7 return fa; 8 }
插入结点时结点关系变化的规律?
假设题目现在给出x和y一对关系式,x和y的父结点分别为fax和fay。插入结点时的操作为让fay的父结点变成fax。求fay和fax之间的关系。
情况如下图
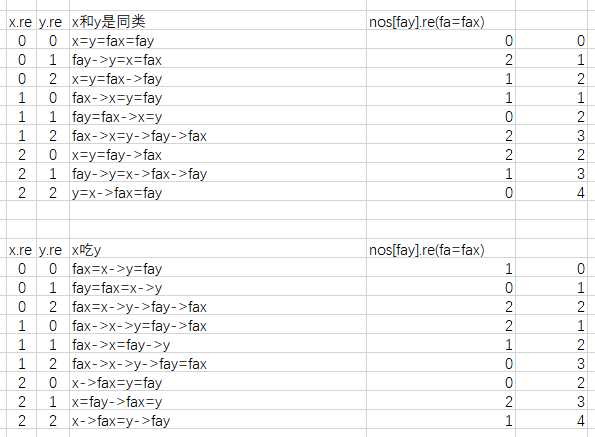
按这个表进行插入新结点的re赋值操作。
此段代码为:
1 nos[fay].fa=fax; 2 if(1==d){//x和y是同类 3 if(nos[x].re==0){ 4 if(nos[y].re==0) nos[fay].re=0; 5 else if(nos[y].re==1) nos[fay].re=2; 6 else if(nos[y].re==2) nos[fay].re=1; 7 } 8 else if(nos[x].re==1){ 9 if(nos[y].re==0) nos[fay].re=1; 10 else if(nos[y].re==1) nos[fay].re=0; 11 else if(nos[y].re==2) nos[fay].re=2; 12 } 13 else if(nos[x].re==2){ 14 if(nos[y].re==0) nos[fay].re=2; 15 else if(nos[y].re==1) nos[fay].re=1; 16 else if(nos[y].re==2) nos[fay].re=0; 17 } 18 } 19 else if(2==d){//x吃y 20 if(nos[x].re==0){ 21 if(nos[y].re==0) nos[fay].re=1; 22 else if(nos[y].re==1) nos[fay].re=0; 23 else if(nos[y].re==2) nos[fay].re=2; 24 } 25 else if(nos[x].re==1){ 26 if(nos[y].re==0) nos[fay].re=2; 27 else if(nos[y].re==1) nos[fay].re=1; 28 else if(nos[y].re==2) nos[fay].re=0; 29 } 30 else if(nos[x].re==2){ 31 if(nos[y].re==0) nos[fay].re=0; 32 else if(nos[y].re==1) nos[fay].re=2; 33 else if(nos[y].re==2) nos[fay].re=1; 34 } 35 }
如何判断题目给出的x和y关系与之前的内容矛盾?
如果x和y的父结点fax和fay不同,那么说明在之前x和y之间没有任何关系。因此题目给出任何x和y的关系都是不矛盾的。所以我们只考虑x和y的父结点相同的情况。
如果题目给出的d==1,即x和y为同类, 因为fax==fay,那么x和y必然re相同。
如果题目给出的d==2,即x吃y,那么x和y和祖先lca有且仅有三种情况
* 情况1:lca->x->y->lca 那么x.re=1 y.re=2
* 情况2:->x(lca)->y-> 那么x.re=0 y.re=1
* 情况3:->x->y(lca)-> 那么x.re=2 y.re=0
只要满足其中任意一种情况,那么就不矛盾。
此段代码为:
1 ll fax=findFather(x, totx); 2 ll fay=findFather(y, toty); 3 if(fax==fay){//只有当lca相同时才有可能有冲突 并且不需要更新关系 因为关系已知 4 if(1==d){//同类re应该相同 5 if(nos[x].re!=nos[y].re) 6 res++; 7 } 8 else if(2==d){//x吃y 9 /* 10 * 情况1:lca->x->y->lca 11 * 情况2:->x(lca)->y-> 12 * 情况3:->x->y(lca)-> 13 */ 14 bool con1=false, con2=false, con3=false; 15 if(nos[x].re==1&&nos[y].re==2) con1=true; 16 if(nos[x].re==0&&nos[y].re==1) con2=true; 17 if(nos[x].re==2&&nos[y].re==0) con3=true; 18 if ((!con1) && (!con2) && (!con3)) { 19 res++; 20 } 21 } 22 continue;; 23 }
全部代码:
1 #include "iostream" 2 #include "stdio.h" 3 using namespace std; 4 typedef long long ll; 5 const ll mx=5e4+10; 6 ll N, K; 7 8 typedef struct NODE{ 9 ll re;//关系域 10 /* 11 * 如果re==0 说明当前和fa是同类 12 * 如果re==1 说明当前被fa吃 13 * 如果re==2 说明当前吃fa 14 */ 15 ll fa;//父亲 16 }NODE; 17 NODE nos[mx]; 18 19 ll findFather(ll id, ll &totres){//带更新关系域的的找父亲 20 if(nos[id].fa==id) return id; 21 ll fa=findFather(nos[id].fa, totres); 22 totres+=nos[id].re;//累加当前结点以及当前结点之前的re 23 nos[id].re=totres%3;//更新关系域 24 nos[id].fa=fa;//更新父结点 25 return fa; 26 } 27 void init(){ 28 for(ll i=1;i<=N;i++){ 29 nos[i].re=0; 30 nos[i].fa=i; 31 } 32 } 33 int main() { 34 ll res=0; 35 scanf("%lld %lld", &N, &K); 36 init(); 37 for(ll i=1;i<=K;i++){ 38 ll d, x, y, totx=0, toty=0; 39 scanf("%lld %lld %lld", &d, &x, &y); 40 if(x>N||y>N){//当前的话中X或Y比N大,就是假话; 41 res++; 42 continue;; 43 } 44 if(x==y&&2==d){//当前的话表示X吃X,就是假话。 45 res++; 46 continue; 47 } 48 ll fax=findFather(x, totx); 49 ll fay=findFather(y, toty); 50 if(fax==fay){//只有当lca相同时才有可能有冲突 并且不需要更新关系 因为关系已知 51 if(1==d){//同类re应该相同 52 if(nos[x].re!=nos[y].re) 53 res++; 54 } 55 else if(2==d){//x吃y 56 /* 57 * 情况1:lca->x->y->lca 58 * 情况2:->x(lca)->y-> 59 * 情况3:->x->y(lca)-> 60 */ 61 bool con1=false, con2=false, con3=false; 62 if(nos[x].re==1&&nos[y].re==2) con1=true; 63 if(nos[x].re==0&&nos[y].re==1) con2=true; 64 if(nos[x].re==2&&nos[y].re==0) con3=true; 65 if ((!con1) && (!con2) && (!con3)) { 66 res++; 67 } 68 } 69 continue;; 70 } 71 //lca不同时 加入并查集 72 nos[fay].fa=fax; 73 if(1==d){//x和y是同类 74 if(nos[x].re==0){ 75 if(nos[y].re==0) nos[fay].re=0; 76 else if(nos[y].re==1) nos[fay].re=2; 77 else if(nos[y].re==2) nos[fay].re=1; 78 } 79 else if(nos[x].re==1){ 80 if(nos[y].re==0) nos[fay].re=1; 81 else if(nos[y].re==1) nos[fay].re=0; 82 else if(nos[y].re==2) nos[fay].re=2; 83 } 84 else if(nos[x].re==2){ 85 if(nos[y].re==0) nos[fay].re=2; 86 else if(nos[y].re==1) nos[fay].re=1; 87 else if(nos[y].re==2) nos[fay].re=0; 88 } 89 } 90 else if(2==d){//x吃y 91 if(nos[x].re==0){ 92 if(nos[y].re==0) nos[fay].re=1; 93 else if(nos[y].re==1) nos[fay].re=0; 94 else if(nos[y].re==2) nos[fay].re=2; 95 } 96 else if(nos[x].re==1){ 97 if(nos[y].re==0) nos[fay].re=2; 98 else if(nos[y].re==1) nos[fay].re=1; 99 else if(nos[y].re==2) nos[fay].re=0; 100 } 101 else if(nos[x].re==2){ 102 if(nos[y].re==0) nos[fay].re=0; 103 else if(nos[y].re==1) nos[fay].re=2; 104 else if(nos[y].re==2) nos[fay].re=1; 105 } 106 } 107 } 108 cout<<res<<endl; 109 return 0; 110 }
原文:https://www.cnblogs.com/sloth612/p/13721192.html