Linear Block Codes
Linear block codes are the most important and widely used class of block codes. A
block code is linear if any linear combination of two codewords is a codeword. In the
binary case, this means that the sum of any two codewords is a codeword. In linear
block codes the codewords form a k-dimensional subspace of an n-dimensional space.
Linear block codes are described in terms of a generator matrix G, which is a k x n
binary matrix such that each codeword c can be written in the form

where u is the binary data sequence of length k (the encoder input). Obviously, the
all-0 sequence of length n is always a codeword of an ( n, k) linear block code.

Matlab Coding


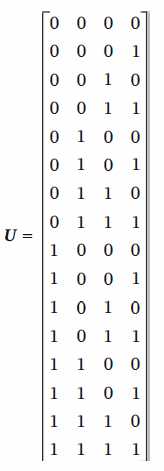
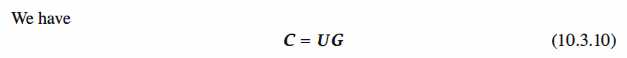


% MATLAB script for Illustrative Problem 10.8. % Generate U, denoting all information sequences. k=4; for i=1:2^k for j=k:-1:1 if rem(i-1,2^(-j+k+1))>=2^(-j+k) u(i,j)=1; else u(i,j)=0; end echo off ; end end echo on ; % Define G, the generator matrix. g=[1 0 0 1 1 1 0 1 1 1; 1 1 1 0 0 0 1 1 1 0; 0 1 1 0 1 1 0 1 0 1; 1 1 0 1 1 1 1 0 0 1]; % Generate codewords. c=rem(u*g,2); % Find the minimum distance. w_min=min(sum((c(2:2^k,:))‘));
>> w_min
w_min =
2
>> c
c =
0 0 0 0 0 0 0 0 0 0
1 1 0 1 1 1 1 0 0 1
0 1 1 0 1 1 0 1 0 1
1 0 1 1 0 0 1 1 0 0
1 1 1 0 0 0 1 1 1 0
0 0 1 1 1 1 0 1 1 1
1 0 0 0 1 1 1 0 1 1
0 1 0 1 0 0 0 0 1 0
1 0 0 1 1 1 0 1 1 1
0 1 0 0 0 0 1 1 1 0
1 1 1 1 0 0 0 0 1 0
0 0 1 0 1 1 1 0 1 1
0 1 1 1 1 1 1 0 0 1
1 0 1 0 0 0 0 0 0 0
0 0 0 1 0 0 1 1 0 0
1 1 0 0 1 1 0 1 0 1
>> u
u =
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
>> g
g =
1 0 0 1 1 1 0 1 1 1
1 1 1 0 0 0 1 1 1 0
0 1 1 0 1 1 0 1 0 1
1 1 0 1 1 1 1 0 0 1
In a systematic code, the first k binary symbols in a codeword are the information bits, and the
remaining n - k binary symbols are the parity-check symbols.

Reference,
1. <<Contemporary Communication System using MATLAB>> - John G. Proakis
CCS - Channel Capacity and Coding - Channel Coding - Linear Block Codes
原文:https://www.cnblogs.com/zzyzz/p/13759217.html