求树的直径的方法:
求树的直径的bfs/dfs方法的正确性证明:
问题就在第一点:距离x最远的y点在树的直径上。
现在证明这个结论
反正法:
假设y不在直径上,那么有以下情况:
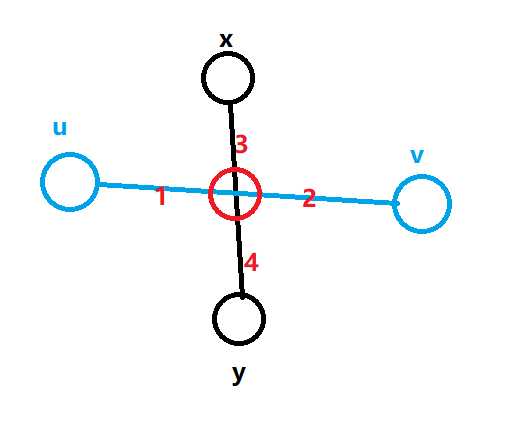
? 此时\(u -> v\)为树的直径
? 而\(dist(x, y) \ge dist(x, u)\)它们存在公共部分\(3\), 所以有\(1 \le 4\)
? 从而\(1 + 2 \le 4 + 2\), 所以有\(dist(u, v) \le dist(y, v)\)
? 那么\(dist(y, v)\)就成了直径,\(y\)成了直径的端点,与假设矛盾。
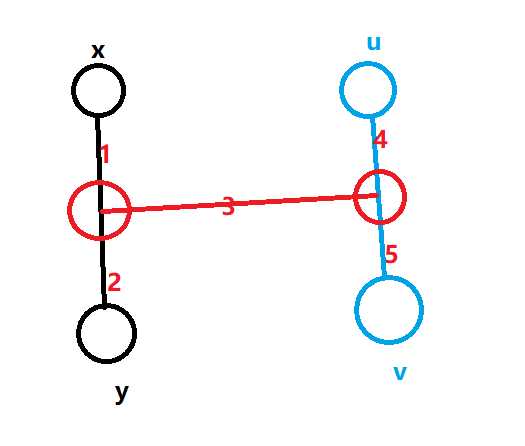
? 此时\(u -> v\)
为树的直径
? 因为\(dist(x, y) \ge dist(x, v)\)
? 所以有\(1 + 3 + 5 \le 1 + 2\)
? \(\to 3 + 5 \le 2\)
? \(\to 2 + 3 \ge 5\)
? \(\to 2 + 3 + 4 \ge 5 + 4\)
? \(\to dist(y, u) \ge dist(u, v)\)
? 所以\(dist(y, u)\)为树的直径,所以\(y\)为树的直径上的端点,与假设矛盾。
综上,结论“距离x最远的y点在树的直径上”结论获证。
原文:https://www.cnblogs.com/tomori/p/13759042.html