在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小(magnitude)和方向的量。 ————百度百科
读者:笔者你好水啊
笔者:没办法吖笔者懒(:≡
在一个直角三角形中:
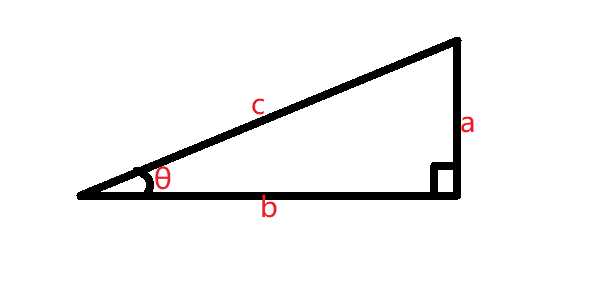
\(sin\theta=\frac{a}{c}\)
\(cos\theta=\frac{b}{c}\)
由此我们可以得到以下结论:
\(sin^2\theta+cos^2\theta=1\)
证明:
\(sin^2\theta+cos^2\theta=(\frac{a}{c})^2+(\frac{b}{c})^2=\frac{a^2}{c^2}+\frac{b^2}{c^2}=\frac{a^2+b^2}{c^2}=1\)
最后为什么是直接是1?
\(a^2+b^2=c^2\)
传说中的勾股定理呢~
\(\vec V_1 \cdot \vec V_2 = \vert V_1 \vert \cdot \vert V_2 \vert \cdot cos\theta = x_1 \cdot x_2 + y_1 \cdot y_2\)
由此可以得出:
\(cos\theta = \frac{x_1 \cdot x_2 + y_1 \cdot y_2}{\vert V_1 \vert \cdot \vert V_2 \vert}\)
\(\vec V_1 \times \vec V_2 = \vert V_1 \vert \cdot \vert V_2 \vert \cdot sin\theta = x_1 \cdot y_2 - y_1 \cdot x_2\)
\(\vert \frac{x_1 \cdot y_2 - y_1 \cdot x_2}{\sqrt{(X_1)^2+(y_1)^2}} \vert\)
--The End
哇笔者太弱了写不出来证明过程所以就抄上了
笔者要回去补向量了
原文:https://www.cnblogs.com/w-rb/p/13760163.html