10.2 考试总结

10.2 Noip 模拟赛总结

T1 旅行：

给你一个长度为 \(n\) 的序列 \(a\), 设一个区间的最大值为 \(x\), 最小值为 \(y\) ,且该区间的左右端点为 \(l,r\) .

定义一个区间的价值为 \(x-y \over{r-l}\) ，让你求价值最大的区间。

对于 40% 的数据， \(n\leq 1000\).

对于 90% 的数据 , \(n\leq 10^5\)

对于 100% 的数据 \(n\leq 10^7\)

题解

part1 40分

按照题意模拟就行。

part2 90分

我们有个结论：最大值和最小值一定在区间的边界上。

很好证明，随着区间长度的增大，区间最大值和最小值不会改变，但区间长度变大，也就是分母变大了，值也就会减少。

这里口胡一下 二分的做法。假设我们二分出来的答案为 \(mid\)

则有 \({x-y \over{r-l}} = mid\)

移项可得： \(x-y = mid \times (r-l)\)

即： \(x + mid \times l = y + mid \times r\)

随便维护一下就行 （其实是我不会写）。

part3 100分

这需要一定的转化。

我们可以把 \((i,a_i)\) 看做平面上的一个点，问题就可以转化为求两点之间斜率的绝对值的最大值。

直接 O(n) 的维护一下凸包就可以 （然鹅我不会）。

还有一种简单的方法，但需要用到一个结论：我们只需要算出相邻两个点之间的斜率就可以得出最后的答案。

简单证明一下，假设有 \(A,B,C\) 三个相邻的点，我们要选的是 \(A,C\) 这两个点。

• 假设 \(B\) 在 \(AC\) 的连线上，那么结果不会改变。
• 如果 \(B\) 在 \(AC\) 的连线的上方，则选 \(AB\) 会更优。
• 同理在 \(AC\) 连线下方，选 \(BC\) 会更优。

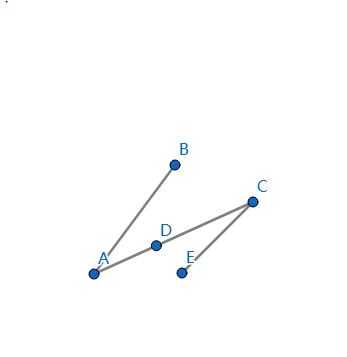
\(D,B,E\) 三个点分别对应上面三种情况。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int inf = 2147483647;
int T,n,ans,a[1000010];
inline int read()
{
	int s = 0,w = 1; char ch = getchar();
	while(ch < ‘0‘ || ch > ‘9‘){if(ch == ‘-‘) w = -1; ch = getchar();}
	while(ch >= ‘0‘ && ch <= ‘9‘){s = s * 10 + ch - ‘0‘; ch = getchar();}
	return s * w;
}
signed main()
{
	freopen("travel.in","r",stdin);
	freopen("travel.out","w",stdout);
	T = read();
	while(T--)
	{
		n = read(); ans = -inf;
		for(int i = 1; i <= n; i++) a[i] = read();
		for(int i = 2; i <= n; i++)
		{
			ans = max(ans,abs(a[i]-a[i-1]));
		}
		printf("%lld\n",ans);
	}
	fclose(stdin); fclose(stdout);
	return 0;
}

10.2 考试总结

原文：https://www.cnblogs.com/genshy/p/13762153.html