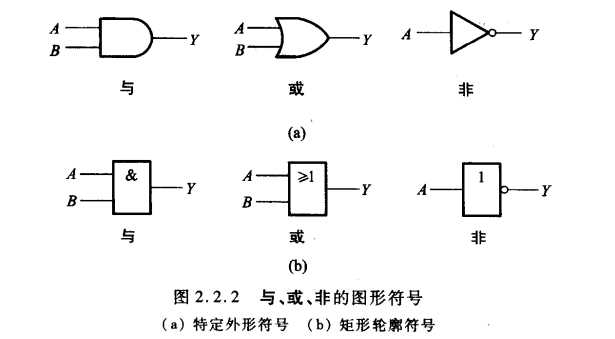
与、或、非
复合逻辑运算最常见的有与非、或非、与或非、异或、同或等。
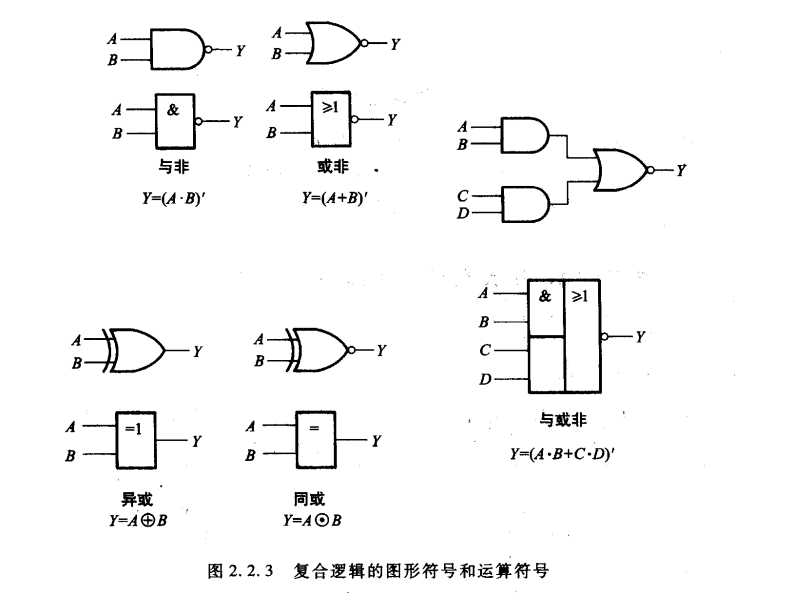
异或:\(A \bigoplus B = AB‘+A‘B\)
同或:\(A \bigodot B = AB+A‘B‘\)
异或与同或互为反运算。
也叫布尔恒等式(证明方法包括真值表法和推演法):
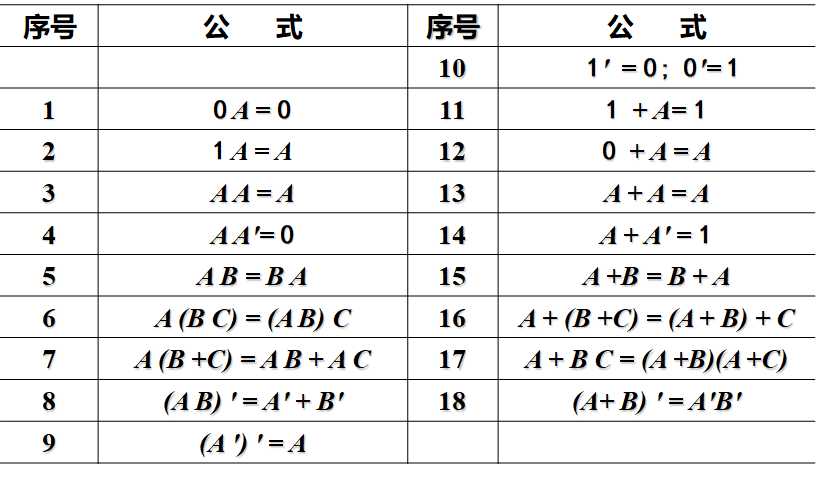
总结为以下几类:
开始为0行
由基本公式导出,便于化简逻辑函数。
两个乘积项相加时,若一项以另一项为因子,则该项多余:
\(A+AB =A\)
两个乘积项相加时,一项取反后是另一项的因子,则此因子多余,可以消去:
\(A+A‘B=A+B\)
两个乘积项相加时,若他们分别包含\(B\)和\(B‘\)两个因子而其他因子相同,则两项可合并。
\(AB+AB‘=A\)
变量\(A\)和包含\(A\)的和相乘时,结果为\(A\):
\(A(A+B)=A\)
若两个乘积项中分别包含\(A\)和\(A‘\)两个因子,则其余因子组成第三个乘积项时,第三个乘积项是多余的:
\(AB+A‘C+BC=AB+A‘C\)
进一步
\(AB+A‘C+BCD=AB+A‘C\)
\(A\)和一个乘积项的非相乘,且\(A\)为这个乘积项的因子时,\(A\)这个因子可以消去:
\(A(AB)‘=AB‘\)
\(A‘\)和一个乘积项的非相乘,且\(A\)为这个乘积项的因子时,结果等于\(A‘\)
\(A‘(AB)‘=A‘\)
在任何一个包含A的逻辑等式中,若以另外一个逻辑式代入式中所有A的位置,则等式依然成立。
对于任意一个逻辑式\(Y\),若将其中所有的“\(\cdot\)”换成“\(+\)”,“\(+\)”换成“\(\cdot\)”,\(0\)换成\(1\),\(1\)换成\(0\),原变量换成反变量,反变量换成原变量,则得到的结果就是\(Y‘\)。这个规律称为反演定理。
反演定理为求取已知逻辑式的反逻辑式提供了方便。
在使用反演定理时,还需注意遵守以下两个规则:
①仍需遵守“先括号、然后乘、最后加”的运算优先次序。
②不属于单个变量上的反号应保留不变。

若两逻辑式相等,则它们的对偶式也相等,这就是对偶定理。
所谓对偶式是这样定义的:对于任何一个逻辑式\(Y\),若将其中的"\(\cdot\)"换成"\(+\)","\(+\)"换成"\(\cdot\)",0换成1,1换成0,则得到一个新的逻辑式\(Y\),这个\(Y^D\)就称为\(Y\)的对偶式,或者说\(Y\)和\(Y^D\)互为对偶式.
\(Y=F(A,B,C,...)\)
逻辑真值表、逻辑表达式、逻辑图、波形图
①找出真值表中使逻辑函数Y=1的那些输人变量取值的组合。
②每组输入变量取值的组合对应一个乘积项,其中取值为1的写入原变量,取值为0的写入反变量。
③将这些乘积项相加,即得Y的逻辑函数式。
从给定的逻辑函数式转换为相应的逻辑图时,只要用逻辑图形符号代替逻辑函数式中的逻辑运算符号并按运算优先顺序将它们连接起来,就可以得到所求的逻辑图了。
而在从给定的逻辑图转换为对应的逻辑函数式时,只要从逻辑图的输人端到输出端逐级写出每个图形符号的输出逻辑式,就可以在输出端得到所求的逻辑函数式了。
波形图可以很方便地与真值表转换。不再介绍。
在n变量逻辑函数中,若m为包含n个因子的乘积项,而且这n个变量均以原变量或反变量的形式在m中出现一次,则称m为该组变量的最小项。 n变量的最小项有\(2^n\)个。
从最小项的定义出发可以证明它具有如下的重要性质:
①在输人变量的任何取值下必有一个最小项,而且仅有一个最小项的值为1。
②全体最小项之和为1。
③任意两个最小项的乘积为0。
④具有相邻性的两个最小项之和可以合并成一项并消去一对因子。
在n变量逻辑函数中,若M为n个变量之和,而且这n个变量均以原变量或反变量的形式在M中出现一次,则称M为该组变量的最大项。 n变量的最大项数目和最小项数目是相等的,\(2^n\)项。
根据最大项的定义同样也可以得到它的主要性质,这就是:
①在输人变量的任何取值下必有一个最大项,而且只有一个最大项的值为0。
②全体最大项之积为0。
③任意两个最大项之和为1。
④只有一个变量不同的两个最大项的乘积等于各相同变量之和。
首先将给定的逻辑函数式化为若干乘积项之和的形式(亦称“积之和”形式),然后再利用基本公式A+A‘=1将每个乘积项中缺少的因子补全,这样就可以将与或的形式化为最小项之和的标准形式。
写成“和的积”,利用AA‘=0
没有看到好的方法。。
在与或逻辑函数式中,若其中包含的乘积项已经最少,而且每个乘积项里的因子也不能再减少时,则称此逻辑函数式为最简形式。对与或逻辑式最简形式的定义对其他形式的逻辑式同样也适用,即函数式中相加的乘积项不能再减少,而且每项中相乘的因子不能再减少时,则函数式为最简形式。
没有固定的步骤。常利用的公式:
\(AB+AB‘=A\)
\(A+AB=A\)
\(AB+A‘C+BC=AB+A‘C\) 和 \(AB+A‘C+BCD=AB+A‘C\)
\(A+A‘B=A+B\)
\(A+A=A\) 重复写入某一项,获取更加简单的化简结果
\(A+A‘=1\) 某一项乘以\((A+A‘=1)\),拆成两项与其他项合并。
将n变量的全部最小项各用一个小方块表示,并使具有逻辑相邻性的最小项在几何位置上也相邻排列,所得到的图形称为n变量最小项的卡诺图。
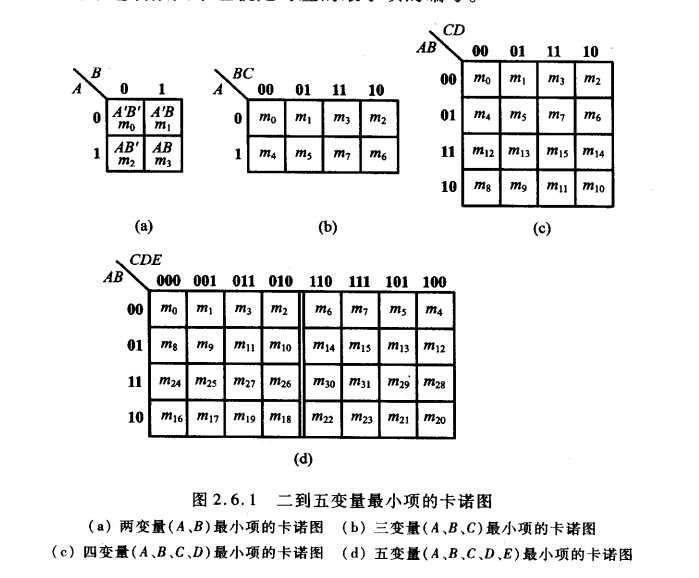
用卡诺图表示一个逻辑函数:首先将逻辑函数化为最小项之和的形式,然后在卡诺图上与这些最小项对应的位置上填人1,在其余的位置上填人0,就得到了表示该逻辑函数的卡诺图。
化简原理:相邻性的最小项可以合并,并消去不同的因子。由于在卡诺图上几何位置相邻与逻辑上的相邻性是一致的,所以可以直观地找出那些具有相邻性的最小项将其合并化简。
在看哪些是可以消去因子的时候,找其01均有出现的。
2.卡诺图化简法的步骤
用卡诺图化简逻辑函数时可按如下步骤进行:
(1)将函数化为最小项之和的形式。
(2)画出表示该逻辑函数的卡诺图。
(3)找出可以合并的最小项。
(4)选取化简后的乘积项。选取的原则是:
①这些乘积项应包含函数式中所有的最小项(应复盖卡诺图中所有的1)。(可以多次覆盖 A+A=A)
②所用的乘积项数目最少。也就是可合并的最小项组成的矩形组数目最少。
③每个乘积项包含的因子最少。也就是每个可合并的最小项矩形组中应包含尽量多的最小项。
注意:对于不是完整的最小项而言,只需要关注已有的因子。
也可以找0再取反。
圈出的矩形要覆盖所有的1且最少(最少乘积项)最大(乘积项最少因子)。
约束项:不会出现的值,都使其对应的最小项恒等于0.比如000不能出现,则\(A‘B‘C‘=0\),\(A‘B‘C‘\)即是一个约束项。
由于约束项的值恒等于0,所以逻辑函数式中可以写也可以不写。
任意项:输入变量的某些取值下,函数值是1还是0皆可,并不影响电路的功能。再这些变量取值下,其值等于1的那些最小项称为任意项。(这个在具体的场景下才会用到?不太理解。
加入无关项应与函数式中尽可能多的最小项具有逻辑相邻性。
在卡诺图中,无关项对应的位置添x(无限可能)。
原文:https://www.cnblogs.com/TeaWithCola/p/Basic_Logic_Algebra.html