在具体实现这些问题的时候,主要是依据该文章的思路来。
背包问题是泛指以下这一种问题:
给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。是一个典型的多阶段决策的过程,适用于动态规划来解决。
\(01\)背包指的是每一种物品只有一件,可以选择放或者不放。
【问题描述】
一个旅行者有一个最多能装\(M\) 公斤的背包,现在有\(n\) 件物品,它们的重量分别是\(W_1\),\(W_2,…,W_n\),它们的价值分别为\(C_1,C_2,…,C_n\),求旅行者能获得最大总价值。
【输入】
第一行:两个整数,\(M\)(背包容量,\(M ≤ 200\))和\(N\)(物品数量,\(N ≤ 30\));
第\(2…N+1\)行:每行二个整数\(W_i,C_i\),表示每个物品的重量和价值。
【输出】
仅一行,一个数,表示最大总价值。
【样例输入】
10 4
2 1
3 3
4 5
7 9
【样例输出】
12
这是最基础的背包问题,其基本特点是,每种物品仅有一件按,可以选择放或者不放。
根据这一特点,可以定义这样一个状态,\(d[i] [j]\) 表示从前i件物品中选择容量不超过j的,可以获得的最大价值。根据每一件物品可以选择放或者不放,状态转移方程可以这样表示:
\(d[i] [j] = max ( d[i-1] [j], d[i-1] [j - w[i]] + v[i] )\)
上面这个方程是背包问题的基础方程,几乎其他的背包问题都是由上述方程演变而来。上述方程的含义为,考虑当前的物品放或者不放,如果不放进背包,那么问题可以转换为从\(i-1\)件物品中放入容量为\(j\)的背包,即\(d[i] [j] = d[i-1] [j]\),如果放进背包,那么问题转换为从前\(i-1\)件物品中选择放入容量为\(j - w[i]\)的背包中,此时的最大价值就是\(d[i-1] [j - w[i]]\)在加上放入第\(i\)件物品的价值\(v[i]\)。
如果还是不理解可以参照下方表格
| N/W | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 |
| 3 | 0 | 1 | 3 | 5 | 5 | 6 | 8 | 8 | 9 | 9 |
| 4 | 0 | 1 | 3 | 5 | 5 | 6 | 9 | 9 | 10 | 12 |
参考程序:
#include <iostream>
#define T 1005
#define M 105
using namespace std;
int main () {
ios::sync_with_stdio(0);
int s, n, t[M], v[M], d[M][T] = {0};
cin >> s >> n;
for (int i = 1; i <= n; i++)
cin >> t[i] >> v[i];
for (int i = 1; i <= n; i++)
for (int j = 0; j <= s; j++)
if (j >= t[i])
d[i][j] = max (d[i-1][j], d[i-1][j-t[i]] + v[i]);
else
d[i][j] = d[i-1][j];
cout << d[n][s];
return 0;
}
空间优化:
上面算法的时间和空间复杂度为\(O(NV)\),其中时间复杂度基本不能继续优化了,但是可以考虑优化空间,复杂度可以达到\(O(V)\)。
由上述的递推公式可以得出,\(d[i] [j]\)只和\(d[i-1] [j]\) 和 \(d[i-1] [j - w[i]]\)有关,即只和\(i-1\)时刻的状态有关。
那么是否可以省略第一个维度,只用一维数组来考虑,同时又要求填充这个一维数组时,始终保证当前的\(i\)只和\(i-1\)时刻有关?
实际上是可以的,\(d[j] = max(d[j], d[j - w[i]] + v[i])\),实际上相当于\(d[i] [j] = max ( d[i-1] [j], d[i-1] [j - w[i]] + v[i] )\),但是其中的j的变化必须是逆序推导从总的容量\(W\)开始变化到\(w[i]\)。这样才能保证\(d[j - w[i]]\) 等价于 \(d[i-1] [j - w[i]]\)(\(i\)只会被\(i-1\)的状态影响)。如果是顺序推导,那么可能会\(d[i] [j]\)从\(d[i] [j - w[i]]\)推得(\(i\)会被\(i\)的状态影响),不符合要求。
还是通过一个表格来理解
从后往前推导:
| 更新次数/W | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 第1次更新 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 第2次更新 | 4 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 1 | 0 |
| 第3次更新 | 9 | 9 | 8 | 8 | 6 | 5 | 5 | 3 | 1 | 0 |
| 第4次更新 | 12 | 10 | 9 | 9 | 6 | 5 | 5 | 3 | 1 | 0 |
如果更够跟着表格进行一次推导,那么就能明白为什么要逆推了,再来看顺推(根据程序手动模拟,只需要推导一次的更新就明白为什么顺推是错的)
| 更新次数/W | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 第1次更新 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 |
从\(d[4]\)开始,就走向了错误的方向。第一个物品的重量为\(2\),价值为\(1\),那么\(d[4] = d[4-2] + 1 = 2\),我们要求当前状态只和\(i-1\)前一次有关,而\(d\)的更新是基于当前状态\(i\)下更新的,\(d\)会慢慢叠加越来越大。因此是顺推是错误的。
参考程序
#include <iostream>
#define T 1005
#define M 105
using namespace std;
int main () {
ios::sync_with_stdio(0);
int s, n, t[M], v[M], d[T] = {0};
cin >> s >> n;
for (int i = 1; i <= n; i++)
cin >> t[i] >> v[i];
for (int i = 1; i <= n; i++) {
for (int j = s; j >= t[i]; j --)
d[j] = max (d[j], d[j-t[i]]+v[i]);
}
cout << d[s];
return 0;
}
【问题描述】
设有\(n\)种物品,每种物品有一个重量及一个价值。但每种物品的数量是无限的,同时有一个背包,最大载重量为\(M\),今从\(n\)种物品中选取若干件(同一种物品可以多次选取),使其重量的和小于等于\(M\),而价值的和为最大。
【输入】
第一行:两个整数,\(M\)(背包容量,\(M <= 200\))和\(N\)(物品数量,\(N <= 30\));
第\(2…N+1\)行:每行二个整数\(W_i,C_i\),表示每个物品的重量和价值。
【输出】
仅一行,一个数,表示最大总价值。
【样例输入】
10 4
2 1
3 3
4 5
7 9
【样例输出】
12
和刚才的\(01\)背包不同的是,背包中每种物品的数量是无限的,可以多次选择,直到装不下位置。
有一种直接的考虑是将完全背包转换为\(01\)背包来处理,因为总容量是\(V\)固定的,每件物品的重量是\(w[i]\),可以将第i种物品转换为\(V/w[i]\)个\(i\)种物品,然后转换为\(01\)背包来处理。
同样可以根据\(01\)背包的思路,\(d[i] [j]\)表示从前\(i\)件物品中选择重量不超过\(j\)的物品的价值最大值。每种物品也是有放和不放两种思路,不过放的情况需要考虑放多少个物品i进去。
很容易想到状态转移方程为:
\(d[i] [j] = max ( d[i-1] [j], d[i-1] [j - k*w[i]] + k * v[i] | 0 <= k*w[i] <= j)\)
和\(01\)背包一样有\(O(NV)\)个状态需要求解,不过每个状态的求解不是常数,求解\(d[i] [j]\)的时间为\(O(j/w[i])\)。
参考程序
#include <iostream>
#include <algorithm>
#define N 35
#define M 205
using namespace std;
int main () {
int m, n, w[N], c[N], d[N][M] = {0};
cin >> m >> n;
for (int i = 1; i <= n; i++)
cin >> w[i] >> c[i];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (j >= w[i]) {
int k = j / w[i];
for (; k >= 0; k--)
d[i][j] = max (d[i][j], d[i-1][j - k*w[i]] + c[i]*k);
} else
d[i][j] = d[i-1][j];
}
}
cout << "max=" <<d[n][m];
return 0;
}
问题优化
考虑\(01\)背包的问题优化,\(01\)背包逆推的原因在于第\(i\)次循环中的状态必须由\(i-1\)的状态得来,而完全背包的特点是每种物品可以选择无限的个数,因此在考虑选择第\(i\)件物品的时候,需要一个可能已经入选了第\(i\)种物品的子结果,因此可以采取顺推的方式进行。
参考程序
#include <iostream>
#include <algorithm>
#define N 35
#define M 205
using namespace std;
int main () {
int m, n, w[N], c[N], d[M] = {0};
cin >> m >> n;
for (int i = 1; i <= n; i++)
cin >> w[i] >> c[i];
for (int i = 1; i <= n; i++) {
for (int j = w[i]; j <= m; j++)
d[j] = max (d[j], d[j-w[i]]+c[i]);
}
cout << "max=" << d[m];
return 0;
}
【问题描述】
设有\(n\)种物品和一个最大载重量为\(M\)的背包,每种第i种物品最多有\(n[i]\)件,每件重量是\(w[i]\)。价值是\(c[i]\)。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
【输入】
第一行二个数\(n(n ≤ 500),m(m ≤ 6000)\),其中\(n\)表示物品数量,\(m\)表示背包容量。
接下来\(n\)行,每行\(3\)个数,\(w、c、s\),分别表示第\(i\)种物品的重量、价值(价格与价值是不同的概念)和该种物品的最大数量(买\(0\)件到\(s\)件均可),其中\(v ≤ 100,w ≤ 1000,s ≤ 10\)。
【输出】
输出一行表示最大价值
【样例输入】
5 1000
80 20 4
40 50 9
30 50 7
40 30 6
20 20 1
【样例输出】
1040
多重背包和完全背包思路类似,只是从无限获取变成了有限制的获取,稍微改一下状态转移方程即可:
\(d[i] [j] = max ( d[i-1] [j], d[i-1] [j - k*w[i]] + k * v[i] | 0 <= k*w[i] <= j \,\, and \,\, k <= n[i])\)
参考程序
#include <iostream>
#include <algorithm>
#define N 505
#define M 6005
using namespace std;
int m, n, w[N], c[N], num[N], d[N][M];
int main () {
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> w[i] >> c[i] >> num[i];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (j >= w[i]) {
int t = j / w[i];
for (int k = 0; k <= t && k <= num[i]; k++)
d[i][j] = max (d[i][j], d[i-1][j - k*w[i]] + c[i]*k);
}else
d[i][j] = d[i-1][j];
}
}
cout << d[n][m];
return 0;
}
进一步优化:
多重背包也可以转换为\(01\)背包求解,将第i类物品转换为\(n[i]\)件\(01\)背包中的物品,那么就变成了总物品数量为\(\sum n[i]\)的\(01\)背包。
转化为\(01\)背包后,要是有方法能够降低复杂度就好了,实际上可以通过二进制来进行优化。将第\(i\)种物品分为若干件物品,其中每一个物品有一个系数,表示该物品的费用和价值是这个系数乘以原物品的费用和价值。这些系数可以用\(2\)的幂来表示,也就是\(1、2、4、8.....2^{(k-1)}、n[i]-2^k+1\)。这个序列中\(k\)是满足\(n[i]-2^{(k)}+1>0\)的最大整数。
将这若干件有系数的物品组合起来,能表示出\(0~n[i]\)范围内的任意一个数字,这一点很重要,是能够进行二进制优化的关键所在。例如\(n[i]=13\)时,原本是\(13\)件物品,可以通过二进制优化成系数为\(1、2、4、6\)的\(4\)件物品。并且\(1、2、4、6\)的组合能够表示出\(0~13\)中间任意的数字。
合理性证明
可以将系数分成两段来简单证明,第一段是\(0\)到\(2^k-1\).第二段是\(2^k\)到\(n[i]\)。拿\(13\)来举例分成第一段\(0\)到\(7\)和第二段\(8\)到\(13\),对于第一段来说,\(7\)的二进制为\(111\),对于这三个位置的\(1\)可以通过取或者不取,这样就可以表示出\(0\)到\(7\)之间的所有数字。而第二段则可以整体减去\(6\),变成\(2\)到\(7\),这样就可以通过第一段的数字加上\(6\)来表示\(8\)到\(13\)区间内的所有数字
因此,\(0\)到\(13\)之间的任意数字都可以被\(1、2、4、6\)的组合表示出来。时间复杂度就会降低为\(O(V*\)\(\sum log(n[i])\))。
参考程序(二进制优化)
#include <iostream>
#include <algorithm>
#define N 20005
using namespace std;
int w[N], c[N], num[N];
long long d[N];
inline void read (int &x) {
char c; x = 0; bool f = 0;
c = getchar();
while (c > ‘9‘ || c < ‘0‘) {if(c == ‘-‘) f = 1; c = getchar();}
while (c >= ‘0‘ and c <= ‘9‘) {x = (x << 3) + (x << 1) + c - 48; c = getchar();}
if (f == 1) x = -x;
}
int main () {
int n, v, cnt = 1, x, y, z;
read(n), read(v);
for (int i = 1; i <= n; i++) {
read(x), read(y), read(z);
int t = 1;
while (t <= z) { // 转换为二进制
w[cnt] = t * x;
c[cnt] = t * y;
cnt ++;
z -= t;
t *= 2;
}
if (z > 0) {
w[cnt] = z * x;
c[cnt] = z * y;
cnt ++;
}
}
for (int i = 1; i <= cnt; i++)
for (int j = v; j >= w[i]; j--)
d[j] = max (d[j], d[j-w[i]] + c[i]);
cout << d[v];
return 0;
}
单调队列优化:
实际上多重背包的复杂度还可以进一步降低,可以考虑使用单调队列
首先来看朴素的多重背包
\(f[j] = max (f[j], f[j - k * v] + k * w) | k <= s \,\,and\,\, k * v <= j\)
如果能将求\(f[j]\)的过程在\(O(1)\)的时间内算出来,那么整体复杂度为\(O(NV)\)
如果将所有的体积进行分类,\(j \% v\)的结果进行分类,所有结果为\(j \% v == 0\)的分为一类,所有结果为\(j \% v == 1\)的分为一类,每一类完全没有交集。可以将整体体积\(m\)分为\(v\)类。
观察上述朴素的多重背包状态转移方程,\(f[j]\)只会从\(f[j - k * v]\)中转移过来,按照分类,只会从同一类转移过来。
因此我们分别去考虑每一类,考虑的过程中,假定在算\(f[j]\)的时候,需要知道一共要用多少个第\(i\)个物品,因此有
\(f[j] = max (f[j], f[j - v] + w, f[j - 2 * v] + 2 * w, f[j - k * v] + k * w)\)
接下来按照分类,将f[0] 到 f[m] 总体积的过程写成如下表达
\(f[0] , f[v], f[2 * v], f[3 * v], ......, f[k * v]\)
\(f[1], f[v + 1], f[2 * v + 1], f[3 * v + 1], ......, f[k * v + 1]\)
\(f[2], f[v + 2], f[2 * v + 2], f[3 * v + 2], ......, f[k * v + 2]\)
......
\(f[j], f[v + j], f[2 * v + j], f[3 * v + j], ......, f[k * v + j]\)
将全部的体积分为上面的v个类别,其中\(m = k * v + j, 0 <= j < v\)。每一类中的值都是转换的
\(f[k * v + j]\)只依赖于 {\(f[j], f[v + j], f[2 * v + j],......, f[k * v + j]\)}中的最大值,因此可以通过单调队列来维护这个序列中的最大值,这样能在\(O(1)\)的时间找出最大值。
因此,我们可以得到
\(f[j] = f[j]\)
\(f[j + v] = max(f[j] + w, f[j + v])\)
\(f[j + 2 * v] = max(f[j] + 2 * w, f[j + v] + w, f[j + 2 * v])\)
\(f[j + 3 * v] = max(f[j] + 3 * w, f[j + v] + 2 * w, f[j + 2 * v] + w, f[j + 3 * v])\)
......
但是,这个队列中前面的数,每次都会增加一个 w ,所以我们需要做一些转换,方便单调队列的运算
\(f[j] = f[j]\)
\(f[j + v] = max(f[j], f[j + v] - w) + w\)
\(f[j + 2 * v] = max(f[j], f[j + v] - w, f[j + 2 * v] - 2 * w) + 2 * w\)
\(f[j + 3 * v] = max(f[j], f[j + v] - w, f[j + 2 * v] - 2 * w, f[j + 3 * v] - 3 * w) + 3 * w\)
......
这样,每次入队的值是\(f[j + k * v] - k * w\)
单调队列问题,最重要的两点
1)维护队列元素的个数,如果不能继续入队,弹出队头元素
2)维护队列的单调性,即:尾值\(>= f[j + k * v] - k * w\)
参考程序
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 2e4 + 10;
int m, n;
int f[N], g[N], q[N];
int main () {
int v, w, s;
cin >> n >> m;
for (int i = 1; i <= n; i ++) {
cin >> v >> w >> s;
memcpy (g, f, sizeof f);
// g[] 表示f[i-1]
for (int j = 0; j < v; j ++) {
/**
体积为c 分为c类,枚举一下所有的余数
每一类相互独立的
**/
int hh = 0, tt = -1;
// hh 表示队首位置,tt表示队尾位置
for (int k = j; k <= m; k += v) {
/**
枚举同一类中的背包体积
**/
// f[k] = g[k];
if (hh <= tt and k - s * v > q[hh]) hh ++;
/*
如果区间不合法则取出队首
该区间维护的是不超过s长度的区间
k - s * v > q[hh] (表示当前编号减去队列最大容积大于队首,队首出队)
*/
if (hh <= tt) f[k] = max (f[k], g[q[hh]] + (k - q[hh]) / v * w);
/**
用最大数更新当前的数
(k - q[hh]) / v * w 相当于k * w,
(k- q[hh])为位置长度,除以体积c表示可以放c体积的数量
**/
while (hh <= tt and g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) tt --;
/**
插入当前数字,并保证单调性
保证队尾的值刚好大于当前的值
凡是比队尾(g[q[tt]]-(q[tt] - j) / v*w)的值比当前值小(g[k]-(k - j) / v*w)的都舍去
**/
q[ ++ tt ] = k; // 当前位置信息加入进队列
}
}
}
cout << f[m];
return 0;
}
【问题描述】
有\(N\) 种物品和一个容量是 \(V\)的背包。
物品一共有三类:
每种体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
【输入格式】
第一行两个整数\(N,V\),用空格隔开,分别表示物品种数和背包容积。
接下来有 \(N\)行,每行三个整数\(v_i,w_i,s_i\),用空格隔开,分别表示第\(i\)种物品的体积、价值和数量。
【输出格式】
输出一个整数,表示最大价值。
【数据范围】
\(0<N,V≤1000\)
\(0<v_i,w_i≤1000\)
\(?1≤s_i≤1000\)
【输入样例】
4 5
1 2 -1
2 4 1
3 4 0
4 5 2
【输出样例】
8
实际上混合背包就是将前\(3\)种背包放在了一起,这里就不说二维的方法了,考虑优化成一维的解法,实际上可以将多重背包用二进制优化成\(01\)背包,这样问题就转换成立\(01\)背包和完全背包的问题,那么在枚举背包容量的时候,只需要一个正序一个逆序即可。
参考程序
#include <iostream>
#include <algorithm>
#include <vector>
#define N 1005
using namespace std;
struct Pack {
int v, w, kind;
};
vector <Pack> p;
int f[N];
int main () {
int n, V;
int v, w, z;
cin >> n >> V;
for (int i = 1; i <= n; i++) {
cin >> v >> w >> z;
if (z == -1) p.push_back ({v, w, -1});
else if (z == 0) p.push_back ({v, w, 0});
else { // 转换为01背包
for (int k = 1; k <= z; k *= 2) {
p.push_back ({k*v, k*w, -1});
z -= k;
}
if (z > 0) p.push_back ({z*v, z*w, -1});
}
}
for (auto pack : p) {
if (pack.kind == -1)
for (int j = V; j >= pack.v; j--)
f[j] = max (f[j], f[j-pack.v] + pack.w);
else
for (int j = pack.v; j <= V; j++)
f[j] = max (f[j], f[j-pack.v] + pack.w);
}
cout << f[V];
return 0;
}
【问题描述】
有\(N\)件物品和一个容量是\(V\)的背包,背包能承受的最大重量是 \(M\)。
每件物品只能用一次。体积是 \(v_i\),重量是 \(m_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大。
输出最大价值。
【输入格式】
第一行三个整数,\(N,V,M\),用空格隔开,分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有\(N\)行,每行三个整数 \(v_i,m_i,w_i\),用空格隔开,分别表示第\(i\)件物品的体积、重量和价值。
【输出格式】
输出一个整数,表示最大价值。
【数据范围】
\(0<N≤1000\)
\(0<V,M≤100\)
\(0<v_i,m_i≤100\)
\(0<w_i≤1000\)
【输入样例】
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6
【输出样例】
8
对于一维的背包问题\(f[j]\)表示重量不超过\(j\)的物品的最大价值,那么二维的可以直接扩展一个维度
\(f[i][j]\)表示体积是\(i\)重量是\(j\)的情况下物品的最大价值
参考程序
#include <iostream>
#include <algorithm>
#define N 1005
using namespace std;
int v[N], m[N], w[N];
int f[N][N];
int main () {
int n, V, M;
cin >> n >> V >> M;
for (int i = 1; i <= n; i++)
cin >> v[i] >> m[i] >> w[i];
for (int i = 1; i <= n; i++)
for (int j = V; j >= v[i]; j--)
for (int k = M; k >= m[i]; k--)
f[j][k] = max (f[j][k], f[j-v[i]][k-m[i]] + w[i]);
cout << f[V][M];
return 0;
}
【问题描述】
有 \(N\) 组物品和一个容量是\(V\)的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 \(v_{ij}\),价值是\(w_{ij}\),其中 \(i\)是组号,\(j\)是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
【输入格式】
第一行有两个整数\(N,V\),用空格隔开,分别表示物品组数和背包容量。
接下来有\(N\)组数据:
【输出格式】
输出一个整数,表示最大价值。
【数据范围】
\(0<N,V≤100\)
\(0<S_i≤100\)
\(0<v_{ij},w_{ij}≤100\)
【输入样例】
3 5
2
1 2
2 4
1
3 4
1
4 5
【输出样例】
8
分组背包的特点就是将背包中的物品进行了分组,同一组中的互斥,只能选择一个。每组只能选一个物品或者不选。可以考虑如下的状态转移方程
假定\(d[i] [j]\) 表示从前i组中选择重量不超过j的最大价值,则有
\(d[i] [j] = max(d[i-1] [j], d[i-1] [j-v[i]] + w[i])\),当前这一组是由上一组转移过来的。简单想一下就能明白一维数组的优化:
\(d[j] = max (d[j], d[j-v[k]] + w[k])\) 其中\(k\)枚举当前第\(i\)个分组的所有物品,同时\(j\)需要逆序枚举。
参考程序
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 105;
int f[N], v[N], m[N];
int main () {
int n, V, s;
cin >> n >> V;
for (int i = 1; i <= n; i++) {
cin >> s;
for (int j = 1; j <= s; j++) {
cin >> v[j] >> m[j];
}
for (int j = V; j >= 0; j --) {
for (int k = 1; k <= s; k++) {
if (j >= v[k])
f[j] = max (f[j], f[j-v[k]]+m[k]);
}
}
}
cout << f[V];
return 0;
}
分组背包是很多变形的背包问题的基础,可以参考分组背包的模型。
【题目描述】
有\(N\) 个物品和一个容量是\(V\) 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示:
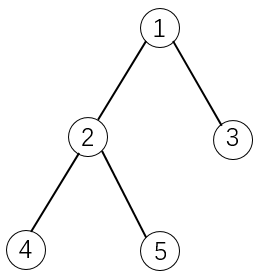
如果选择物品\(5\),则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。
每件物品的编号是\(i\),体积是 \(v_i\),价值是\(w_i\),依赖的父节点编号是 \(p_i\)。物品的下标范围是 \(1…N\)。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
【输入格式】
第一行有两个整数\(N,V\),用空格隔开,分别表示物品个数和背包容量。
接下来有\(N\) 行数据,每行数据表示一个物品。
第 \(i\) 行有三个整数 \(v_i,w_i,p_i\),用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果 \(p_i=?1\),表示根节点。 数据保证所有物品构成一棵树。
【输出格式】
输出一个整数,表示最大价值。
【数据范围】
\(1≤N,V≤100\)
\(1≤v_i,w_i≤100\)
父节点编号范围:
【输入样例】
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2
【输出样例】
11
这个问题由NOIP2006 中“金明的预算方案”一题扩展而来。遵从该题的提法,将不依赖于别的物品的物品称为“主件”,依赖于某主件的物品称为“附件”。由这个问题的简化条件可知所有的物品由若干主件和依赖于每个主件的一个附件集合组成。
按照背包问题的一般思路,仅考虑一个主件和它的附件集合。可是,可用的策略非常多,包括:一个也不选,仅选择主件,选择主件后再选择一个附件,选择主件后再选择两个附件……无法用状态转移方程来表示如此多的策略。事实上,设有n 个附件,则策略有2^n + 1 个,为指数级。
考虑到所有这些策略都是互斥的(也就是说,你只能选择一种策略),所以一个主件和它的附件集合实际上对分组背包中的一个物品组,每个选择了主件又选择了若干个附件的策略对应于这个物品组中的一个物品,其费用和价值都是这个策略中的物品的值的和。但仅仅是这一步转化并不能给出一个好的算法,因为物品组中的物品还是像原问题的策略一样多。
再考虑对每组内的物品优化。这提示我们,对于一个物品组中的物品,所有费用相同的物品只留一个价值最大的,不影响结果。所以,我们可以对主件i的“附件集合”先进行一次01背包,得到费用依次为0..V-c[i]所有这些值时相应的最大价值f‘[0..V-c[i]]。那么这个主件及它的附件集合相当于V-c[i]+1个物品的物品组,其中费用为c[i]+k的物品的价值为f‘[k]+w[i]。也就是说原来指数级的策略中有很多策略都是冗余的,通过一次01背包后,将主件i转化为 V-c[i]+1个物品的物品组,就可以直接应用P06的算法解决问题了。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m, root;
int h[N], e[N], ne[N], idx;
int v[N], w[N], f[N][N]; // f[i][j]表示选择节点i为根,所用的体积是j的情况下整棵子树的最大收益是多少。
/**
求一棵树的关系,可以从上往下用递归来做,每做到一个点的时候,先把所有子节点的f[i][j]算出来
每一个子节点都对应了在不同体积下的一个价值,因此可以当成分组背包,每一个子节点都是一个物品组
不同体积对应一个物品组,整个组只能选择一个物品
**/
void add (int a, int b) { // 有向图加入一条边,起点为a终点为b
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++;
}
void dfs (int u) {
for (int i = h[u]; i != -1; i = ne[i]) { // 循环物品组
int son = e[i]; // 递归求每一个物品时先将子节点算出来
dfs (son);
for (int j = m - v[u]; j >= 0; j --) {
/**
循环体积 (对比01背包 for (int j = V; j >= v[i]; j--))
必须选择物品u,u作为根节点(因此体积为m-v[u] 先空出来v[u]大小的空间)
**/
for (int k = 0; k <= j; k++)
/**
枚举分组(可选可不选) 当前子节点为根的子树看做一个组
不同的体积看做是组内的不同物品,算出该子节点用哪个体积收益最大
求出当前体积j下的最大收益f[u][j]
**/
f[u][j] = max (f[u][j], f[u][j - k] + f[son][k]);
}
}
for (int i = m; i >= v[u]; i --) f[u][i] = f[u][i - v[u]] + w[u]; // 如果体积大于v[u] 那么要填补空出来的位置,将根节点加入
for (int i = 0; i < v[u]; i ++) f[u][i] = 0; // 如果体积小于v[u]说明根节点不可选,那么子树也不可选,都赋值成0
}
int main () {
memset (h, -1, sizeof(h));
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int p;
cin >> v[i] >> w[i] >> p;
if (p == -1) root = i;
else add (p, i); // p表示父结点,i是当前第几个结点
}
dfs (root);
cout << f[root][m] << endl;
return 0;
}
【问题描述】
有\(N\)件物品和一个容量是 \(V\)的背包。每件物品只能使用一次。
第\(i\)件物品的体积是 \(v_i\),价值是\(w_i\)。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 最优选法的方案数。注意答案可能很大,请输出答案模\(10^9+7\)的结果。
【输入格式】
第一行两个整数,\(N,V\),用空格隔开,分别表示物品数量和背包容积。
接下来有\(N\) 行,每行两个整数\(v_i,w_i\),用空格隔开,分别表示第\(i\)件物品的体积和价值。
【输出格式】
输出一个整数,表示 方案数 模\(10^9+7\)的结果。
【数据范围】
\(0<N,V≤1000\)
\(0<v_i,w_i≤1000\)
【输入样例】
4 5
1 2
2 4
3 4
4 6
【输出样例】
2
问题分析
按照\(01\)背包一维表示方法,\(f[j]\)表示重量不超过j的情况下的最大价值。
状态转移为\(f[j] = max (f[j], f[j-w[i]] + c[i])\)
定义 \(cnt[j]\)表示重量不超过\(j\)的情况下,所产生的最大价值的最大方案数。
显然,\(cnt\)应该初始化为\(1\),什么都不选也是一种方案。
如果选择了当前的第\(i\)个物品,那么\(cnt[j] = cnt[j-w[i]]\),方案数和转移过来的那个状态的方案数相同。
还有一种情况则是当\(f[j] == f[j-w[i]]+c[i]\)时,此时的\(f\)不需要转移,选择或者不选第\(i\)个物品当前容量下的最大价值都没有变化,但是由此产生的方案数发生了变化。因此\(cnt[j] = cnt[j] + cnt[j-w];\)
参考程序
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1005;
const int mod = 1e9 + 7;
int f[N], cnt[N];
int main () {
int n, v, c, w;
cin >> n >> v;
for (int i = 0; i <= v; i++) cnt[i] = 1;
for (int i = 1; i <= n; i++) {
cin >> w >> c;
for (int j = v; j >= w; j--) {
if (f[j] < f[j-w]+c) {
f[j] = f[j-w] + c;
cnt[j] = cnt[j-w];
} else if (f[j] == f[j-w] + c)
cnt[j] = (cnt[j] + cnt[j-w]) % mod;
}
}
cout << cnt[v] << endl;
return 0;
}
【问题描述】
有\(N\)件物品和一个容量是\(V\) 的背包。每件物品只能使用一次。
第\(i\) 件物品的体积是\(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 字典序最小的方案。这里的字典序是指:所选物品的编号所构成的序列。物品的编号范围是\(1…N\)。
【输入格式】
第一行两个整数\(N,V\),用空格隔开,分别表示物品数量和背包容积。
接下来有\(N\) 行,每行两个整数\(v_i,w_i,\)用空格隔开,分别表示第\(i\)件物品的体积和价值。
【输出格式】
输出一行,包含若干个用空格隔开的整数,表示最优解中所选物品的编号序列,且该编号序列的字典序最小。
物品编号范围是 \(1…N。\)
【数据范围】
\(0<N,V≤1000\)
\(0<v_i,w_i≤1000\)
【输入样例】
4 5
1 2
2 4
3 4
4 6
【输出样例】
1 4
由于是要考虑字典序最小,可以重新考虑如下状态转移方程
\(f[i][j]\)表示从第\(i\)个物品到第\(n\)个物品中选择重量不超过\(j\)的最大价值。
那么稍加思考可以得出状态转移方程如下:(逆推)
\(f[i][j] = max (f[i+1] [j], f[i+1] [j - w] + c); i\)从\(n\)到\(1\)枚举
这样做的目的是为了方便我们进行查找。
如果存在一个选了物品1的的最优方案,那么答案中一定包含\(1\),原本容量\(v\),现在变成容量为\(v-w[1]\)的背包,物品为\(2...N\)的子问题。同样如果物品不包含物品\(1\),那么同样变成容量为\(v-w[1]\)的背包,物品为\(2...N\)的子问题。
具体操作表现为(顺推)
如果\(f[i] [v] == f[i+1] [v-w[i]] + c[i]\),那么一定要选择物品i,说明选了物品能够得到最大价值(根据\(f[i] [j]\)的状态定义来看)
如果\(f[i] [v] == f[i+1] [j]\),说明不选i也能得到最优解。
如果\(f[i] [v] == f[i+1] [j] == f[i+1] [v-w[i]] + c[i]\),那么根据字典序最小原则,应该按照选择物品\(i\)来输出方案
参考程序
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1005;
int w[N], c[N], f[N][N];
int main () {
int n, v;
cin >> n >> v;
for (int i = 1; i <= n; i++) {
cin >> w[i] >> c[i];
}
for (int i = n ; i >= 1; i --) {
for (int j = 0; j <= v; j++) {
if (j >= w[i])
f[i][j] = max (f[i+1][j], f[i+1][j-w[i]]+c[i]);
else f[i][j] = f[i+1][j];
}
}
int stor = v;
for (int i = 1; i <= n; i++) {
if (stor <= 0) break;
if (stor >= w[i] && f[i][stor] == f[i+1][stor-w[i]]+c[i]) { //选择i可以得到最优解,输出
cout << i << " ";
stor -= w[i];
}
}
return 0;
}
背包问题的枚举解决方式一般都是
1、枚举循环物品
2、枚举循环体积
3、枚举循环策略
状态的定义需要灵活使用,不同的状态需要进行不同的初始化,例如对于01背包来讲。有的题目要求“恰好装满背包”时的最优解,有的题目则并没有要求必须把背包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。
如果是第一种问法,要求恰好装满背包,那么在初始化时除了\(f[0]\)为0,其它\(f[1 : v]\)均设为\(-inf\),这样就可以保证最终得到的\(f[V]\) 是一种恰好装满背包的最优解。
如果并没有要求必须把背包装满,而是只希望价格尽量大,初始化时应该将\(f[0 : v]\)全部设为0。
初始化的f数组事实上就是在没有任何物品可以放入背包时的合法状态。如果要求背包恰好装满,那么此时只有容量为0的背包可以在价值为0的情况下被“恰好装满”,其它容量的背包均没有合法的解,属于未定义的状态,应该被赋值为\(-inf\)了。(f[v]是通过max函数来选择,-inf是不会被选中的)
如果背包并非必须被装满,那么任何容量的背包都有一个合法解“什么都不装”,这个解的价值为0,所以初始时状态的值也就全部为0了。
原文:https://www.cnblogs.com/s-k-p/p/13768402.html