同余
如果\(a\div n\)和\(b\div n\)余数相同,则说a和b同余,记作\(a\equiv b(\mod n)\)。
如
\[8\equiv 1(\mod 7)\6\equiv 2(\mod 4)
\]
同余类
任意一个数m除n的余数在0~n-1之间。这0~n个数就代表一个数余n的同余类。
如7的同余类有\([0],[1],[2],[3],[4],[5],[6]\)。任何一个数除7得到的余数必在这些同余类中。
看一下日历
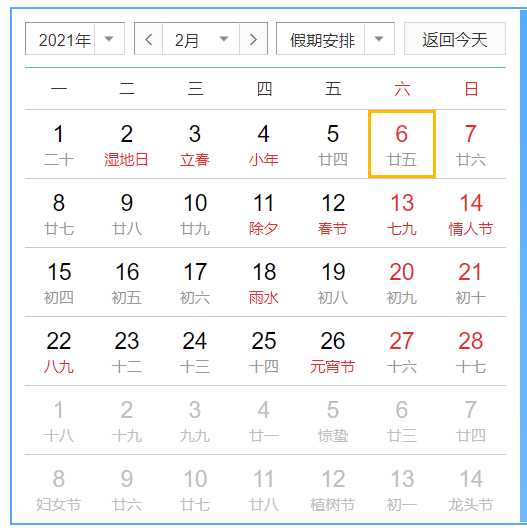
每一列中的数余7得到的余数都相等,第一列余7都是1,则这几个数在\([1]\)这个同余类中,第二列则在\([2]\)的同余类中。依此类推。
同余类性质
除了上面两个基本的性质外,同余还有一个最重要的性质,它直接引出了后面的费马小定理和欧拉定理。
同余性质
\[如果a\equiv c(\mod n),\ b\equiv d(\mod n)\那么a\plusmn b=c\plusmn d(\mod n)\ab=cd(\mod n)\ka\equiv kb(\mod n)\a^m\equiv b^m(\mod n)\\]
还有一个性质,如果c和m互素,则c可以从同余式中消去,如下
\[ac=bc(\mod m)\如果(c,m)=1\a=b(\mod m)
\]
费马小定理
费马小定理是说,如果\((a,m)=1\),\(m\)是素数,则
\[a^{m-1}\equiv 1(\mod n)
\]
证明下
\[m不是1,2,3,...,m-1的素因数\\because (a,m)=1\therefore m不是a的素因数\\therefore m不是a,2a,3a,...,a(m-1)的素因数\\therefore a^{m-1}(m-1)!=(m-1)!(\mod m)\\because ((m-1)!,m)=1\\therefore a^{m-1}=1(\mod m)
\]
欧拉定理
欧拉定理是说,如果\((a,m)=1\),\(\varphi (m)\)代表1~m之间和m互素的正整数个数,则
\[a^{\varphi (m)}=1(\mod m)
\]
证明
\[\because设a_1,a_2,...,a_r为1到m之间和m互素的正整数,(a,m)=1\\therefore a_1a\ a_2a\ ... a_3a=a_1a_2...a_r(\mod m)\a^r=(\mod m)
\]
例子
\(求13^{2004}除以17的余数\)
\[\because (7,13)=1,\ 且17是素数\\therefore 13^{16}\equiv 1(\mod 17)\13^{2004}=(13^{16})^{125}+13^4\equiv 13^4(\mod 17)\13^4=169^2=(170-1)^2=(-1)^2(\mod 17)\\therefore 13^{2004}\equiv 1(\mod 17)
\]
数论——同余
原文:https://www.cnblogs.com/lilpig/p/13773093.html
