1，按位运算:符号|按位OR运算；符号&按位AND运算；符号~表示按位NOT运算；符号^按位XOR运算。
实现掩码操作：通过与给定的一个位模式进行按位与，可以提取所需要的位，对这些位进行“置1” “清0”等。
2，符号||按位OR运算；符号&&表示AND运算；符号！表示NOT运算。
3，移位运算辑移位和算术移位。
逻辑移位：不考虑符号位，把高（低）位移出，低（高）补0.
原码的移位：原码算术移位:左移丢1,运算会出错,右移丢1,会影响精度
补码的移位：正数中，原码，补码，反码左右移都补0，负数中，原码左右移补0，补码左移补0、右移补1，反码左右移补1。
4，位扩展和位截断运算
两种位扩展方式：0扩展和符号扩展。0扩展用于无符号数，符号扩展用于补码表示的带符号整数

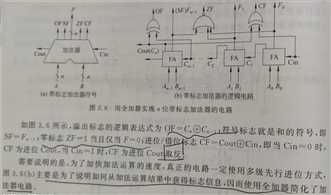
用n位全加器实现两个n位操作数各位同时相加，这种加法器称为并行加法器。并行加法器中全加器的个数与操作数的位数相同。
并行加法器中全加器的位数与操作数的位数相同，可同时对操作数的各位相加。
计算机内部大多采用两级或多级先行进位加法器。

比较两个操作数的符号，对加法实行“同号求和，异号求差”，对减法实行“异号求和，同号求差
求和时，数值位相加，若最高位产生进位则结果溢出
求差时，被加数数值位加上加数数值位的补码

补码恢复余数除法
采用“够减则上商为1，不够减则上商为0”的上商方式，因此，最后若商为负值，则需要“各位取反，末位加1”来得到真正的商

补码不恢复余数除法
被除数与除数同号，被除数减去除数；被除数与除数异号，被除数加上除数。余数与除数同号，商上1，余数左移一位减去除数；
余数与除数异号，商上0，余数左移一位加上除数。（注意：余数左移加上或减去除数后就得到了新余数。直到商的位数满足要求为止。

先进行判0处理，规格化操作和溢出判断

（1）乘法运算：尾数相乘，指数相加；尾数规格化；尾数舍入处理；溢出判断浮点数除法运算

（2）除法运算：尾数相除，阶相减；尾数规格化；尾数舍入处理；溢出判断