实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。
示例:
Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // 返回 true trie.search("app"); // 返回 false trie.startsWith("app"); // 返回 true trie.insert("app"); trie.search("app"); // 返回 true
说明:
你可以假设所有的输入都是由小写字母 a-z 构成的。
保证所有输入均为非空字符串。
正常的树节点定义是怎么样的
struct TreeNode { VALUETYPE value; //结点值 TreeNode* children[NUM]; //指向孩子结点 };
下面是Trie的结点定义,体会二者的不同
1 class Trie { 2 3 boolean isEnd = false; // 标记是否为最终结点 4 Trie[] next; // 所有孩子结点 5 6 /** Initialize your data structure here. */ 7 public Trie() { 8 next = new Trie[26]; // 26个孩子结点 9 } 10 }
描述:向 Trie 中插入一个单词 word
实现:这个操作和构建链表很像。首先从根结点的子结点开始与 word 第一个字符进行匹配,一直匹配到前缀链上没有对应的字符,这时开始不断开辟新的结点,直到插入完 word 的最后一个字符,同时还要将最后一个结点isEnd = true;,表示它是一个单词的末尾。
1 public void insert(String word) { 2 // 有则共享且继续向下遍历,否则新建结点 3 Trie node = this; // node指针用来遍历 4 for(char ch : word.toCharArray()){ 5 int index = ch - ‘a‘; 6 if(node.next[index] == null){ // 新建结点 7 node.next[index] = new Trie(); 8 } 9 node = node.next[index]; // 指针后移 10 } 11 node.isEnd = true; // 标记为最终结点 12 }
描述:查找 Trie 中是否存在单词 word
实现:从根结点的子结点开始,一直向下匹配即可,如果出现结点值为空就返回 false,如果匹配到了最后一个字符,那我们只需判断 node->isEnd即可。
1 public boolean search(String word) { 2 // 一直向下遍历,如果某个结点没找到,直接返回false,结束查找后判断是否为最终结点 3 Trie node = this; 4 for(char ch : word.toCharArray()){ 5 int index = ch - ‘a‘; 6 if(node.next[index] == null){ 7 return false; 8 } 9 node = node.next[index]; // 指针后移 10 } 11 return node.isEnd; 12 }
描述:判断 Trie 中是或有以 prefix 为前缀的单词
实现:和 search 操作类似,只是不需要判断最后一个字符结点的isEnd,因为既然能匹配到最后一个字符,那后面一定有单词是以它为前缀的。
1 public boolean startsWith(String prefix) { 2 // 和search方法其实差不多,但是结束判断后直接返回true, 因为是判断前缀而已 3 Trie node = this; 4 for(char ch : prefix.toCharArray()){ 5 int index = ch - ‘a‘; 6 if(node.next[index] == null){ 7 return false; 8 } 9 node = node.next[index]; // 指针后移 10 } 11 return true; 12 }
1 class Trie { 2 3 boolean isEnd = false; // 标记是否为最终结点 4 Trie[] next; // 所有孩子结点 5 6 /** Initialize your data structure here. */ 7 public Trie() { 8 next = new Trie[26]; // 26个孩子结点 9 } 10 11 /** Inserts a word into the trie. */ 12 public void insert(String word) { 13 // 有则共享且继续向下遍历,否则新建结点 14 Trie node = this; // node指针用来遍历 15 for(char ch : word.toCharArray()){ 16 int index = ch - ‘a‘; 17 if(node.next[index] == null){ // 新建结点 18 node.next[index] = new Trie(); 19 } 20 node = node.next[index]; // 指针后移 21 } 22 node.isEnd = true; // 标记为最终结点 23 } 24 25 /** Returns if the word is in the trie. */ 26 public boolean search(String word) { 27 // 一直向下遍历,如果某个结点没找到,直接返回false,结束查找后判断是否为最终结点 28 Trie node = this; 29 for(char ch : word.toCharArray()){ 30 int index = ch - ‘a‘; 31 if(node.next[index] == null){ 32 return false; 33 } 34 node = node.next[index]; // 指针后移 35 } 36 return node.isEnd; 37 } 38 39 /** Returns if there is any word in the trie that starts with the given prefix. */ 40 public boolean startsWith(String prefix) { 41 // 和search方法其实差不多,但是结束判断后直接返回true, 因为是判断前缀而已 42 Trie node = this; 43 for(char ch : prefix.toCharArray()){ 44 int index = ch - ‘a‘; 45 if(node.next[index] == null){ 46 return false; 47 } 48 node = node.next[index]; // 指针后移 49 } 50 return true; 51 } 52 }
leetcode执行用时:41 ms > 85.59%, 内存消耗:49.4 MB > 33.00%
时间复杂度:插入、查询、前缀匹配都是O(n), n为为字符串长度
空间复杂度: 每个结点都需要一个26大小的数组,Trie 的每个结点中都保留着一个字母表,这是很耗费空间的。如果 Trie 的高度为 n,字母表的大小为 m,最坏的情况是 Trie 中还不存在前缀相同的单词,那空间复杂度就为 O(m^n)。
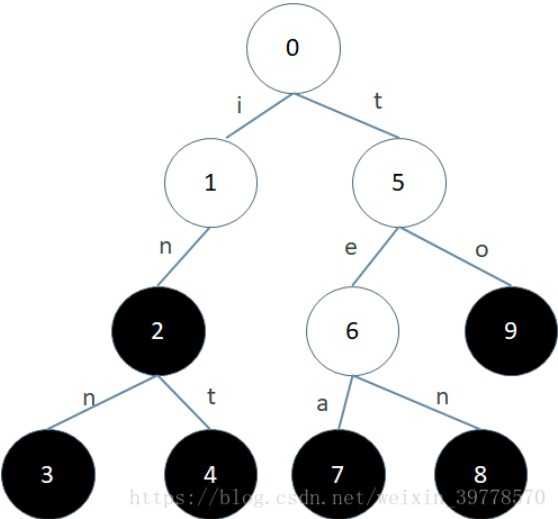
数据规模为n时,二叉搜索树插入、查找、删除操作的时间复杂度通常只有O(logn),最坏情况下整棵树所有的节点都只有一个子节点,退变成一个线性表,此时插入、查找、删除操作的时间复杂度是O(n)。
? ?通常情况下,Trie树的高度n要远大于搜索字符串的长度m,故查找操作的时间复杂度通常为O(m),最坏情况下的时间复杂度才为O(n)。很容易看出,Trie树最坏情况下的查找也快过二叉搜索树。
原文:https://www.cnblogs.com/hi3254014978/p/13777810.html