【深度学习实战】Pytorch Geometric实践——利用Pytorch搭建GNN-布布扣-bubuko.com

1. 安装

首先，我们先查一下我们的pytorch的版本。要求至少安装 PyTorch 1.2.0 版本：

python -c "import torch; print(torch.__version__)"

接着，查询对应pytorch安装的CUDA的版本：

python -c "import torch; print(torch.version.cuda)"

然后，安装Pytorch geometry的软件包。需要注意的是，这里的${CUDA}是前面查询到的CUDA的版本(cpu, cu92, cu101, cu102)，${TORCH}是前面查到的pytorch的版本。（建议将pytorch升级到最新版本再进行安装）

pip install torch-scatter==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-${TORCH}.html
pip install torch-sparse==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-${TORCH}.html
pip install torch-cluster==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-${TORCH}.html
pip install torch-spline-conv==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-${TORCH}.html
pip install torch-geometric

比如我这里查到Pytorch的版本是1.5.1（按照官网的教程，pytorch版本为1.5.0或者1.5.1的按照1.5.0来安装），CUDA的版本是10.2，那么我的安装语句如下：

pip install torch-scatter==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.5.0.html
pip install torch-sparse==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.5.0.html
pip install torch-cluster==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.5.0.html
pip install torch-spline-conv==latest+cu102 -f https://pytorch-geometric.com/whl/torch-1.5.0.html
pip install torch-geometric

2. 基本概念介绍

2.1 Data Handling of Graphs 图形数据处理

图（Graph）是描述实体（节点）和关系（边）的数据模型。在Pytorch Geometric中，图被看作是torch_geometric.data.Data的实例，并拥有以下属性：

属性	描述
`data.x`	节点特征，维度是`[num_nodes, num_node_features]`。
`data.edge_index`	维度是`[2, num_edges]`，描述图中节点的关联关系，每一列对应的两个元素，分别是边的起点和重点。数据类型是`torch.long`。需要注意的是，`data.edge_index`是定义边的节点的张量（tensor），而不是节点的列表（list）。
`data.edge_attr`	边的特征矩阵，维度是`[num_edges, num_edge_features]`
`data.y`	训练目标（维度可以是任意的）。对于节点相关的任务，维度为`[num_nodes, ]`；对于图相关的任务，维度为`[1,]`。
`data.position`	节点位置矩阵（Node position matrix），维度为`[num_nodes, num_dimensions]`。

下面是一个简单的例子：

首先导入需要的包：

import torch
from torch_geometric.data import Data

比如上图所示的图结构，我们首先定义节点特征向量：

x = torch.tensor([[-1], [0], [1]], dtype=torch.float)

接着定义边，下面两种定义方式是等价的。第二种方式可能更符合我们的阅读习惯，但是需要注意的是此时应当增加一个edge_index=edge_index.t().contiguous()的操作。此外，由于是无向图，虽然只有两条边，但是我们需要四组关系说明来描述边的两个方向。

## 法1
edge_index = torch.tensor([[0, 1, 1, 2],
                           [1, 0, 2, 1]], dtype=torch.long)
data = Data(x=x, edge_index=edge_index)

## 法2
edge_index = torch.tensor([[0, 1],
                           [1, 0],
                           [1, 2],
                           [2, 1]], dtype=torch.long)
data = Data(x=x, edge_index=edge_index.t().contiguous())

可以得到：

同时，Data对象提供了一些很实用的函数：

print(‘data\‘s keys: {}‘.format(data.keys))
print(‘-‘*5)
for key, item in data:
    print("{} found in data".format(key))
print(‘-‘*5)  
print(‘Does data has attribute \‘edge_attr\‘? {}‘.format(‘edge_attr‘ in data))
print(‘data has {} nodes‘.format(data.num_nodes))
print(‘data has {} edges‘.format(data.num_edges))
print(‘The nodes in data have {} feature(s)‘.format(data.num_node_features))
print(‘Does data contains isolated nodes? {}‘.format(data.contains_isolated_nodes()))
print(‘Does data contains self loops? {}‘.format(data.contains_self_loops()))
print(‘is data directed? {}‘.format(data.is_directed()))
print(data[‘x‘])

输出：

data‘s keys: [‘x‘, ‘edge_index‘]
-----
edge_index found in data
x found in data
-----
Does data has attribute ‘edge_attr‘? False
data has 3 nodes
data has 4 edges
The nodes in data have 1 feature(s)
Does data contains isolated nodes? False
Does data contains self loops? False
is data directed? False
tensor([[-1.],
        [ 0.],
        [ 1.]])

同样可以在GPU上运行data：

device = torch.device(‘cuda‘)
data = data.to(device)

2.2 Common Benchmark Datasets 常见的基准数据集

PyTorch Geometric提供很多基准数据集，包括

all Planetoid datasets (Cora, Citeseer, Pubmed)
all graph classification datasets from http://graphkernels.cs.tu-dortmund.de and their cleaned versions
the QM7 and QM9 dataset
a handful of 3D mesh/point cloud datasets like FAUST, ModelNet10/40 and ShapeNet

想要使用这些数据集，只要进行初始化，数据就会自动下载。比如我们要使用ENZYMES数据集(该数据集包括600张图，有6个类别)：

from torch_geometric.datasets import TUDataset
dataset = TUDataset(root=‘.\data\ENZYMES‘, name=‘ENZYMES‘)

程序就会自动执行下载：

Downloading http://ls11-www.cs.tu-dortmund.de/people/morris/graphkerneldatasets/ENZYMES.zip
Extracting data\ENZYMES\ENZYMES\ENZYMES.zip
Processing...
Done!

我们可以看一下这个数据集的一些属性：

print(dataset)
print(len(dataset))
print(dataset.num_classes)
print(dataset.num_node_features)

输出：

我们可以看下其中一张图的结构：

data = dataset[14]
print(data)
print(data.is_undirected())

输出：

我们可以看到数据集中的第一个图包含36个节点，每个节点有3个特征。图中有128/2 = 64条无向边，图被分类为“1”类。在将数据集分为训练集和测试集之前，可以调用dataset = dataset.shuffle()将数据集进行随机打乱。这个语句和下面这段程序是等价的：

perm = torch.randperm(len(dataset))
dataset = dataset[perm]

我们再来看硬外一个数据集Cora

from torch_geometric.datasets import Planetoid

dataset = Planetoid(root=‘.\data\Cora‘, name=‘Cora‘)
data = dataset[0]

print(data)
print(data.is_undirected())
print(data.train_mask.sum().item())
print(data.val_mask.sum().item())
print(data.test_mask.sum().item())

print(len(dataset))
print(dataset.num_classes)
print(dataset.num_node_features)

输出：

可以看到，前面的数据集针对的是“网络分类”的任务，而这个数据集针对的是“节点分类”的任务。每个节点又1433个特征，被分为7类。这个图是一个无向图，共有10556/2=5278条边，共有2708个节点。这里有三个需要注意的参数：

train_mask——指明训练集中的节点（可以看到，在这个数据集中，训练集里有140个节点）
val_mask——指明验证集中的节点（可以看到，在这个数据集中，验证集里有500个节点）
test_mask——指明测试集中的节点（可以看到，在这个数据集中，测试集里有1000个节点）

2.3 Mini-batches

神经网络通常以批处理的方式进行训练。在pytorch中，通常用数据加载器DataLoader来进行批处理。

from torch_geometric.datasets import TUDataset
from torch_geometric.data import DataLoader
from torch_scatter import scatter_mean

dataset = TUDataset(root=‘.\data\ENZYMES‘, name=‘ENZYMES‘, use_node_attr=True)
loader = DataLoader(dataset, batch_size=32, shuffle=True)

for data in loader:
    print(data)
    print(data.num_graphs)
    x = scatter_mean(data.x, data.batch, dim=0)
    print(x.size())

张图。

这个scatter函数实质上是对节点的一个整合，节点根据batch的标签（按照图）来进行整合，下面这张官方文档中的图可以很好地说明scatter函数的作用：

2.4 Data Transforms 数据转换

torch_geometric.transforms.Compose提供了数据转换的方法，可以方便用户将数据转换成既定的格式或者用于数据的预处理。在之前使用torchvision处理图像时，也会用到数据转换的相关方法，将图片转换成像素矩阵，这里的数据转换就类似torchvision在图像上的处理。

2.5 Learning Methods on Graphs——the first graph neural network 搭建我们的第一个图神经网络

下面我们来尝试着搭建我们的第一图神经网络。关于图神经网络，可以看一下这篇博客——GRAPH CONVOLUTIONAL NETWORKS。

数据集准备

我们使用的是Cora数据集。

from torch_geometric.datasets import Planetoid
dataset = Planetoid(root=‘./data/Cora‘, name=‘Cora‘)
print(dataset)

输出：

搭建网络模型

import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = GCNConv(dataset.num_node_features, 16)
        self.conv2 = GCNConv(16, dataset.num_classes)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index

        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)

        return F.log_softmax(x, dim=1)

模型的结构包含两个GCNConv层，选择ReLU作为非线性函数，最后通过softmax输出分类结果。

模型训练和验证

device = torch.device(‘cuda‘ if torch.cuda.is_available() else ‘cpu‘)
model = Net().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

model.train()
for epoch in range(200):
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()

model.eval()
_, pred = model(data).max(dim=1)
correct = int(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
acc = correct / int(data.test_mask.sum())
print(‘Accuracy: {:.4f}‘.format(acc))

输出：

3. CREATING MESSAGE PASSING NETWORKS 建立消息传递网络

将卷积神经网络中的“卷积算子”应用到图上面，核心在于neighborhood aggregation机制，或者说是message passing的机制。Aggregate Neighbours，核心思想在于基于局部网络连接来生成Node embeddings（Generate node embeddings based on local network neighborhoods）。如下面这个图：

例如图中节点A的embedding决定于其邻居节点

{ B , C , D } \{B,C,D\}

{B,C,D}，而这些节点又受到它们各自的邻居节点的影响。图中的“黑箱”可以看成是整合其邻居节点信息的操作，它有一个很重要的属性——其操作应该是顺序（order invariant）无关的，如求和、求平均、求最大值这样的操作，可以采用神经网络来获取。这样顺序无关的聚合函数符合网络节点无序性的特征，当我们对网络节点进行重新编号时，我们的模型照样可以使用。

那么，对于每个节点来说，它的计算图就由其邻居节点的数量来决定——

模型的深度可以自己定义（Model can be of arbitrary depth）：

Nodes have embeddings at each layer
Layer-0节点

3.1 Message passing 基本类

PyTorch Geometric 提供了基本类—— MessagePassing ，可以实现上述的图神经网络，来实现消息传递或消息聚集（which helps in creating such kinds of message passing graph neural networks by automatically taking care of message propagation. ）

MessagePassing类有三个参数：

aggr (string, optional) ——指定采用的置换不变函数，默认是add，可以定义为add、mean、max和None。
**flow (string, optional) **——指定信息传递的反向，默认是source_to_target，还可以设置为target_to_source。
**node_dim (int, optional) **——The axis along which to propagate. 默认是-2。

同时，MessagePassing提供了一些比较实用的方法：

MessagePassing.propagate(edge_index, size=None, **kwargs)

ii?全部设置为1。在pytorch geometric里面，是利用edge_index来实现。如果是有权图，则新增的自循环边以fill_value作为权。该方法最后返回两个值——`edge_index, edge_weight``。

import torch
from torch_geometric.utils import add_self_loops, degree

x = torch.tensor([[-1], [0], [1]], dtype=torch.float)
edge_index = torch.tensor([[0, 1, 1, 2],
                           [1, 0, 2, 1]], dtype=torch.long)

print("original edge_index ")
print(edge_index)

edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
print("new edge_index")
print(edge_index)

最后输出：

original edge_index 
tensor([[0, 1, 1, 2],
        [1, 0, 2, 1]])
new edge_index
tensor([[0, 1, 1, 2, 0, 1, 2],
        [1, 0, 2, 1, 0, 1, 2]])

Linearly transform node feature matrix. 第二步是对节点的特征矩阵进行线性变换。主要通过一个线性层torch.nn.Linear实现。
Compute normalization coefficients. 第三步是对变换后的节点特征进行标准化。节点的度可以通过torch_geometric.utils.degree实现。

import torch
from torch_geometric.utils import add_self_loops, degree

x = torch.tensor([[-1], [0], [1]], dtype=torch.float)
edge_index = torch.tensor([[0, 1, 1, 2],
                           [1, 0, 2, 1]], dtype=torch.long)

print("original edge_index ")
print(edge_index)

edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
print("new edge_index")
print(edge_index)

row, col = edge_index
deg = degree(col, x.size(0), dtype=x.dtype)
print(deg)
deg_inv_sqrt = deg.pow(-0.5)
print(deg_inv_sqrt)
print(deg_inv_sqrt[row])
print(deg_inv_sqrt[col])

最后输出：

original edge_index 
tensor([[0, 1, 1, 2],
        [1, 0, 2, 1]])
new edge_index
tensor([[0, 1, 1, 2, 0, 1, 2],
        [1, 0, 2, 1, 0, 1, 2]])
tensor([2., 3., 2.])
tensor([0.7071, 0.5774, 0.7071])
tensor([0.7071, 0.5774, 0.5774, 0.7071, 0.7071, 0.5774, 0.7071])
tensor([0.5774, 0.7071, 0.7071, 0.5774, 0.7071, 0.5774, 0.7071])

Sum up neighboring node features (“add” aggregation).

前面三步是message passing之前的预操作，第四、第五步可以采用MessagePassing类里面的方法完成。

完整的代码如下：

import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GCNConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super(GCNConv, self).__init__(aggr=‘add‘)  # "Add" aggregation (Step 5).
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def forward(self, x, edge_index):
        # x has shape [N, in_channels]
        # edge_index has shape [2, E]

        # Step 1: Add self-loops to the adjacency matrix.
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))

        # Step 2: Linearly transform node feature matrix.
        x = self.lin(x)

        # Step 3: Compute normalization.
        row, col = edge_index
        deg = degree(col, x.size(0), dtype=x.dtype)
        deg_inv_sqrt = deg.pow(-0.5)
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]

        # Step 4-5: Start propagating messages.
        return self.propagate(edge_index, x=x, norm=norm)

    def message(self, x_j, norm):
        # x_j has shape [E, out_channels]

        # Step 4: Normalize node features.
        return norm.view(-1, 1) * x_j

我们建立的这个神经网络模型GCNConv继承于基础类MessagePassing，并且采用求和函数作为

□ \square

□函数，通过super(GCNConv, self).__init__(aggr=‘add‘)来初始化。在完成1-3步之后，调用MessagePassing中的propagate()方法来完成4-5步，进行信息传播。message函数用于对节点的邻居节点的信息进行标准化。

我们可以通过一个案例来感受一下这个模型的输入和输出。

x = torch.tensor(torch.rand(3,2), dtype=torch.float)
edge_index = torch.tensor([[0, 1, 1, 2],
                           [1, 0, 2, 1]], dtype=torch.long)
conv = GCNConv(2, 4)

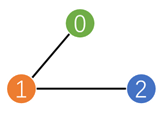
设有上图所示的网络，网络中有三个节点，每个节点有2个特征值。并构建神经网络conv = GCNConv(2, 4)。下面是程序运行的每一步输出的结果：

x is
tensor([[0.1819, 0.1848],
        [0.8479, 0.1754],
        [0.7511, 0.9781]])

----Step 1: Add self-loops to the adjacency matrix.----
tensor([[0, 1, 1, 2, 0, 1, 2],
        [1, 0, 2, 1, 0, 1, 2]])

----Step 2: Linearly transform node feature matrix.----
linear weight is 
Parameter containing:
tensor([[-0.6532, -0.3349],
        [ 0.5238, -0.5996],
        [-0.6279, -0.5872],
        [-0.4064,  0.5893]], requires_grad=True)
linear bias is
Parameter containing:
tensor([ 0.5966, -0.4339,  0.0263,  0.1577], requires_grad=True)
transformed x is
tensor([[ 0.4160, -0.4494, -0.1964,  0.1927],
        [-0.0159, -0.0949, -0.6090, -0.0835],
        [-0.2215, -0.6270, -1.0196,  0.4289]], grad_fn=<AddmmBackward>)

----Step 3: Compute normalization.----
tensor([0.4082, 0.4082, 0.4082, 0.4082, 0.5000, 0.3333, 0.5000])

----Step 4-5: Start propagating messages.----
tensor([[ 0.2015, -0.2635, -0.3468,  0.0623],
        [ 0.0741, -0.4711, -0.6994,  0.2260],
        [-0.1172, -0.3522, -0.7584,  0.1804]], grad_fn=<ScatterAddBackward>)

3.3 Edge Convolution 边卷积层的实现

边卷积层的数学定义如下：

x i ( k ) = max ? j ∈ N ( i ) h Θ ( x i ( k ? 1 ) , x j ( k ? 1 ) ? x i ( k ? 1 ) ) x_i^{(k)}=\max_{j \in N(i)} h_{\Theta}(x_i^{(k-1)},x_j^{(k-1)}-x_i^{(k-1)})

为多层感知机，类似于GCN，边卷积层同样继承于于基础类MessagePassing，不同在于采用max函数作为

□ \square

□函数。

边卷积层的主要理论来自于论文Dynamic Graph CNN for Learning on Point Clouds，这篇文章提出一种边卷积（EdgeConv）操作，来完成点云中点与点之间关系的建模，使得网络能够更好地学习局部和全局特征。具体可以看这两篇博客：【深度学习——点云】DGCNN(EdgeConv)和论文笔记：DGCNN（EdgeConv）。

import torch
from torch.nn import Sequential as Seq, Linear, ReLU
from torch_geometric.nn import MessagePassing

class EdgeConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super(EdgeConv, self).__init__(aggr=‘max‘) #  "Max" aggregation.
        self.mlp = Seq(Linear(2 * in_channels, out_channels),
                       ReLU(),
                       Linear(out_channels, out_channels))

    def forward(self, x, edge_index):
        # x has shape [N, in_channels]
        # edge_index has shape [2, E]

        return self.propagate(edge_index, x=x)

    def message(self, x_i, x_j):
        # x_i has shape [E, in_channels]
        # x_j has shape [E, in_channels]

        tmp = torch.cat([x_i, x_j - x_i], dim=1)  # tmp has shape [E, 2 * in_channels]
        return self.mlp(tmp)

边缘卷积实际上是一种动态卷积，它使用特征空间中的最近邻重新计算每一层的图。PyTorch geometry附带一个GPU加速的批处理k-NN图形生成方法——torch_geometric.n .pool.knn_graph()。

from torch_geometric.nn import knn_graph

class DynamicEdgeConv(EdgeConv):
    def __init__(self, in_channels, out_channels, k=6):
        super(DynamicEdgeConv, self).__init__(in_channels, out_channels)
        self.k = k

    def forward(self, x, batch=None):
        edge_index = knn_graph(x, self.k, batch, loop=False, flow=self.flow)
        return super(DynamicEdgeConv, self).forward(x, edge_index)

4. 建立自己的数据集

PyTorch Geometric提供了两个抽象类——torch_geometric.data.Dataset和torch_geometric.data.InMemoryDataset。前者适用于不能一次性放进内存中的大数据集，后者适用于可以全部放进内存中的小数据集。

4.1 “In Memory Datasets”的创建

torch_geometric.data.InMemoryDataset有四个可选参数：

root (string, optional) ——保存数据集的根目录。每个数据集都传递一个根文件夹，该根文件夹指示数据集应该存储在何处。将根文件夹分成两个文件夹：未处理过的数据集被保存在raw_dir目录下；已处理的数据集被保存在processed_dir目录下。
transform (callable, optional)
pre_transform (callable, optional)
pre_filter (callable, optional)

建立In Memory Datasets，需要用到四个基本的方法：

raw_file_names()——返回一个包含所有未处理过的数据文件的文件名的列表。
processed_file_names()——返回一个包含所有处理过的数据文件的文件名的列表。
download()——下载数据到raw_dir目录下。
process()——对数据的处理函数，是核心的函数之一。

下面是官方文档给出的一个示例：

import torch
from torch_geometric.data import InMemoryDataset


class MyOwnDataset(InMemoryDataset):
    def __init__(self, root, transform=None, pre_transform=None):
        super(MyOwnDataset, self).__init__(root, transform, pre_transform)
        self.data, self.slices = torch.load(self.processed_paths[0])

    @property
    def raw_file_names(self):
        return [‘some_file_1‘, ‘some_file_2‘, ...]

    @property
    def processed_file_names(self):
        return [‘data.pt‘]

    def download(self):
        # Download to `self.raw_dir`.

    def process(self):
        # Read data into huge `Data` list.
        data_list = [...]

        if self.pre_filter is not None:
            data_list = [data for data in data_list if self.pre_filter(data)]

        if self.pre_transform is not None:
            data_list = [self.pre_transform(data) for data in data_list]

        data, slices = self.collate(data_list)
        torch.save((data, slices), self.processed_paths[0])

4.2 创建更大的数据集

对于无法全部放进内存中的大数据集，可以使用torch_geometric.data.Dataset。torch_geometric.data.Dataset的参数和torch_geometric.data.InMemoryDataset的一致。常用的方法如下：

len()——获取数据集中的数据量。
get(idx)——获取索引为idx的数据对象。