In our last example, we explored the scheduling of 2 factories.
Both factories had 2 costs:
Fixed Costs - Costs incurred while the factory is running
Variable Costs - Cost per unit of production
We‘re going to introduce a third cost - Start up cost.
This will be a cost incurred by turning on the machines at one of the factories.
In this example, our start-up costs will be:
Factory A - €20,000
Factory B - €400,000
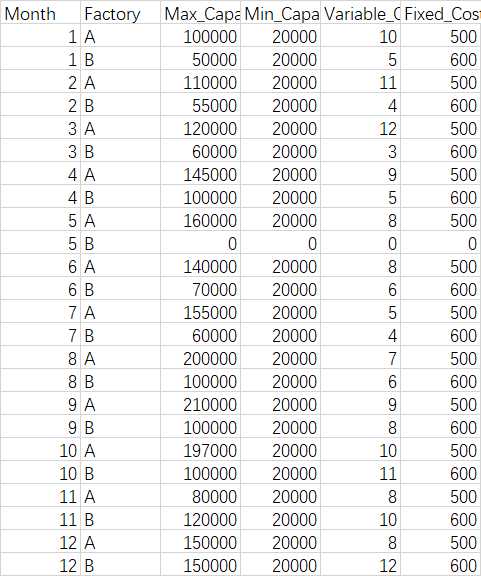
Let‘s start by reminding ourselves of the input data.
factory_variables.csv
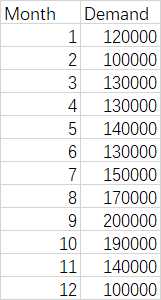
monthly_demand.csv
# -*- coding: utf-8 -*-
"""
Created on Mon Sep 14 14:35:48 2020
@author: juncheng
程序功能:
有两类成本:
固定成本--只要这个厂开工就会有的固定的成本
可变成本--每生产一个产品就会花费的成本,每个月都是变化的
现在我们再增加一个启动成本,也就是一个工程停工后在开工就会增加额外的启动成本。
A厂和B厂的启动成本分别是€20,000和€400,000。
"""
import pandas as pd
import pulp
factories = pd.read_csv(‘factory_variables.csv‘, index_col=[‘Month‘, ‘Factory‘])
demand = pd.read_csv(‘monthly_demand.csv‘, index_col=[‘Month‘])
# 产量
production = pulp.LpVariable.dicts("production",
((month, factory) for month, factory in factories.index),
lowBound=0,
cat=‘Integer‘)
‘‘‘
production
{(1, ‘A‘): production_(1,_‘A‘),
(1, ‘B‘): production_(1,_‘B‘),
(2, ‘A‘): production_(2,_‘A‘),
...
(12, ‘B‘): production_(12,_‘B‘)}
‘‘‘
# 工厂的状态,开工或者停工
factory_status = pulp.LpVariable.dicts("factory_status",
((month, factory) for month, factory in factories.index),
cat=‘Binary‘)
‘‘‘
factory_status
{(1, ‘A‘): factory_status_(1,_‘A‘),
(1, ‘B‘): factory_status_(1,_‘B‘),
(2, ‘A‘): factory_status_(2,_‘A‘),
(2, ‘B‘): factory_status_(2,_‘B‘),
(3, ‘A‘): factory_status_(3,_‘A‘),
...
(12, ‘B‘): factory_status_(12,_‘B‘)}
‘‘‘
# 工厂是否启动状态
switch_on = pulp.LpVariable.dicts("switch_on",
((month, factory) for month, factory in factories.index),
cat=‘Binary‘)
‘‘‘
{(1, ‘A‘): switch_on_(1,_‘A‘),
(1, ‘B‘): switch_on_(1,_‘B‘),
(2, ‘A‘): switch_on_(2,_‘A‘),
(2, ‘B‘): switch_on_(2,_‘B‘),
...
(12, ‘B‘): switch_on_(12,_‘B‘)}
‘‘‘
#接下来定义问题和目标函数:
# 初始化模型model
model = pulp.LpProblem("scheduling_problem", pulp.LpMinimize)
# 选择工厂A的索引
factory_A_index = [tpl for tpl in factories.index if tpl[1] == ‘A‘]
factory_B_index = [tpl for tpl in factories.index if tpl[1] == ‘B‘]
# 定义目标函数
model += pulp.lpSum(
[production[m, f] * factories.loc[(m, f), ‘Variable_Costs‘] for m, f in factories.index]
+ [factory_status[m, f] * factories.loc[(m, f), ‘Fixed_Costs‘] for m, f in factories.index]
+ [switch_on[m, f] * 20000 for m, f in factory_A_index]
+ [switch_on[m, f] * 400000 for m, f in factory_B_index]
)
#factory_A_index是工厂A的索引,它的值为:
#[(1, ‘A‘), (2, ‘A‘), (3, ‘A‘), (4, ‘A‘), (5, ‘A‘), (6, ‘A‘), # (7, ‘A‘), (8, ‘A‘), (9, ‘A‘), (10, ‘A‘), (11, ‘A‘), (12, ‘A‘)]
#除了固定成本和可变成本外,现在多了一个启动成本,A厂的启动成本是20000,B厂是400000。
#然后是定义约束,我们先把前面的约束都照抄过来:
# 产量等于需求量
months = demand.index
for month in months:
model += production[(month, ‘A‘)] + production[(month, ‘B‘)] == demand.loc[month, ‘Demand‘]
# 如果停工,产量为0,否则产量在最大和最小产能之间。
for month, factory in factories.index:
min_production = factories.loc[(month, factory), ‘Min_Capacity‘]
max_production = factories.loc[(month, factory), ‘Max_Capacity‘]
model += production[(month, factory)] >= min_production * factory_status[month, factory]
model += production[(month, factory)] <= max_production * factory_status[month, factory]
# B厂五月份停工
model += factory_status[5, ‘B‘] == 0
model += production[5, ‘B‘] == 0
#现在我们需要定义switch_on,也就是是否有启动成本了。根据问题,如果上个月的状态factory_status是0并且本月是1,则switch_on是1,否则switch_on是0。也就是:
‘‘‘
if factory_status[month - 1] == 0 and factory_status[month] == 1:
switch_on[month] = 1
else:
switch_on[month] = 0
但是第一个月的情况需要特殊处理,虽然Python的”-1”下标表示最后一个元素从而不会有下标越界的问题,但是我们最好谨慎处理。
But now we want to add in our constraints for switching on.
A factory switches on if:
It is off in the previous month (m-1)
AND it on in the current month (m).
As we don‘t know if the factory is on before month 0, we‘ll assume that the factory has switched on if it is on in month 1.
‘‘‘
for month, factory in factories.index:
# 我们假设第0个月是没有开工的,因此第一个月如果开工就有启动成本,否则没有
if month == 1:
model += switch_on[month, factory] == factory_status[month, factory]
else:
model += switch_on[month, factory] >= factory_status[month, factory] - factory_status[month-1, factory]
model += switch_on[month, factory] <= 1 - factory_status[month-1, factory]
model += switch_on[month, factory] <= factory_status[month, factory]
‘‘‘
For those interested in using my function defined above (make_io_and_constraint). Instead of:
model += switch_on[month, factory] >= factory_status[month, factory] - factory_status[month-1, factory]
model += switch_on[month, factory] <= 1 - factory_status[month-1, factory]
model += switch_on[month, factory] <= factory_status[month, factory]
You could write:
for constraint in make_io_and_constraint(switch_on[month, factory],
factory_status[month, factory],
factory_status[month-1, factory], 0, 1):
model += constriant
我们这里使用了函数make_io_and_constraint,它表达的约束就是:如果上个月的状态factory_status是0并且本月是1,则switch_on是1,否则switch_on是0。
def make_io_and_constraint(y1, x1, x2, target_x1, target_x2):
"""
Returns a list of constraints for a linear programming model
that will constrain y1 to 1 when
x1 = target_x1 and x2 = target_x2;
where target_x1 and target_x2 are 1 or 0
"""
binary = [0,1]
assert target_x1 in binary
assert target_x2 in binary
if IOx1 == 1 and IOx2 == 1:
return [
y1 >= x1 + x2 - 1,
y1 <= x1,
y1 <= x2
]
elif IOx1 == 1 and IOx2 == 0:
return [
y1 >= x1 - x2,
y1 <= x1,
y1 <= (1 - x2)
]
elif IOx1 == 0 and IOx2 == 1:
return [
y1 >= x2 - x1,
y1 <= (1 - x1),
y1 <= x2
]
else:
return [
y1 >= - (x1 + x2 -1),
y1 <= (1 - x1),
y1 <= (1 - x2)
]
‘‘‘
#约束定义完成之后剩下就是求解和输出结果了:
model.solve()
print(pulp.LpStatus[model.status])
output = []
for month, factory in production:
var_output = {
‘Month‘: month,
‘Factory‘: factory,
‘Production‘: production[(month, factory)].varValue,
‘Factory Status‘: factory_status[(month, factory)].varValue,
‘Switch On‘: switch_on[(month, factory)].varValue
}
output.append(var_output)
output_df = pd.DataFrame.from_records(output).sort_values([‘Month‘, ‘Factory‘])
output_df.set_index([‘Month‘, ‘Factory‘], inplace=True)
print(output_df)
print(pulp.value(model.objective))
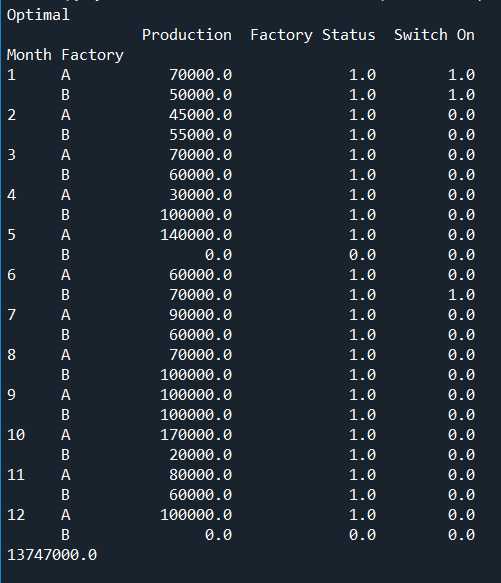
运行结果:
Pulp之三:官网上的应用样例(5)-Scheduling of 2 factories (工厂生产问题) (双索引的用法)
原文:https://www.cnblogs.com/treasury-manager/p/13800500.html