Magic circle (ring)

Description

\(\text{Smart}\) has \(1\) magic rings and \(n\) magic beads. Some magic beads have a "mysterious connection". Now you need to place these \(n\) magic beads on the magic ring. There are two magic beads placed in the same position. If you regard magic beads as points and "mysterious connections" as edges, then magic beads and mysterious connections will form a tree. After you place magic beads, if any two edges intersect, the intersection must be at the vertex, otherwise Disastrous consequences will occur.
Now you are required to find how many ways to place the magic orbs to meet the requirements without causing catastrophic consequences.

Format

Input

A positive integer \(n\) in the first line means that there are \(n\) magic beads;
In the next \(n-1\) line, each line has two positive integers \(x, y\), representing the "mysterious connection" between the magic bead numbered \(x\) and the magic bead numbered \(y\).

Output

An integer on a line represents the number of legal schemes, and the answer is modulo \(998244353\).

Sample

Input

4
1 2
1 3
2 4

Output

16

Sample Explanation

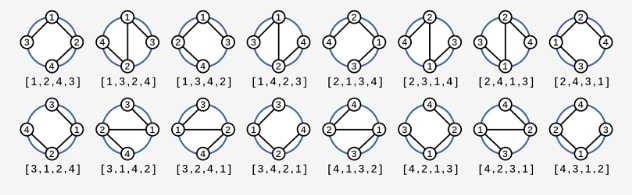
For example: There is a mysterious connection between \(n=4, (1,2) (1,3) (2,4)\), then the number of legal schemes is \(16\), and the legal schemes are shown in the figure below:

Hint

\(30\%\) data: \(n \le 9\);
Another \(30\%\) data: the tree given is a chain, \(n \le=200000\);
Data for \(100\%\): \(n \le 200000\).

Sample Code

Code is not available!

Magic circle (ring)

原文：https://www.cnblogs.com/jiupinzhimaguan/p/13817411.html