根据分布值得到累计密度函数,例如分布值为1,则累计密度为:
0.5 + 0.841344746068543 ≈ 0.841 也就是当标准差位于+1时候的累计密度。
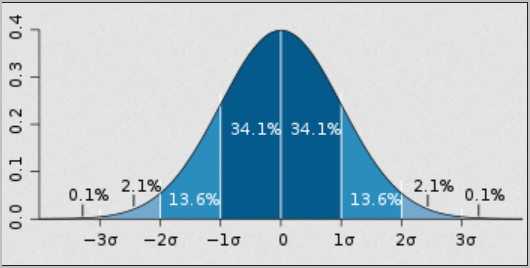
正太分布中+1个标准差的面积概率是:34.1%
正太分布中+2个标准差的面积概率是:13.6%
正太分布中+3个标准差的面积概率是:2.1%
剩余部分的概率是:0.1%
在坐标轴的右边部分,合计的概率值是50%
NORM.S.DIST () 和 NORM.DIST ()是excel 提供的两个函数,用于求正态分布下累计概率面积及曲线上对应的概率值,避免将正态分布标准化及查询标准正态分布概率表。
NORM.S.DIST 函数
返回标准正态分布函数(该分布的平均值为 0,标准差为 1)。可以使用此函数代替标准正态曲线面积表。
语法 - 标准正态分布
NORM.S.DIST(z,cumulative)
NORM.S.DIST 函数语法具有下列参数:
Z 必需。 需要计算其分布的数值。
cumulative 必需。 Cumulative 是决定函数形式的逻辑值。 如果 cumulative 为 TRUE,则 NORMS.DIST 返回累积分布函数;如果为 FALSE,则返回概率密度函数。
例子:需要求标准正态分布下,z=0.28对应的概率,即标准正态分布下小于或等于z的曲线下的面积。
查表:
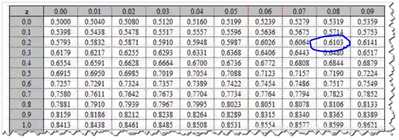
使用Excel函数验证是否准确:
NORM.S.DIST函数
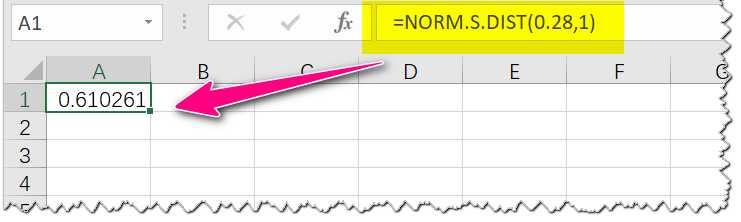
NORMSDIST(兼容Excel 2007与早期版本)
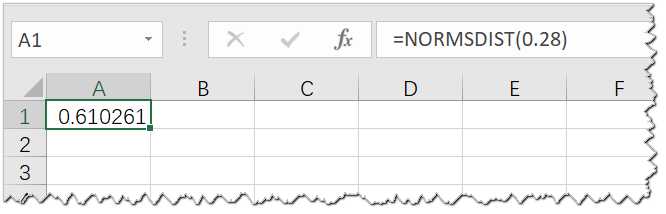
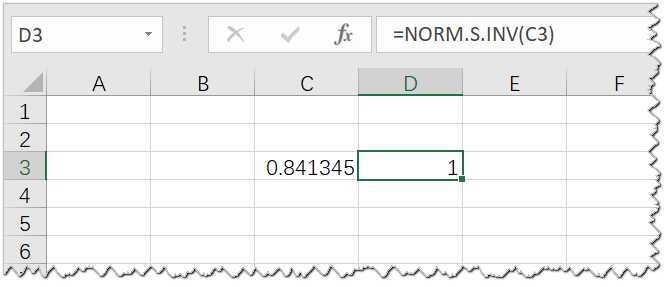
正太分布的反函数表示的是根据累计密度求出标准差,例如累计密度为:0.841344746068543,则标准差为+1个标准差。
NORM.S.INV函数
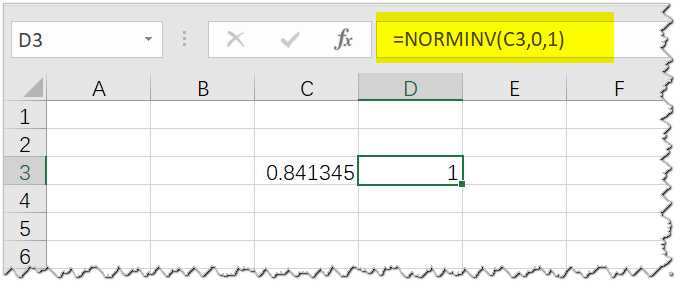
NORMINV函数(早期版本兼容)
原文:https://www.cnblogs.com/OliverQin/p/13829766.html