一个整数n(n <= 30)可以有多种分划，分划的整数之和为n，在不区分分划出各整数的次序时，字典序递减输出n 的各详细分划方案和分划总数。
----> : 例如n = 6，程序输出为：
6
5 1
4 2
4 1 1
3 3
3 2 1
3 1 1 1
2 2 2
2 2 1 1
2 1 1 1 1
1 1 1 1 1 1
total = 11
dfs:
sum记录当前划分之和，ans记录可分化的个数，dq用来存储我们一次分划中产生的数字；（不过这个过程中重复了很多步骤，当然因为要输出分划的数字，想来是不可避免，如果只是记录total,可选择动态规划，见后面）
dfs想法：从本身逐渐减小，同时sum进行判断，大于sum进行枝剪，小于则可以继续划分，等于则可以直接输出（优先队列便于操作）；
#include <iostream> #include <deque> #include <algorithm> using namespace std; int sum = 0, nn = 0, ans = 0; deque<int> dq; // 便于删除插入遍历 void dfs(int n) { // 深度优先搜索，从 nn -> 1 for (int i = n; i >= 1; i--) { // 从nn往下遍历 dq.push_back(i); sum += i; if (sum > nn) { // 剪枝 sum -= i; dq.pop_back(); } else if (sum == nn) { // 输出 deque<int>::iterator it; for (it = dq.begin(); it != dq.end(); it++) if (it == dq.begin()) cout << *it; else cout << " + " << *it; cout << endl; sum -= i; ans++; dq.pop_back(); } else { // 深度搜索 dfs(i); sum -= i; dq.pop_back(); } } } int main() { cout << "please input nn : "; cin >> nn; dfs(nn); cout << "total = " << ans << endl; return 0; }
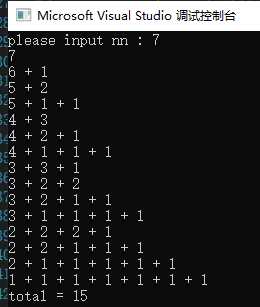（这个怎么把它放成横着的。。。。）
动态规划（total）：
#include <iostream> #include <cstring> using namespace std; int dp[7][7] = { 0 }; void Split(int n, int k) { for (int i = 1; i <= n; i++) { for (int j = 1; j <= k; j++) { if (i == 1 || j == 1) dp[i][j] = 1; else if (i < j) dp[i][j] = dp[i][i]; else if (i == j) dp[i][j] = dp[i][j - 1] + 1; else dp[i][j] = dp[i][j - 1] + dp[i - j][j]; } } } int main() { int n, k; cin >> n >> k; memset(dp, 0, sizeof(dp)); Split(n, k); cout << dp[n][k] << endl; return 0; }
2020-10-20
原文：https://www.cnblogs.com/2015-16/p/13849839.html