索引是帮助数据库高效获取数据的排好序的数据结构
也称二叉查找树,具有以下特征:
1)如果左子树不空,则左子树上所有结点关键字值均小于根结点关键字的值;
2)如果右子树不空,则右子树上所有结点关键字值均大于根结点关键字的值;
3)左右子树分别又是一颗二叉排序树。
将给定值与根节点进行比较,如果等于根节点,则查找成功;如果给定值比根节点的值小,则在左子树中查找;如果给定值比根节点大则在右子树中查找。
1 typedef struct BSTNode{ 2 int val; 3 struct BSTNode *lchlid; 4 struct BSTNode *rchild; 5 }BSTNode; 6 7 BSTNode *BST_Search(BSTree *T,int key,BSTNode *p) 8 { 9 p=NULL 10 while(T!=NULL&&T->val!=key) 11 { 12 p=T; //p为被查找结点的双亲 13 if(key<T->val) T=T->lchlid; 14 else 15 T=T->rchild; 16 } 17 return T; 18 }
1 #include<stdio.h> 2 #include<stdlib.h> 3 typedef struct BSTNode{ 4 int val; 5 struct BSTNode *lchlid; 6 struct BSTNode *rchild; 7 }BSTNode; 8 int BST_Insert(BSTNode **T, int key) 9 { 10 if ((*T) == NULL) 11 { 12 *T = (BSTNode*)malloc(sizeof(BSTNode)); 13 (*T)->val = key; 14 (*T)->lchlid = NULL; 15 (*T)->rchild = NULL; 16 return 1; 17 } 18 19 else if (key == (*T)->val) 20 return 0; 21 else if (key<(*T)->val) 22 return BST_Insert(&((*T)->lchlid), key); 23 else if (key>(*T)->val) 24 return BST_Insert(&((*T)->rchild), key); 25 } 26 //递归方式创建一个二叉排序树 27 void Creat_BST(BSTNode **T, int a[], int len) 28 { 29 int i = 0; 30 while (i<len) 31 { 32 BST_Insert(T, a[i]); 33 i++; 34 } 35 } 36 37 int main() 38 { 39 int a[5] = { 4, 8, 1, 9, 3 }; 40 BSTNode *T = NULL; 41 //如果想要在子函数中修改一级指针的指向,需要传递二级指针,C语言简直在裸奔┭┮﹏┭┮ 42 Creat_BST(&T, a, 5); 43 system("pause"); 44 45 }
上面例子中的数字,组成的二叉树刚好是平衡,即左右子树的高度差的绝对值不超过1,对其查找的时间复杂度在最坏情况下是O(log2n),但是如果我们把a数组改为{3,5,6,8,9},该树就退化成了一个链表,时间复杂度为O(n)
红黑树是一种自平衡二叉查找树,是对AVL(平衡二叉查找树)的改进,由于左右子树高度差的绝对值不超过1,所以对其进行查找、删除、插入在平均和最坏的情况下都是O(log2n),但是AVL树在插入和删除的过程中需要调整多次才能达到平衡。而红黑树相较于AVL的时间复杂度是一样的,红黑树牺牲掉了部分平衡性达到了减少旋转次数,总的来说黑红树性能优于AVL树。
红黑树的性质:
1、根是黑色;
2、每个红色结点必须有两个黑色结点;
3、从任意结点到其每个叶子结点的简单路径都包含相同数量的黑色结点;
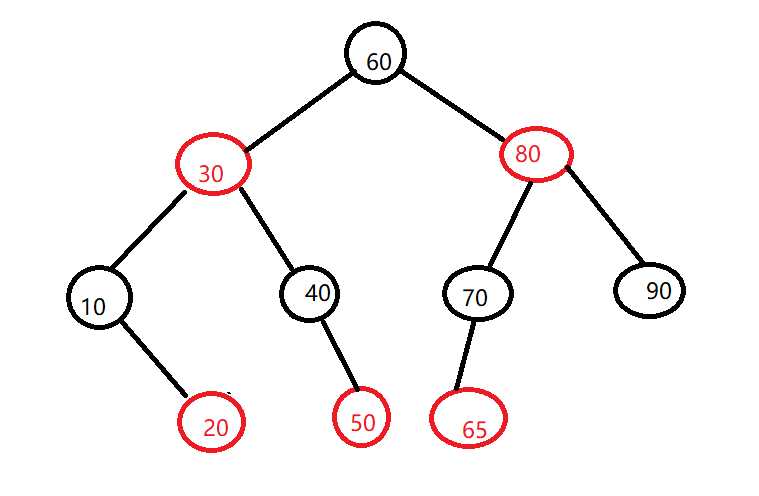
创建一颗红黑树
红黑树的结构
#define RED 0 #define BLACK 1 typedef struct RBTreeNode{ char color; int key; struct RBTreeNode *left, *right, *parent; }Node, *RBTree; //红黑树的根 typedef struct rb_root{ Node *node; }RBRoot;
创建一颗红黑树需要理解以下五种情况:
case1:只有新节点一个结点,新节点没有父节点,直接将新节点标记为黑色。
case2:新节点的父节点是黑色,新节点默认插入是红色,满足以上性质。
case3:新节点的父节点是红色,叔叔结点存在且是红色,把新节点的父节点和叔叔结点标记为黑色,并把祖父结点标记为红色,把祖父结点当成新节点继续判断。
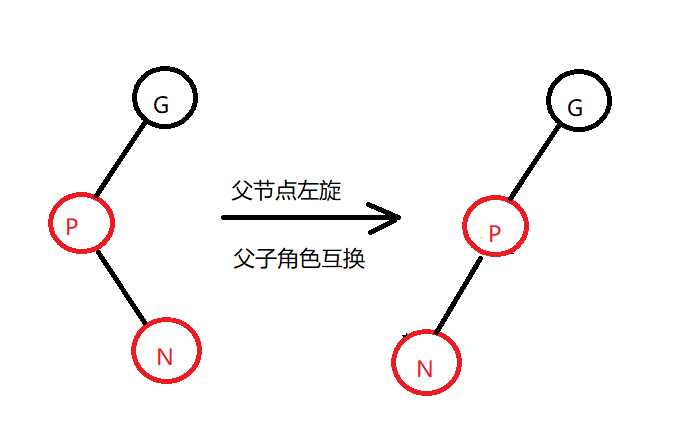
case4:新节点的父节点是红色,且叔叔不存在或者叔叔是黑色,并且新节点是其父节点的右孩子,而父节点又是祖父结点的左孩子。对父节点进行左旋,互换父子角色。
case5:新节点的父节点是红色,且叔叔不存在或者叔叔是黑色,并且新节点是其父节点的左孩子,而父节点又是祖父结点的左孩子。把祖父结点改为红色,把父节点改为黑色,对其祖父进行右旋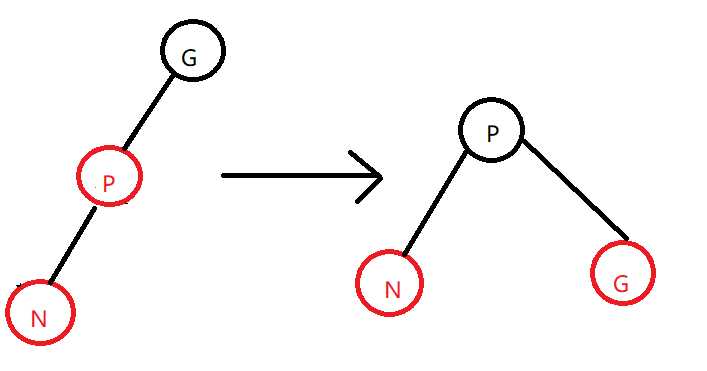
1 //.c 2 //创建红黑树,返回根 3 RBRoot *Create_rbtree(){ 4 RBRoot *root = (RBRoot*)malloc(sizeof(RBRoot)); 5 root->node = NULL; 6 return root; 7 } 8 //左旋 9 void rbtree_left_rotate(RBRoot *root, Node *x){ 10 //设置x的右孩子为y 11 Node *y = x->right; 12 //y的左孩子设为x的右孩子 13 //if y的左孩子不为空,将x设为y的左孩子的父亲 14 x->right = y->left; 15 if (y->left) 16 { 17 y->left->parent = x; 18 } 19 //将x的父亲设为y的父 20 y->parent = x->parent; 21 if (x->parent==NULL) 22 { 23 root->node = y; 24 } 25 else 26 { 27 if (x->parent->left==x) 28 {//如果x是父节点的左孩子,将y设为x的父节点的左孩子 29 x->parent->left = y; 30 31 } 32 else 33 { 34 x->parent->right = y; 35 } 36 } 37 //将x设为y的左孩子 38 y->left = x; 39 //将x的父节点设为y 40 x->parent = y; 41 } 42 void rbtree_right_rotate(RBRoot *root, Node *y){ 43 Node*x = y->left; 44 y->left = x->right; 45 if (x->right) 46 { 47 x->right->parent = y; 48 } 49 x->parent = y->parent; 50 if (y->parent==NULL) 51 { 52 root->node = x; 53 } 54 else 55 { 56 if (y==y->parent->right) 57 { 58 y->parent->right = x; 59 } 60 else 61 { 62 y->parent->left = x; 63 } 64 } 65 x->right = y; 66 y->parent = x; 67 } 68 void rbtree_fixup(RBRoot*root, Node* node){ 69 Node *parent, *gparent; 70 //如果父节点存在,并且父节点是红色 71 while ((parent=node->parent)&&(parent->color==RED)) 72 { 73 gparent = parent->parent; 74 //如果父节点是祖父节点的左孩子 75 if (parent == gparent->left){ 76 //case1:叔叔节点是红色 77 { 78 Node*nucle = gparent->right; 79 if (nucle &&(nucle->color==RED)) 80 { 81 nucle->color = BLACK; 82 parent->color = BLACK; 83 gparent->color = RED; 84 node = gparent; 85 continue; 86 87 } 88 } 89 //case2:叔叔是黑色或者不存在,当前节点是右孩子 90 if (parent->right == node){ 91 Node *temp; 92 rbtree_left_rotate(root, parent); 93 temp = parent; 94 parent = node; 95 node = temp; 96 } 97 //case3 :叔叔是黑色,且当前节点是左孩子 98 parent->color = BLACK; 99 gparent->color = RED; 100 rbtree_right_rotate(root, gparent); 101 } 102 else//若父节点是祖父节点的右孩子 103 { 104 //case1 条件 :叔叔节点是红色 105 Node *uncle = gparent->left; 106 if (uncle&&uncle->color==RED) 107 { 108 uncle->color = BLACK; 109 parent->color = BLACK; 110 gparent->color = RED; 111 node = gparent; 112 continue; 113 } 114 //case 2条件:叔叔是黑色,而且当前节点是左孩子 115 if (parent->left == node){ 116 Node *tmp; 117 rbtree_right_rotate(root, parent); 118 tmp = parent; 119 parent = node; 120 node = tmp; 121 } 122 //case3 :叔叔是黑色,且当前节点是右孩子。 123 parent->color = BLACK; 124 gparent->color = RED; 125 rbtree_left_rotate(root, gparent); 126 } 127 } 128 root->node->color = BLACK; 129 } 130 void rbtree_insert(RBRoot *root,Node *node){ 131 Node *q = NULL; 132 Node *p = root->node; 133 while (p) 134 { 135 q = p; 136 if (node->key<q->key) 137 { 138 p = p->left; 139 } 140 else 141 { 142 p = p->right; 143 } 144 } 145 node->parent = q;//q是要插入结点的父节点 146 if (q){ 147 if (node->key<q->key) 148 { 149 q->left = node; 150 } 151 else 152 { 153 q->right = node; 154 } 155 } 156 else 157 { 158 root->node = node; 159 } 160 node->color = RED;//红色 161 rbtree_fixup(root ,node); 162 163 164 } 165 void insert_rbtree(RBRoot*root, int key){ 166 Node *node = (Node*)malloc(sizeof(Node)); 167 node->key = key; 168 node->left = node->right = node->parent = NULL; 169 node->color = BLACK;//黑色 170 rbtree_insert(root, node); 171 }
红黑树的性能已经很高了。但是MySQL的底层索引还是没有选择红黑树。
原因:数据库中的数据量大,红黑树的高度不可控,由于MySQL中的索引也是存储在磁盘中,那么在查找过程中也要进行多次读取磁盘操作,势必会降低效率;再者,一次读取磁盘会读16K的数据,而红黑树的结点中只存储一个数据量,读取浪费。
B-Tree也称多路平衡查找树,一颗m阶B树,满足以下条件:
B+树是B树的变种,满足以下条件:
树中每个结点至多有m颗子树,至多有m关键字;
根节点至少有两棵子树;
除根结点以外的其他分支结点至少有ceil(m/2)颗子树,至少有ceil(m/2)个关键字;
所有叶子结点包含全部关键字以及指向相应记录的指针,叶子节点中将关键按照从小到大顺序排列,相邻叶子结点按照大小顺排序相互链接起来;
所有的分支结点中仅包含它的各个子结点中的关键字的最大值以及指向其子节点的指针;
了解了什么是B+树,我们对二叉排序树、红黑树、B+树在极端情况下进行比较
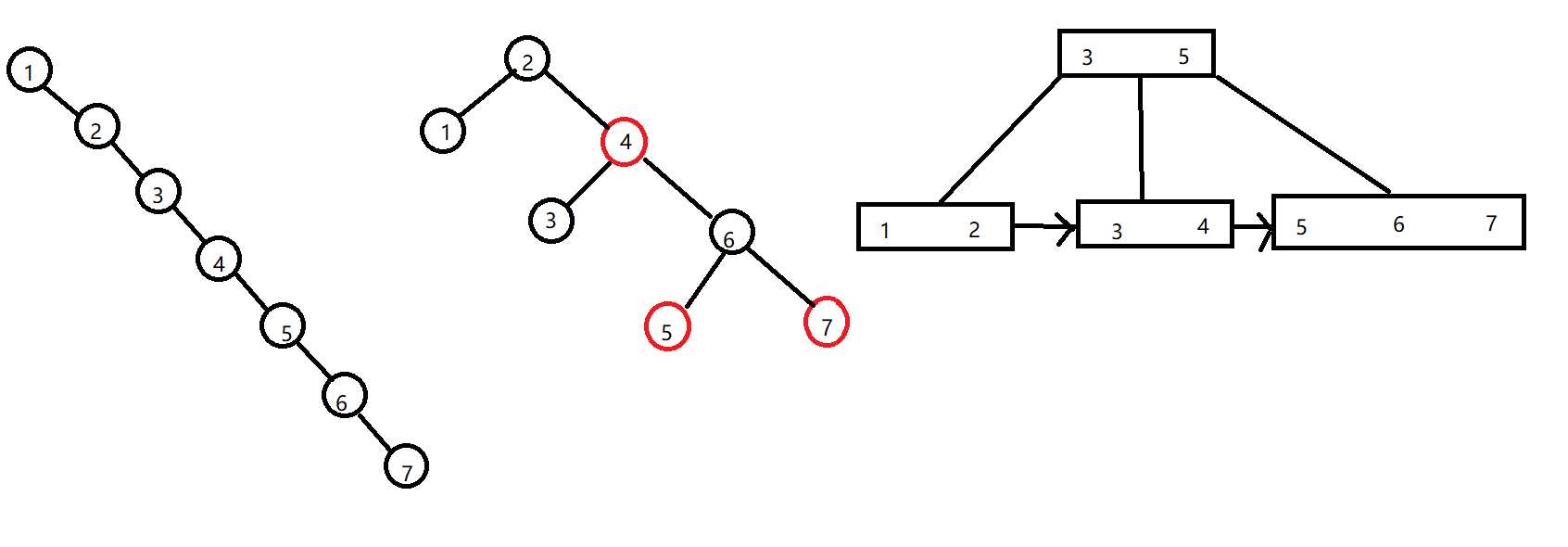
二叉排序中查找“6”需要查找6次,红黑树需要查找3次,B+树只需要查找两次,因为B+树的高度最低,那么数据库中有上千万条数据,B+树还能维持“矮高度”的优势吗?
在MYSQL数据库中,它给B+树中的结点设置大小为16KB,非叶子结点是由相同数量的关键字和指向子节点的指针组成,其中指针占6字节,假设结点中关键字是bigint类型(8字节),一个结点就能存1170个关键字(索引),叶子结点是由关键字和记录组成,一个关键字对应一条记录,一个关键字和一个记录加起来也不会超过1KB,叶子结点最少可以存放16个索引。那么一个高度为3的B+树一共能存储1170*1170*16=2190万个关键字。由于根节点的数据常驻内存,所以对一张千万级的数据表查询,也不过1~2次的IO操作。
原文:https://www.cnblogs.com/xiaoxiaolinux/p/13759482.html