最近看了相关的知识，搞懂了一些原理。就此次记录一下。

1.用齐次坐标系表示无穷远点

1.1无穷点坐标

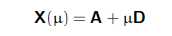
世界坐标系的X用四维坐标表示为：

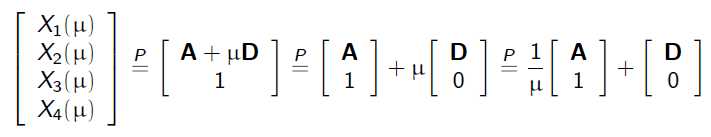 无穷点在图像上的投影：

1.2　两点成线，两线交点：

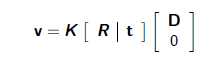
两点叉乘表示线（齐次坐标系下表示）：

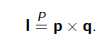
 证明：标量混合积 ： p$\cdot$I=p$\cdot$(p$\times$q)=0.

2.两点确定Epipolar Line

2.1 无穷点和光心

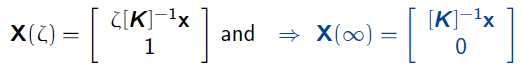
可以看到这里的齐次坐标的最后一个参数为0，即代表不穷远处的点。$[K]^-1$x代表平行线的方向向量（平行线在Eulidian坐标系下相交于无穷点）。

光心很简单就是：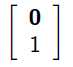

2.2 Epipole

一个相机的光心C投影到另一个相机，与其图像的交点即为Epipole。用坐标表示即为：

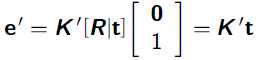
 相应的无穷远处点在原坐标系下向另一个相机坐标系投影为（原相机坐标系为世界坐标系）：

 2.3 Eipoplar Line

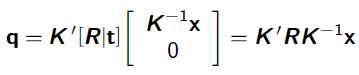
由上面的两点成线可知，即我的Eipoplar Line：I’=$e‘ \times q$=K‘t$K‘Rk^-1x$;使用公式(Ma)$\times$(Mb)=$M^-T$(a$\times$b)得：

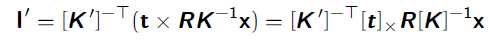
 其中，Fundamental Matrix就是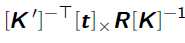，结合点在线上的公式可知可知（x‘在I’上）：$x‘^T$Fx=0；

Fundamental Matrix

原文：https://www.cnblogs.com/xsy123/p/13652312.html