本文先简要介绍三个乘子法,它们的收敛条件依次减弱(不做具体介绍),然后应用 ADMM 算法求解 Basis pursuit 问题最后读读 Boyd 给出的代码。
乘子法部分参考文献[1]。
考虑如下等式约束的优化问题
用拉格朗日乘子法求解,先写出拉格朗日函数:
其中 是拉格朗日乘子。它的对偶函数为
对偶问题为
我们需要的解是
这里的 是对偶问题的最优解,下面我们用梯度下降法求解它。迭代公式为
其中
①总结拉格朗日乘子法的更新方法如下:
用增广拉格朗日乘子法求解,先写出增广拉格朗日函数:
②类似拉格朗日乘子法,增广拉格朗日乘子法的更新方法如下:
ADMM 问题形式(with convex)
它的增广拉格朗日函数为
③ADMM 的更新方法如下:
优化目标:
写成 ADMM 的形式
其中 表示指示函数,相关的内容我在 [Opt] 近端最小化算法 有写过。那么它的增广拉格朗日函数为
第一步:更新 :
我们记 。上述问题为
在仿射集上的投影问题,求解参考[4],具体原理等内容我在 [ML] 深入线性回归 提到过。
它的解为 。
第二步:更新 :
上面这个问题我在 [Opt] Proximal Gradient 及 Lasso 问题 中详细讨论过了。它的解析解是
第三步,更新乘子
因此我们只要按如下等价地更新 即可
④ 总结 Basis pursuit 更新方法如下:
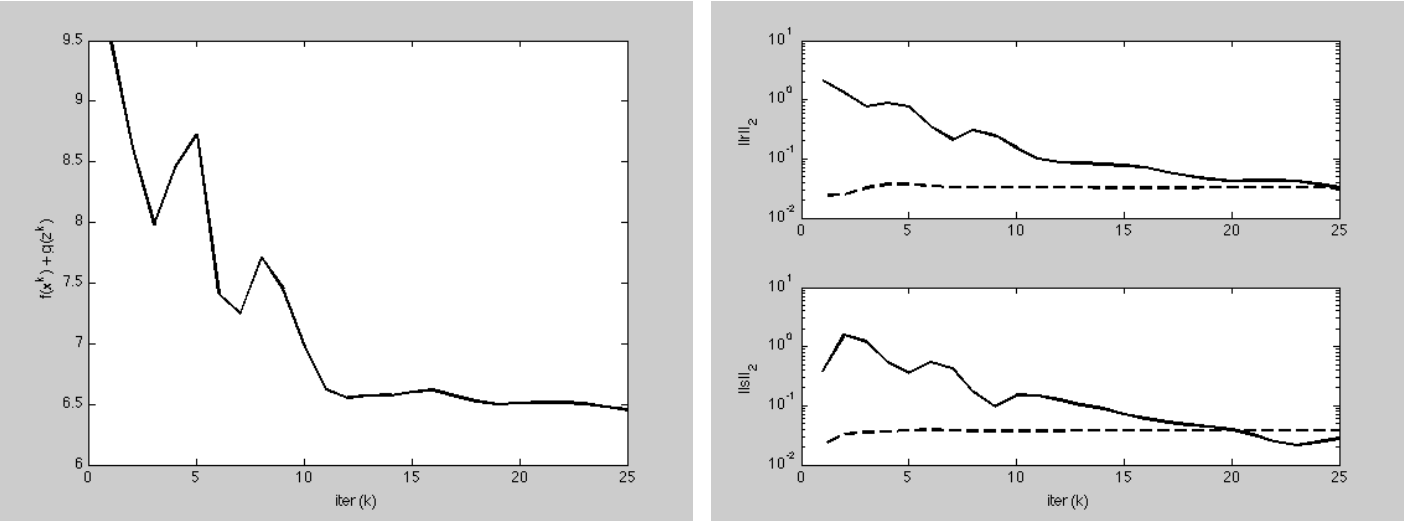
运行结果
左实线:目标函数值迭代更新变化曲线
右上实线:primal residual
右上虚线:primal feasibility tolerance
右下实线:dual residual
右下虚线:dual feasibility tolerance
MATLAB 中在命令行窗口输入如下指令获取 basis_pursuit 函数
grabcode("http://web.stanford.edu/~boyd/papers/admm/basis_pursuit/basis_pursuit.html")输入以下指令获取 Basis pursuit example 测试代码
grabcode("http://web.stanford.edu/~boyd/papers/admm/basis_pursuit/basis_pursuit_example.html")basis_pursuit.m
function [z, history] = basis_pursuit(A, b, rho, alpha)
% basis_pursuit Solve basis pursuit via ADMM
%
% [x, history] = basis_pursuit(A, b, rho, alpha)
%
% Solves the following problem via ADMM:
%
% minimize ||x||_1
% subject to Ax = b
%
% The solution is returned in the vector x.
%
% history is a structure that contains the objective value, the primal and
% dual residual norms, and the tolerances for the primal and dual residual
% norms at each iteration.
%
% rho is the augmented Lagrangian parameter.
%
% alpha is the over-relaxation parameter (typical values for alpha are
% between 1.0 and 1.8).
%
% More information can be found in the paper linked at:
% http://www.stanford.edu/~boyd/papers/distr_opt_stat_learning_admm.html
%
t_start = tic;
%% Global constants and defaults
QUIET = 0;
MAX_ITER = 1000;
ABSTOL = 1e-4; % 绝对误差容限
RELTOL = 1e-2; % 相对误差容限
%% Data preprocessing
[~, n] = size(A);
%% ADMM solver
x = zeros(n,1);
z = zeros(n,1);
u = zeros(n,1);
if ~QUIET
fprintf(‘%3s\t%10s\t%10s\t%10s\t%10s\t%10s\n‘, ‘iter‘, ...
‘r norm‘, ‘eps pri‘, ‘s norm‘, ‘eps dual‘, ‘objective‘);
end
% precompute static variables for x-update (projection on to Ax=b)
AAt = A*A‘;
P = eye(n) - A‘ * (AAt \ A);
q = A‘ * (AAt \ b);
for k = 1:MAX_ITER
% x-update
x = P*(z - u) + q;
% z-update with relaxation
zold = z;
x_hat = alpha*x + (1 - alpha)*zold; % 带松弛的更新方法
z = shrinkage(x_hat + u, 1/rho);
u = u + (x_hat - z);
% diagnostics, reporting, termination checks
history.objval(k) = objective(A, b, x);
history.r_norm(k) = norm(x - z); % primal residual
history.s_norm(k) = norm(