机器学习（线性模型）

线性模型

损失函数

源代码

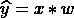
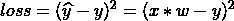
import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# our model for the forward pass
def forward(x):
    return x * w

# 损失函数
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)

#权重准备空列表
w_list = []
mse_list = []

for w in np.arange(0.0, 4.1, 0.1):
# Print the weights and initialize the lost
    print("w=", w)
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):

# For each input and output, calculate y_hat
# Compute the total loss and add to the total error
        y_pred_val = forward(x_val)#计算预测值
        l = loss(x_val, y_val)#计算损失
        l_sum += l
        print("\t", x_val, y_val, y_pred_val, l)
# Now compute the Mean squared error (mse) of each
# Aggregate the weight/mse from this run
    print("MSE=", l_sum / 3)#mse均方误差
    w_list.append(w)
    mse_list.append(l_sum / 3)

# Plot it all
plt.plot(w_list, mse_list)
plt.ylabel(‘Loss‘)
plt.xlabel(‘w‘)
plt.show()

结果

损失在w=2时为最小，为最优值

机器学习（线性模型）

原文：https://www.cnblogs.com/zhangqingqing24630/p/13888149.html