1. ranked retrieval
是free text queries形式,不需要query语言,直接输入要找的单词就可以
2. 做rank的前提是可以进行排序,如Jaccard Coefficient
jaccard(A, B) =|A∩B|/|A∪B|,即两者重复的单词数量比上二者总共的单词数量
jaccard(A, A)=1, jaccard(A, B)=0 if A∩B=0
但是这个方法并没有考虑一个单词出现的次数;很少出现的单词比大量出现的单词更具代表性,但是这个方法并没有考虑到这一点
3. bag of words model:将每句话打散成独立的单词,不关注单词出现的顺序
4. term frequency: tft,d指的是单词t在文章d中出现的次数
5. document frequency即一个单词在多少个文章中出现过;inverse document frequency即idf指的是log(N/dft),N是一共的文章数量,用它除去document frequency
单词出现的次数越少,idf越大
6. tf-idf weighting
![]()
对query与文章同时求tf-idf,然后求两者之间的差距
但是不能直接用欧几里得公式,要用下面的公式
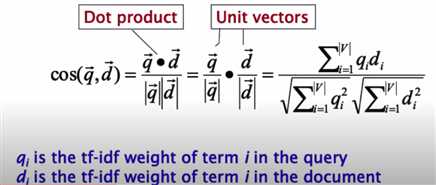
7. 计算cosine score的最后一步要除以length,即normalization;然后取top
简单理解就是对每一个query,求每个文章对应的score,取top
8. document使用lnc,代表log形式,no idf,用了cosine normalization
query使用ltc,代表log形式,使用idf,用了cosine normalization
9. effienct cosine ranking
快速计算+减少需要计算的数量
优化1:unweighted queries,即不对query本身进行计算,只看document本身,加快速度
优化2:max heap,binary tree的一种,父节点一定大于子节点,但是左右两个子节点的大小没有规定。构建的时间复杂度为O(n),找到前K个最大的值的复杂度为O(K*log(n)),因为每次遍历的时候走到最下面一层的复杂度为log(n),需要找到前K个
优化3:min heap,将最小的data放在最上面,即子节点总是大于父节点;tree形成之后,只要将位于root的最小的点pop掉就可以了;时间复杂度为O(n*log(k)+k*log(k))
10. query processing
document-at-a time:一个document一个document的处理,即对于query中的第一个term,首先处理array中的第一个文章,结束之后处理第二个。。。
term-at-a-time:一个term一个term的处理,首先处理inverted list中的第一个term,将出现该term的所有document都处理完再做别的term
第二个磁盘利用率更好一些
conjunctive TAAT:所有单词都出现在document中才能进入rank,只重合了一个单词不算
conjunctive DAAT:先做Boolean查找再做rank
11. maxscore methods:将每个term的最大值从大到小排序,假设要求top3,r‘是top3中最低的分数,若其中一个term的最大值比r‘要小
any doc scores higher than r‘ must contains at least one of the first 2 keywords
跳过个别单词
原文:https://www.cnblogs.com/eleni/p/13874752.html