一、简介
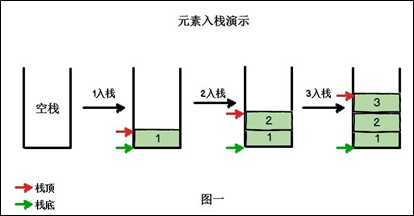
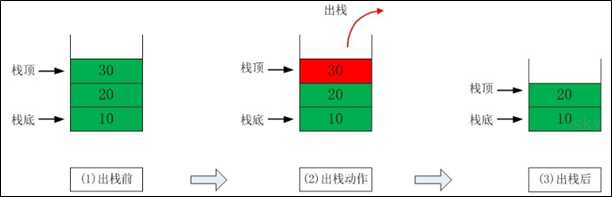
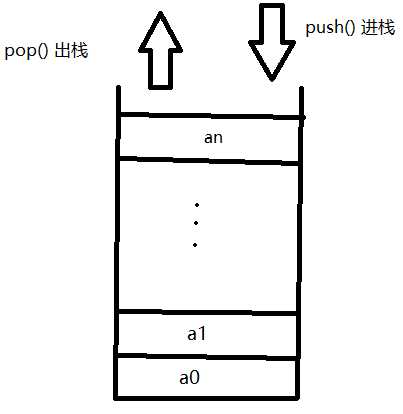
栈(英语:stack)又称为堆栈或堆叠,栈作为一种数据结构,是一种只能在一端进行插入和删除操作的特殊线性表。它按照先进后出的原则存储数据,先进入的数据被压入栈底(Bottom),最后的数据在栈顶(Top)。我们把插入元素的操作称为入栈(Push),删除元素的操作称为出栈(Pop)。
由于堆叠数据结构只允许在一端进行操作,因而按照后进先出(LIFO, Last In First Out)的原理运作。栈也称为后进先出表。
这里以羽毛球筒为例,羽毛球筒就是一个栈,刚开始羽毛球筒是空的,也就是空栈,然后我们一个一个放入羽毛球,也就是一个一个push进栈,当我们需要使用羽毛球的时候,从筒里面拿,也就是pop出栈,但是第一个拿到的羽毛球是我们最后放进去的。
栈的结构如下图:
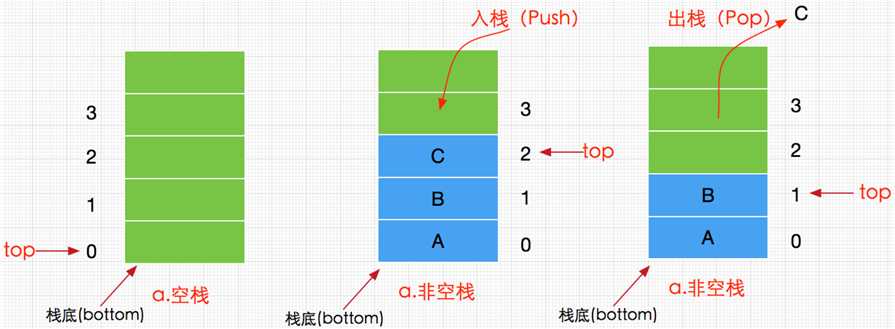
二、Java模拟简单的顺序栈实现
package com.ys.datastructure;
public class MyStack {
private int[] array;
private int maxSize;
private int top;
public MyStack(int size){
this.maxSize = size;
array = new int[size];
top = -1;
}
//压入数据
public void push(int value){
if(top < maxSize-1){
array[++top] = value;
}
}
//弹出栈顶数据
public int pop(){
return array[top--];
}
//访问栈顶数据
public int peek(){
return array[top];
}
//判断栈是否为空
public boolean isEmpty(){
return (top == -1);
}
//判断栈是否满了
public boolean isFull(){
return (top == maxSize-1);
}
}
测试:
package com.ys.test;
import com.ys.datastructure.MyStack;
public class MyStackTest {
public static void main(String[] args) {
MyStack stack = new MyStack(3);
stack.push(1);
stack.push(2);
stack.push(3);
System.out.println(stack.peek());
while(!stack.isEmpty()){
System.out.println(stack.pop());
}
}
}
结果:

这个栈是用数组实现的,内部定义了一个数组,一个表示最大容量的值以及一个指向栈顶元素的top变量。构造方法根据参数规定的容量创建一个新栈,push()方法是向栈中压入元素,指向栈顶的变量top加一,使它指向原顶端数据项上面的一个位置,并在这个位置上存储一个数据。pop()方法返回top变量指向的元素,然后将top变量减一,便移除了数据项。要知道 top 变量指向的始终是栈顶的元素。
产生的问题:
①、上面栈的实现初始化容量之后,后面是不能进行扩容的(虽然栈不是用来存储大量数据的),如果说后期数据量超过初始容量之后怎么办?(自动扩容)
②、我们是用数组实现栈,在定义数组类型的时候,也就规定了存储在栈中的数据类型,那么同一个栈能不能存储不同类型的数据呢?(声明为Object)
③、栈需要初始化容量,而且数组实现的栈元素都是连续存储的,那么能不能不初始化容量呢?(改为由链表实现)
三、增强功能版栈
对于上面出现的问题,第一个能自动扩容,第二个能存储各种不同类型的数据,解决办法如下:(第三个在讲链表的时候在介绍)
这个模拟的栈在JDK源码中,大家可以参考 Stack 类的实现。

package com.ys.datastructure;
import java.util.Arrays;
import java.util.EmptyStackException;
public class ArrayStack {
//存储元素的数组,声明为Object类型能存储任意类型的数据
private Object[] elementData;
//指向栈顶的指针
private int top;
//栈的总容量
private int size;
//默认构造一个容量为10的栈
public ArrayStack(){
this.elementData = new Object[10];
this.top = -1;
this.size = 10;
}
public ArrayStack(int initialCapacity){
if(initialCapacity < 0){
throw new IllegalArgumentException("栈初始容量不能小于0: "+initialCapacity);
}
this.elementData = new Object[initialCapacity];
this.top = -1;
this.size = initialCapacity;
}
//压入元素
public Object push(Object item){
//是否需要扩容
isGrow(top+1);
elementData[++top] = item;
return item;
}
//弹出栈顶元素
public Object pop(){
Object obj = peek();
remove(top);
return obj;
}
//获取栈顶元素
public Object peek(){
if(top == -1){
throw new EmptyStackException();
}
return elementData[top];
}
//判断栈是否为空
public boolean isEmpty(){
return (top == -1);
}
//删除栈顶元素
public void remove(int top){
//栈顶元素置为null
elementData[top] = null;
this.top--;
}
/**
* 是否需要扩容,如果需要,则扩大一倍并返回true,不需要则返回false
* @param minCapacity
* @return
*/
public boolean isGrow(int minCapacity){
int oldCapacity = size;
//如果当前元素压入栈之后总容量大于前面定义的容量,则需要扩容
if(minCapacity >= oldCapacity){
//定义扩大之后栈的总容量
int newCapacity = 0;
//栈容量扩大两倍(左移一位)看是否超过int类型所表示的最大范围
if((oldCapacity<<1) - Integer.MAX_VALUE >0){
newCapacity = Integer.MAX_VALUE;
}else{
newCapacity = (oldCapacity<<1);//左移一位,相当于*2
}
this.size = newCapacity;
int[] newArray = new int[size];
elementData = Arrays.copyOf(elementData, size);
return true;
}else{
return false;
}
}
}
测试:
//测试自定义栈类 ArrayStack
//创建容量为3的栈,然后添加4个元素,3个int,1个String.
@Test
public void testArrayStack(){
ArrayStack stack = new ArrayStack(3);
stack.push(1);
//System.out.println(stack.peek());
stack.push(2);
stack.push(3);
stack.push("abc");
System.out.println(stack.peek());
stack.pop();
stack.pop();
stack.pop();
System.out.println(stack.peek());
}
结果:

四、利用栈实现字符串逆序
我们知道栈是后进先出,我们可以将一个字符串分隔为单个的字符,然后将字符一个一个push()进栈,在一个一个pop()出栈就是逆序显示了。如下:
将 字符串“how are you” 反转!!!
这里我们是用上面自定的栈来实现的,大家可以将ArrayStack替换为JDK自带的栈类Stack试试
//进行字符串反转
@Test
public void testStringReversal(){
ArrayStack stack = new ArrayStack();
String str = "how are you";
char[] cha = str.toCharArray();
for(char c : cha){
stack.push(c);
}
while(!stack.isEmpty()){
System.out.print(stack.pop());
}
}
结果:

五、利用栈判断分隔符是否匹配
写过xml标签或者html标签的,我们都知道<必须和最近的>进行匹配,[ 也必须和最近的 ] 进行匹配。
比如:<abc[123]abc>这是符号相匹配的,如果是 <abc[123>abc] 那就是不匹配的。
对于 12<a[b{c}]>,我们分析在栈中的数据:遇到匹配正确的就消除
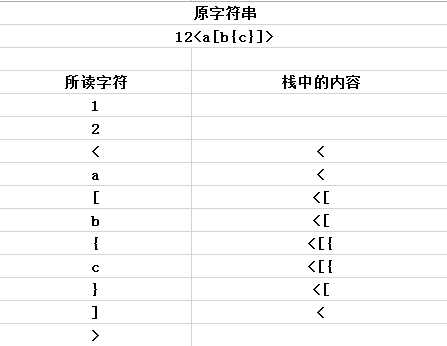
最后栈中的内容为空则匹配成功,否则匹配失败!!!
//分隔符匹配
//遇到左边分隔符了就push进栈,遇到右边分隔符了就pop出栈,看出栈的分隔符是否和这个有分隔符匹配
@Test
public void testMatch(){
ArrayStack stack = new ArrayStack(3);
String str = "12<a[b{c}]>";
char[] cha = str.toCharArray();
for(char c : cha){
switch (c) {
case ‘{‘:
case ‘[‘:
case ‘<‘:
stack.push(c);
break;
case ‘}‘:
case ‘]‘:
case ‘>‘:
if(!stack.isEmpty()){
char ch = stack.pop().toString().toCharArray()[0];
if(c==‘}‘ && ch != ‘{‘
|| c==‘]‘ && ch != ‘[‘
|| c==‘)‘ && ch != ‘(‘){
System.out.println("Error:"+ch+"-"+c);
}
}
break;
default:
break;
}
}
}
六、总结
根据栈后进先出的特性,我们实现了单词逆序以及分隔符匹配。所以其实栈是一个概念上的工具,具体能实现什么功能可以由我们去想象。栈通过提供限制性的访问方法push()和pop(),使得程序不容易出错。
对于栈的实现,我们稍微分析就知道,数据入栈和出栈的时间复杂度都为O(1),也就是说栈操作所耗的时间不依赖栈中数据项的个数,因此操作时间很短。而且需要注意的是栈不需要比较和移动操作,我们不要画蛇添足。
七、扩展
1、可查询最值的栈练习题
定义栈的数据结构,请在该类型中实现一个能够得到栈最小元素的min函数。
实现一个特殊的栈,再实现栈的基本功能的基础上,再实现返回栈中最小元素的操作getmin。
要求:
①pop、push、getmin的时间复杂度为O(1)。
②设计的栈类型可以使用现有的栈结构。
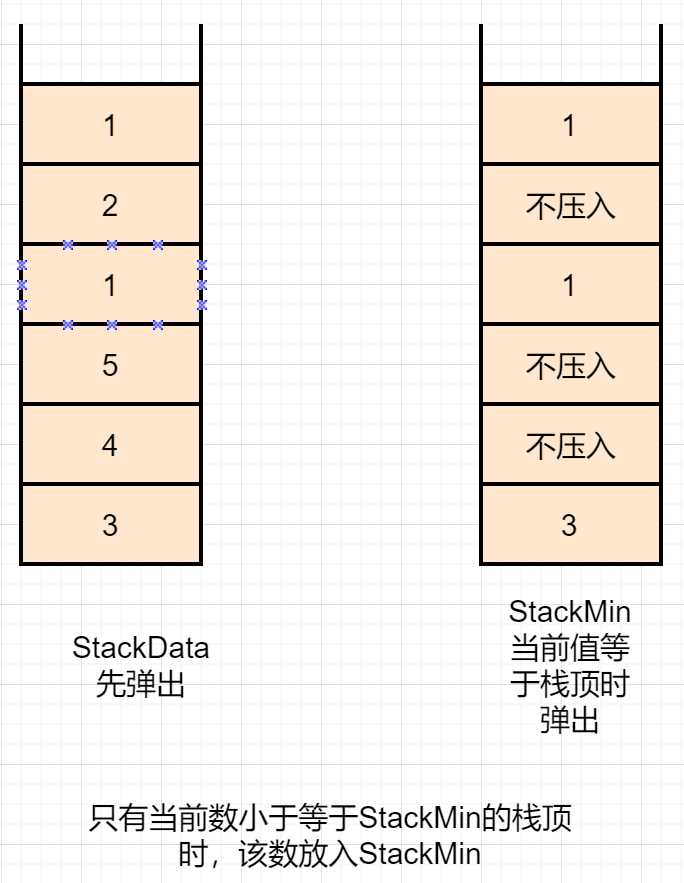
方法1
方法2
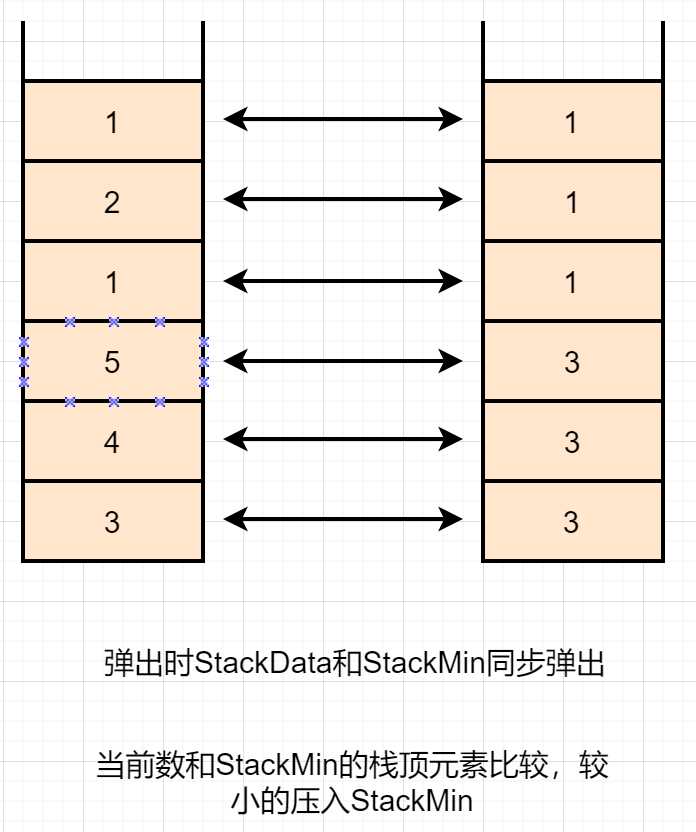
区别
1.方法1和方法2都是利用StackMin来保存每一步的最小值。
2.方法1和方法2的实现时间复杂度都是O(1)。
3.区别在于方法1稍省空间,略费时间,方法2则相反。
import java.util.Stack;
public class Solution {
private Stack<Integer> stackData = new Stack<>();
private Stack<Integer> stackMin = new Stack<>();
public void push(int node) {
//将当前元素压入栈
stackData.push(node);
/**
* 如果最小栈为空,那么直接压入
* 否则如果当前元素小于stackMin的顶部元素,直接压入,大于就继续压入stackMin的顶部元素
*/
if(stackMin.isEmpty()){
stackMin.push(node);
} else {
if (node < stackMin.peek().intValue()) {
stackMin.push(node);
}
else{
stackMin.push(stackMin.peek());
}
}
}
public void pop() {
stackData.pop();
stackMin.pop();
}
public int top() {
return stackData.peek();
}
public int min() {
return stackMin.peek();
}
}
2、栈的反转练习题
实现一个栈的逆序,但是只能用递归函数和这个栈本身的pop操作来实现,而不能自己申请另外的数据结构。
给定一个整数数组A即为给定的栈,同时给定它的大小n,请返回逆序后的栈。
测试样例:
[4,3,2,1],4
返回:
[1,2,3,4]
// 思路:每次下标和上标的数据对调,然后各自指针向中间移动一位,递归调用,直到上指标小于stack大小的一半结束
public static Stack<Integer> reverseStack(Stack<Integer> stack,int n){
if (stack != null && !stack.isEmpty()) {
int size = stack.size();
int bottomindex = size-n;
int topindex = n-1;
int bottomdata = stack.get(bottomindex);
int topdata = stack.get(topindex);
int temp = bottomdata;
bottomdata = topdata;
topdata = temp;
stack.set(bottomindex, bottomdata);
stack.set(topindex, topdata);
n--;
if (n>(size/2)) {
reverseStack(stack, n);
}
}
return stack;
}
3、双栈排序练习题
请编写一个程序,按升序对栈进行排序(即最大元素位于栈顶),要求最多只能使用一个额外的栈存放临时数据,但不得将元素复制到别的数据结构中。
给定一个int[] numbers(C++中为vector<int>),其中第一个元素为栈顶,请返回排序后的栈。请注意这是一个栈,意味着排序过程中你只能访问到第一个元素。
测试样例:
[1,2,3,4,5]
返回:[5,4,3,2,1]
public class TwoStacks {
public ArrayList<Integer> twoStacksSort(int[] numbers) {
// write code here
int len = numbers.length;
int[] help = new int[len];
int n = len - 1;
int m = -1;
while(n >= 0){
int key = numbers[n--];
if(m == -1){
help[++m] = key;
}else{
if(help[m] > key){
help[++m] = key;
}else{
int k = m;
while(k>=0 && help[k]<=key){
help[k+1] = help[k];
k --;
}
help[k+1] = key;
m++;
}
}
}
ArrayList<Integer> list = new ArrayList<Integer>();
for(int i = 0; i < help.length; i++){
list.add(help[i]);
}
return list;
}
}