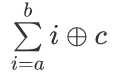2020.10.31
题目描述
求异或和 \(1\leq a,b\leq 2^{63}-1\),答案对 23333333333333333 (质数)取模
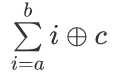
解法
先转换为前缀做差,设 \(f(x)\) 表示 \([0,x]\) 的数的异或和。答案就是 \(f(b)-f(a-1)\)
因为是异或,不同位间不会产生影响,所以考虑把每一位分开算贡献。若 \(c\) 的第 \(i\) 位是 \(v_i\),那么贡献就是 \(a\) 到 \(b\) 的所有数中第 \(i\) 位是 \(v_i\ xor \ 1\) 的数的出现次数乘上 \(1<<i\) 。
求 \(f(x)\)。记 \(ned=v_i \ xor \ 1\),\(lim\) 表示 \(x\) 的第 \(i\) 位是多少,则 \(lim=(x>>i)\&1\)。可以分三种情况快速求出每一位需要的值的个数:
- \(ned=lim\)。那么此时第 \(i\) 位取到上限,若第 \(i\) 位之前的都取到上界(1种),则后面的数都不能超过上界,贡献为后面的数个个数加一(有0),即 \(x-((x>>i)<<i)+1\),总的贡献为 \((x-((x>>i)<<i)+1)\times(1<<i)\)
- \(ned=1,lim=0\)。若前面取到上界,那么当前为就取不到 \(1\),那么前面一定不能取上界,因此后面的数就可以随便取。前面的贡献是 \((x>>(i+1))\),后面的贡献是 \(1<<i\) ,根据乘法原理总的贡献是 \((x>>(i+1))\times(1<<i)\times(1<<i)\)
- \(ned=0,lim=1\)。前面的只要不超过上界就行了,贡献为 \((x>>(i+1))+1\) (有0),因为第 \(i\) 位要取 \(0\),就没有达到上界,后面的可以随便取。总的贡献为 \(((x>>(i+1))+1)\times(1<<i)\times(1<<i)\)。
Tips
疑惑核
原文:https://www.cnblogs.com/wwlwQWQ/p/13912851.html