有一个初始全白的\(n*m\)大小的二维网格,每次可以选择一行或一列染全白或全黑。问可以通过任意次该操作得到多少不同的网格。答案对998244353取模。
不难发现,无论怎么染色,都不可能得到这样的方案,使得
形象的理解一下:
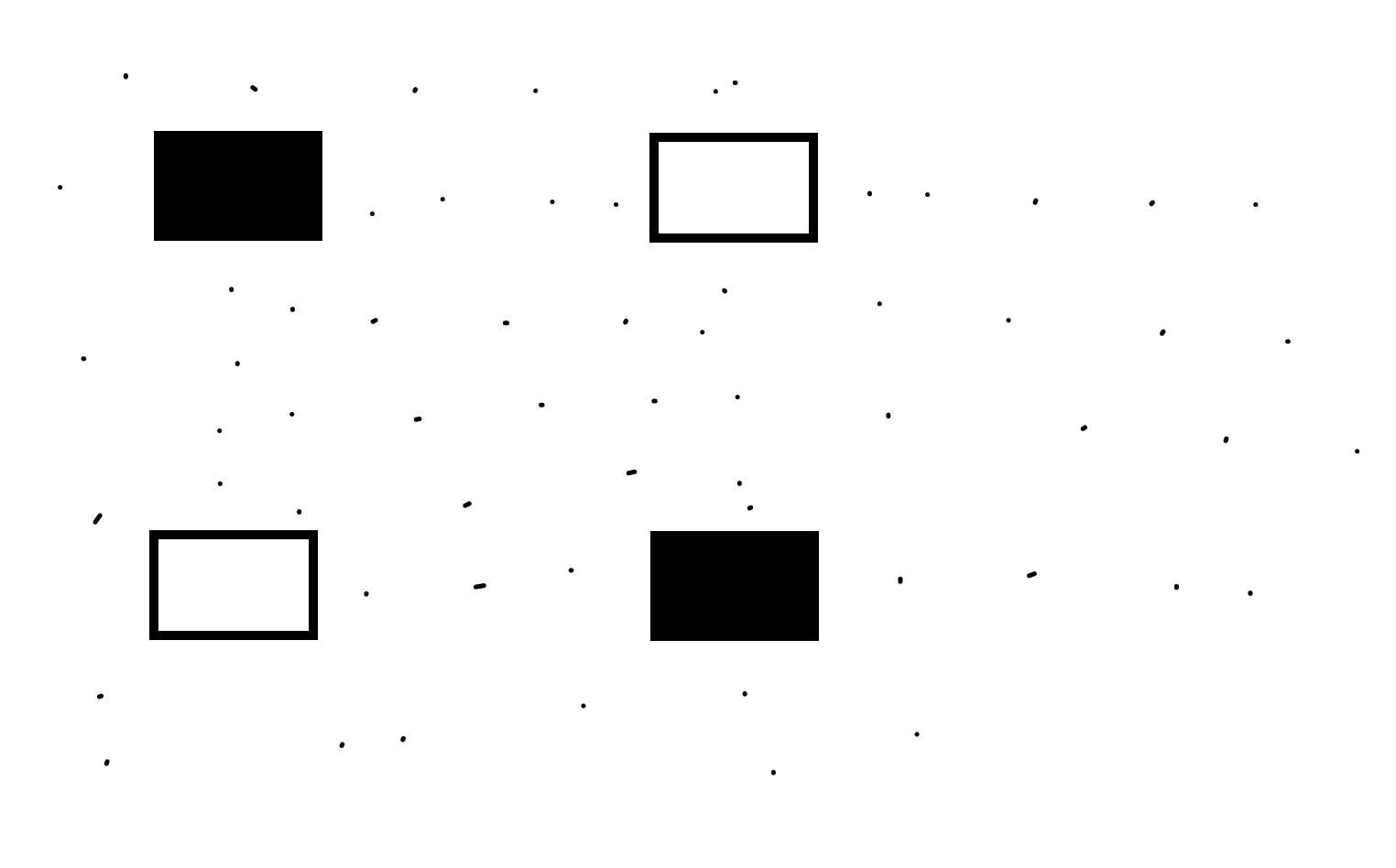
原理就是在染色的时候是同一行/列染色的,绝对不可能构成这种(可以手推一下,这个很显然)
接下来就是求有多少种。
不难发现,不同种但是颜色数量相同的网格是可以通过平移一行/列得到的,那么我们可以通过平移,将原本乱七八糟的网格变换成这样:

发现这个图形是可以正着构造的。
但是对于每一个形状如何计算有多少种可能呢?套用斯特林数即可。
当然,\(O(n^2)\)是过不去的,使用信仰\(FFT\)即可\(100pts\)
什么?Where is code?
我信仰还不足,不会写\(FFT\)
【待更新】
原文:https://www.cnblogs.com/send-off-a-friend/p/13929148.html