本章节实现的算法功能主要借鉴参考于
微信公众号:裸睡的猪
微信号:IT--Pig
感兴趣的朋友可以关注...(我也是他的小粉丝...)
首先用一张图了解下各排序方法的时间复杂度、空间复杂度及其稳定性:
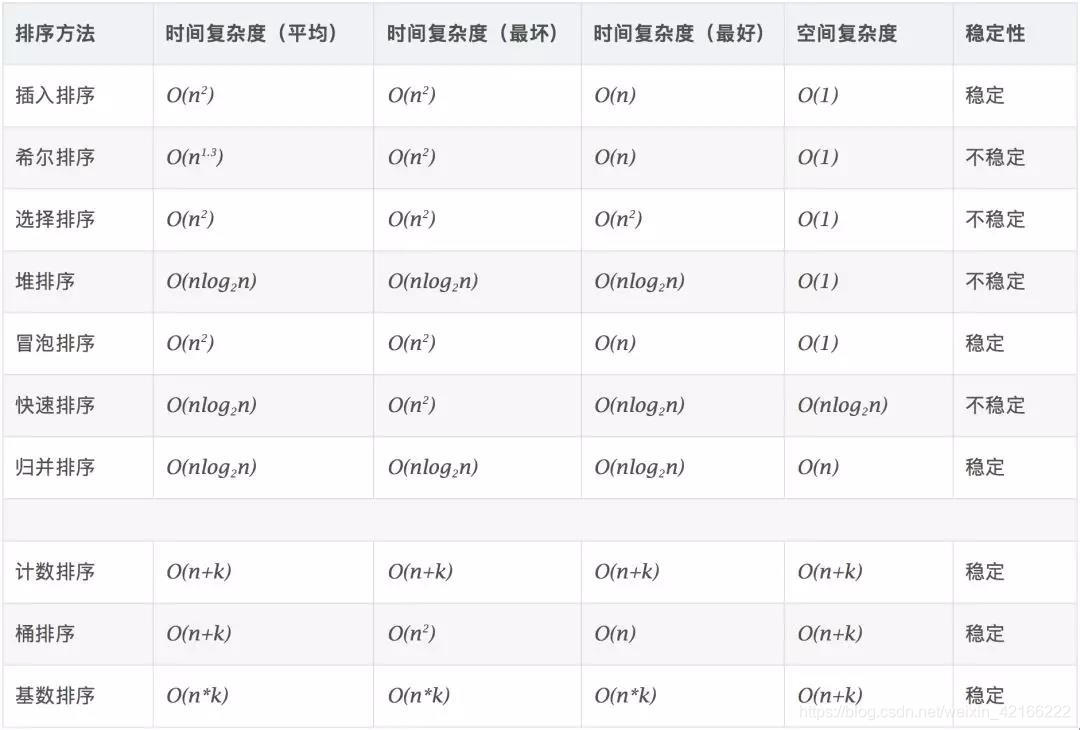
冒泡排序(Bubble Sort)的原理是通过依次比较两个相邻的元素,将较大的值向后移动,最终完成排序。

def bubble_sort(arr):
"""冒泡排序"""
# 第一层表示循环层数
for i in range(len(arr) - 1):
# 第二层表示具体比较那两个元素
for j in range(len(arr) - 1 - i):
if arr[j] > arr[j + 1]:
# 如果前面的大于后面的,则交换位置
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr
选择排序(Selection sort)的原理是每一次从需要排序的数据中选出最小或最大的元素,并将它放在序列的第一个位置。

def selection_sort(arr):
"""选择排序"""
# 第一层表示循环的次数
for i in range(len(arr) - 1):
# 将起始元素设为最小值
min_index = i
# 第二层表示最小元素和后面的元素逐个比较
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_index]:
# 如果当前元素比最小值小,则把当前元素下标设置为最小值下标
min_index = j
# 查找一遍后,将最小值与初始元素交换位置
arr[min_index], arr[i] = arr[i], arr[min_index]
return arr
插入排序(Insertion-Sort)原理是构建有序序列,对于未排序的序列,在已排好的序列中从后向前扫描,找到相应位置并插入,以此完成排序。

def insertion_sort(arr):
"""插入排序"""
# 第一层表示循环插入的次数
for i in range(1, len(arr)):
# 设置当前需要插入的元素
element = arr[i]
# 与当前元素进行比较的比较元素
pre_index = i - 1
while pre_index >= 0 and arr[pre_index] > element:
# 当比较元素大于当前元素,交换位置,后移比较元素
arr[pre_index + 1] = arr[pre_index]
# 向前选择下一个比较元素
pre_index -= 1
# 当比较元素小于当前元素,则将当前元素插在其后面
arr[pre_index + 1] = element
return arr
希尔排序(Shell’s Sort)是插入排序的一种,是直接插入排序算法的一种更高效的改进版本,它与插入排序的不同之处在于,它会优先比较距离较远的元素。
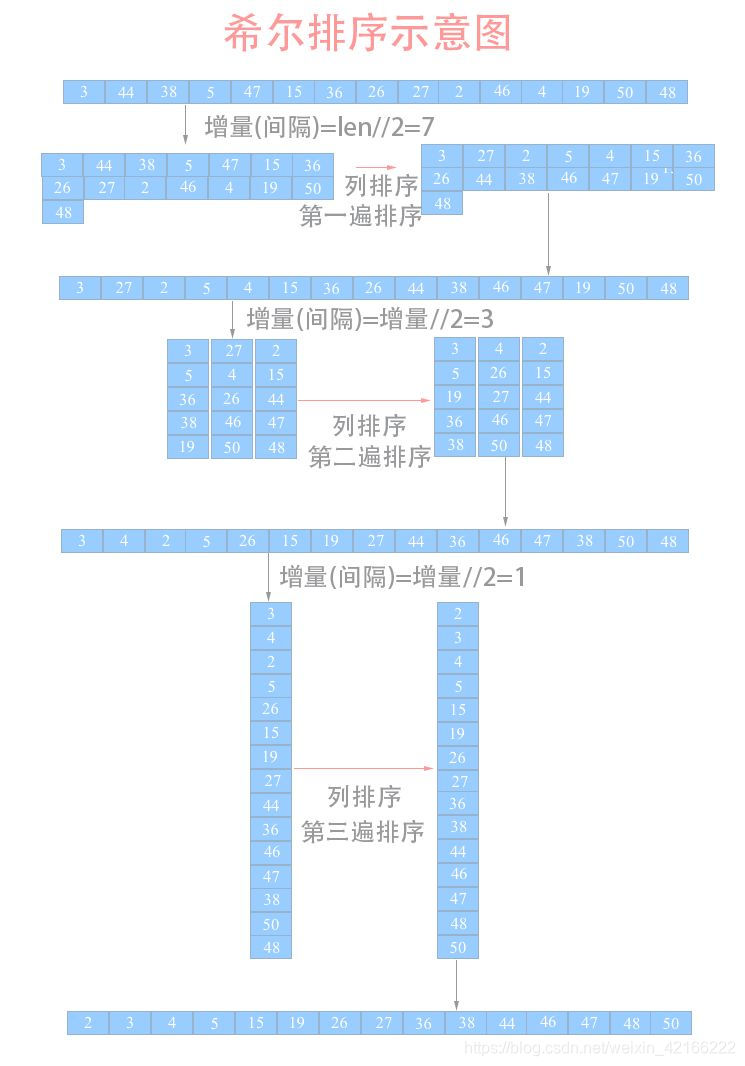
已知的最增量式是由 Sedgewick 提出的 (1, 5, 19, 41, 109,…), 该步长的项来自 9 4^i - 9 2^i +1 和 4^i - 3 2^i + 1
这两个算式。这项研究也表明比较在希尔排序中是最主要的操作,而不是交换。 用这样增量式的希尔排序比插入排序和堆排序都要快,甚至在小数组中比快速排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。
def shell_sort(arr):
"""希尔排序"""
# 取整计算增量(间隔)值
gap = len(arr) // 2
while gap > 0:
# 从增量值开始遍历比较
for i in range(gap, len(arr)):
j = i
element = arr[i]
# 元素与其他同列的前面每个元素比较,如果比前面小则互换
while j - gap > 0 and element < arr[j - gap]:
arr[j] = arr[j - gap]
arr[j - gap] = element
# j -= gap
# arr[j] = element
# 缩小增量(间隔)值
gap //= 2
return arr
归并排序(MERGE-SORT)主要采用分治法(Divide and Conquer),归并排序适用于子序列有序的数据排序。
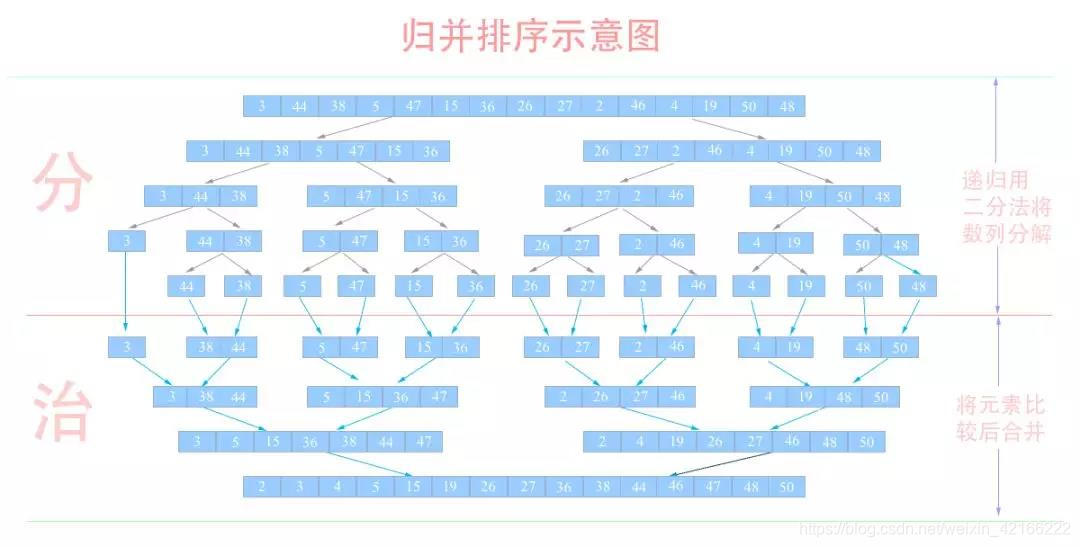
分治法(Divide-and-Conquer):将原问题划分成 n 个规模较小而结构与原问题相似的子问题;递归地解决这些问题,然后再合并其结果,就得到原问题的解。
def merge_sort(arr):
"""归并排序"""
if len(arr) == 1:
return arr
# 使用二分法将数列分为两个
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
# 使用递归运算
return marge(merge_sort(left), merge_sort(right))
def marge(left, right):
"""排序合并两个数列"""
result = []
# 两个数列都有值
while len(left) > 0 and len(right) > 0:
# 左右两个数列第一个最小放前面
if left[0] < right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
# 只有一个数列中还有值,直接添加
result += left
result += right
return result
快排的实现方式多种多样,最简单易懂的是分治+迭代
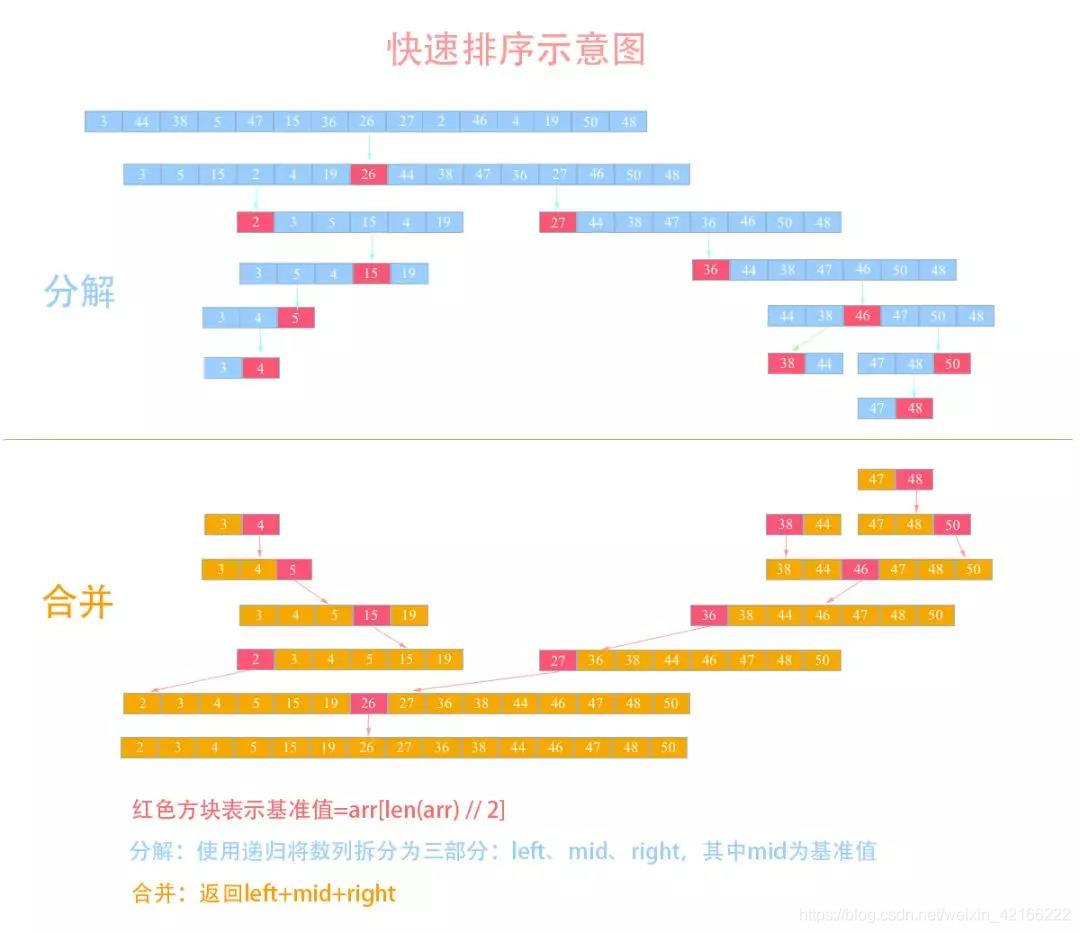
一行代码实现快排:
quick_sort = lambda array: array if len(array) <= 1 else quick_sort([item for item in array[1:] if item <= array[0]]) + [array[0]] + quick_sort([item for item in array[1:] if item > array[0]])
举个例子,假设我现在有一个数列需要使用快排来排序:{3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48},我们来看看使用快排的详细步骤:
def quick_sort(arr):
"""快速排序"""
if len(arr) < 2:
return arr
# 选取基准,任意挑选,这里选择中间的数
mid = arr[len(arr) // 2]
# 定义基准左右两侧数列
left, right = [], []
# 从原始数据中移除基准数值
arr.remove(mid)
for element in arr:
# 大于等于基准值放右边,小于放左边
if element >= mid:
right.append(element)
else:
left.append(element)
# 采用迭代的方式进行比较
return quick_sort(left) + [mid] + quick_sort(right)
最后大家如果感兴趣,想了解具体文章、代码和各个排序算法的性能比较可以关注
微信公众号:裸睡的猪
他的公众号文章链接:排序汇总
也可以移步我的GitHub
MangoloD
原文:https://www.cnblogs.com/Mango1106/p/13950153.html