岭回归如何解决共线性问题
为什么会有岭回归?
- 解决一元线性或多元线性回归的共线性问题
- 实际上是针对线性回归算法局限性的?个改进类算法,优化?的是要解决系数矩阵X_T*X不可逆的问题(X_T为矩阵X的转置矩阵)
岭回归怎么解决共线性问题?
- 第一步:岭回归的损失函数的完整表达式:
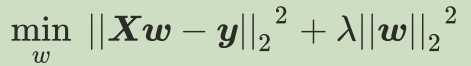
损失函数解释:
- 在多元线性回归的损失函数上加上了正则项,表达为系数w的L2范式(即w的平方项)乘以正则化系数λ
-
第二步:使用最小二乘法求解,可得: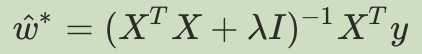
此时只要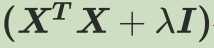 存在逆矩阵,就可以解出w
存在逆矩阵,就可以解出w
-
第三步:这时如果原本的特征矩阵中存在共线性,则我们的方阵就会不满秩,即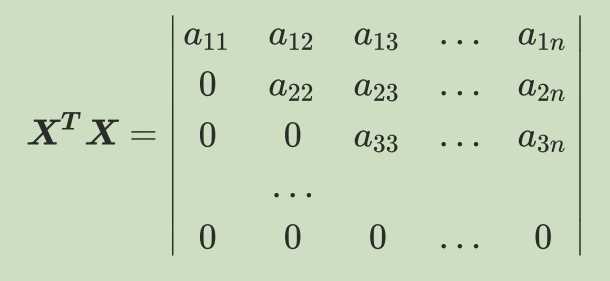
此时方阵不可逆,最小二乘法也就无法使用得到最佳的参数
-
第四步:然而如果这时加上λI之后:
这时不存在全0行或者全零列,除非:
- λ等于零
- 原本的矩阵中存在对角线上元素为-λ, 其他元素都为0的行或列
否则矩阵永远满秩,故解决了共线性问题
【岭回归作用总结】
- 使得矩阵最终运算结果满秩,即降低了原数据集特征列的共线性影响
- 相当于对所有的特征列的因变量解释程度进?了惩罚,且λ越?惩罚作?越强
回归分析-解析岭回归解决的共线性问题
原文:https://www.cnblogs.com/oten/p/13953220.html
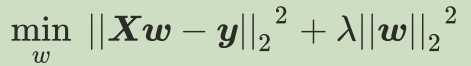
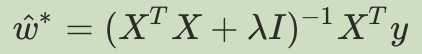
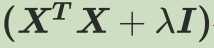 存在逆矩阵,就可以解出w
存在逆矩阵,就可以解出w
