1.流程
2个子序列,直到不能再分割。(序列中只剩1个元素)2个子序列合并成一个有序序列,直到最终只剩下1个有序序列。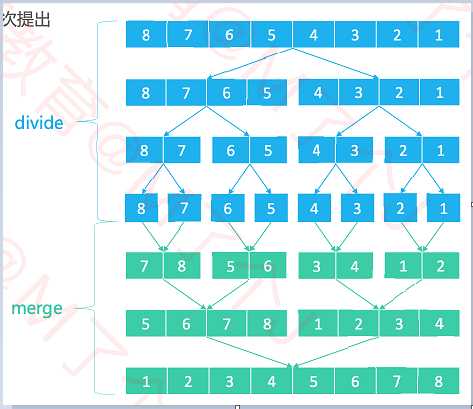
2. divide(划分)
public class MergeSort<T extends Comparable<T>> extends Sort<T> {
// 准备一段临时的数组空间 再merge时使用
private T[] leftArray;
/**
* 对 [begin, end) 范围的数据进行归并排序
*/
private void sort(int begin, int end) {
if (end - begin < 2) return;
int mid = (begin + end) >> 1;
sort(begin, mid);
sort(mid, end);
// 合并操作
merge(begin, mid, end);
}
}
3. merge(合并)
? 流程:
头节点的指针(li , ri)。黑色代表已填入的数据,黄色代表这一轮比较较小的值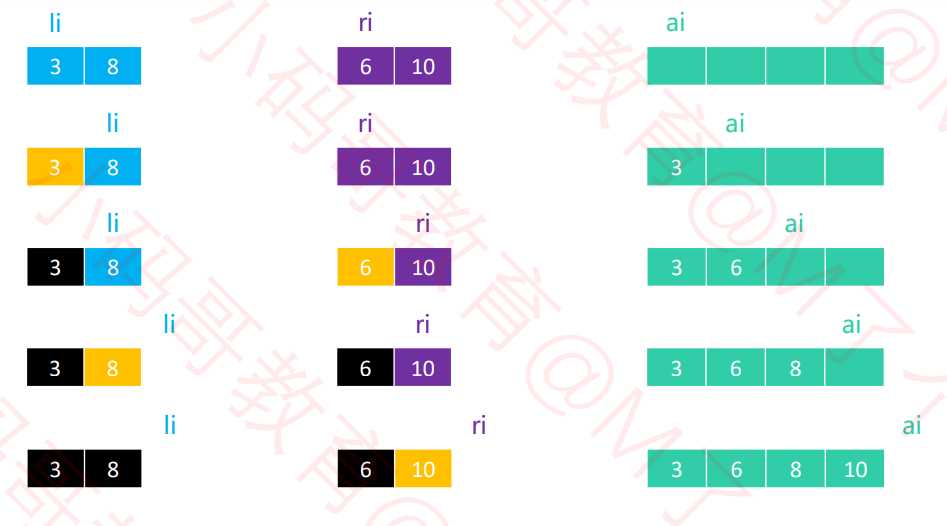
? 细节

3和8比较的结果放入数组左侧,那么8的值就会被覆盖merge操作。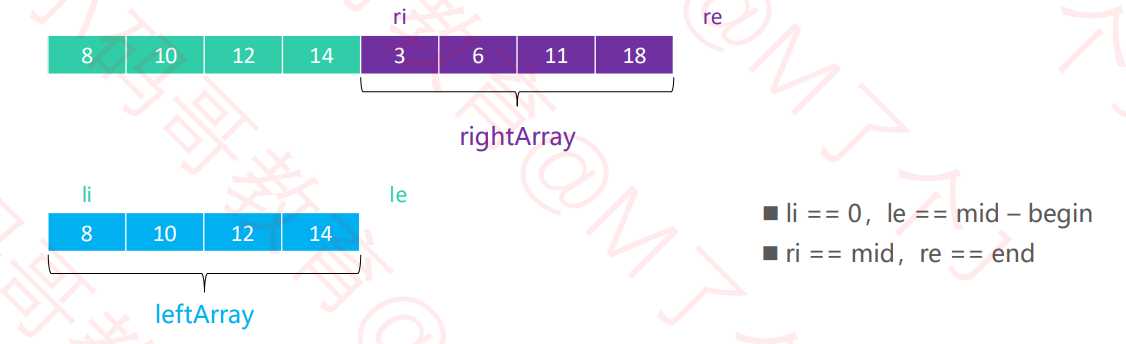
? 实例:
黑色代表已填入的数据,黄色代表这一轮比较较小的值。粉红色代表该位置已经排好序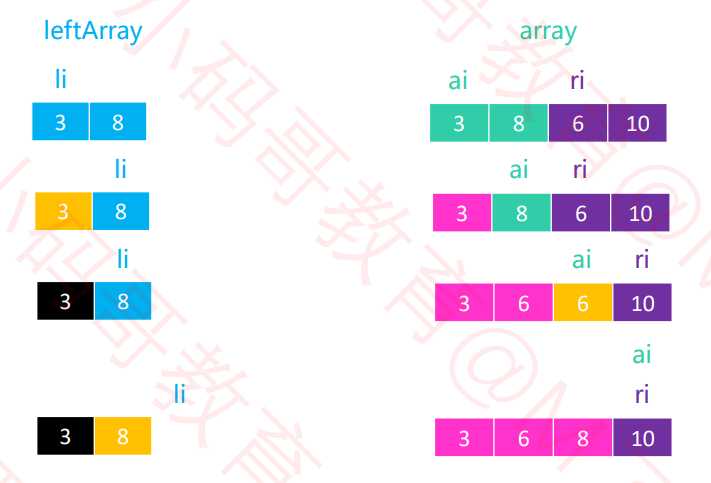
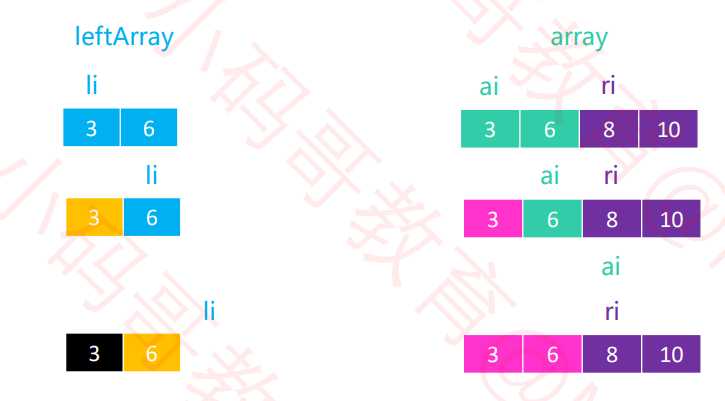
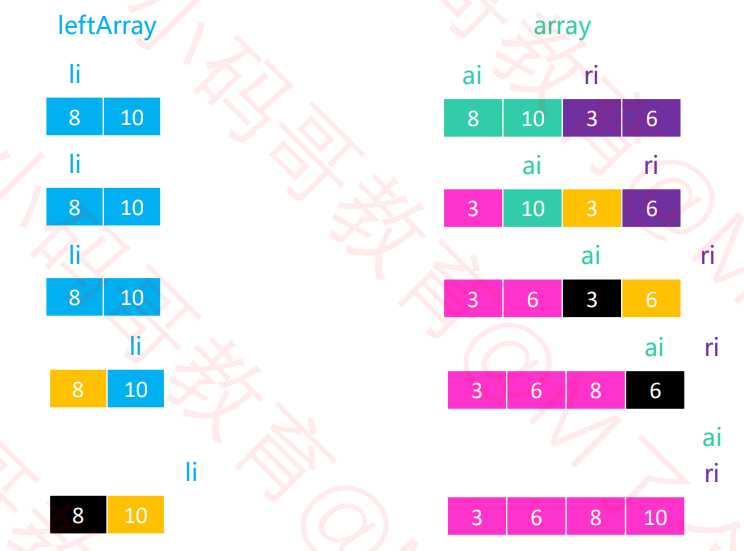
代码实现:
public class MergeSort<T extends Comparable<T>> extends Sort<T> {
private T[] leftArray;
@Override
protected void sort() {
// 临时数组 用来归并时记录左边数组的元素
leftArray = (T[]) new Comparable[array.length >> 1];
sort(0, array.length);
}
//不断地将当前序列平均分割成2个子序列
//直到不能再分割(序列中只剩1个元素)
// [begin, mid) [mid, end) 左闭右开
private void sort(int begin, int end) { //递归将元素分割
//至少要有两个元素 一个元素无法再分
if (end - begin < 2) return;
int mid = (end + begin) >> 1;
sort(begin, mid);
sort(mid, end);
//将两个子序列合并
merge(begin, mid, end);
}
private void merge(int begin, int mid, int end) {
int li = 0, le = mid - begin;
int ri = mid, re = end;
int ai = begin;
// 复制左边的数组
for (int i = li; i < le; i++) {
leftArray[i] = array[i + begin];
}
// 当左边未结束时
while (li < le) {
// 当右边未结束且右边的元素较小时
if (ri < re && cmp(leftArray[li], array[ri]) > 0) {
array[ai++] = array[ri++];
} else { // 左边的元素小于等于右边
array[ai++] = leftArray[li++];
}
}
}
}
O(nlogn),属于稳定排序。O(n)。? 复杂度分析
? 归并排序花费的时间
T (n) = 2 ? T (n/2) + O(n)
T (1) = O(1)
T (\(n/n\)) = T (n/2) / (n/2) + O(1)
? 令 S (n) = T (n /n)
S (1) = O(1)
S (n) = S (n/2) + O(1) = S (n/4) + O(2) = S (n/8) + O(3) = S (n / 2^k^) + O(k) = S (1) + O(\(logn\)) = O(\(logn\))
T (n) = n ? S n = O(\(nlogn\))
1 . 快速排序 – 执行流程
① 从序列中选择一个轴点元素(pivot) 假设每次选择 0 位置的元素为轴点元素
? 
② 利用 pivot 将序列分割成 2 个子序列
? ? 将小于 pivot 的元素放在pivot前面(左侧)
? ? 将大于 pivot 的元素放在pivot后面(右侧)
? ? 等于pivot的元素放哪边都可以

③ 对子序列进行 ① ② 操作
? ? 直到不能再分割(子序列中只剩下1个元素)
2 . 快速排序 – 轴点构造
6作为轴点,备份一份。
右边(end)开始扫描数组。7,大于6a,执行end--即可5,小于6a,用5覆盖6a的位置,begin++。
左边(begin)继续扫描。8a,大于6a,用8a覆盖5的位置,end--。
右边(end)继续扫描9,大于6a,执行end--,不做其他操作。
4,小于6a,用4覆盖8a的位置,begin++。
8b,大于6a,用8b覆盖4的位置,end--。
6b,等于6a,用6b覆盖8b的位置,begin++。
2,小于6a,begin++。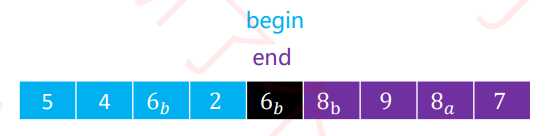
begin和end重叠,则轴点构造完成。将备份的6a,覆盖6b的位置。
3 . 代码实现
public class QuickSort<T extends Comparable<T>> extends Sort<T> {
@Override
protected void sort() {
sort(0, array.length);
}
/**
* 对 [begin, end) 范围的元素进行快速排序
*/
private void sort(int begin, int end) {
if (end - begin < 2) return; //至少有两个元素才执行快速排序
// 确定轴点位置 O(n),并进行一次快速排序
int mid = pivotIndex(begin, end);
// 对子序列进行快速排序
sort(begin, mid);
sort(mid + 1, end);
}
/**
* 构造出 [begin, end) 范围的轴点元素,并进行一次快速排序
* @return 轴点元素的最终位置
*/
private int pivotIndex(int begin, int end) {
// 为了降低最坏情况(O(n^2)的时间复杂度)的出现概率,随机选择一个元素跟begin位置进行交换
swap(begin, begin + (int)(Math.random() * (end - begin)));
// 备份begin位置的元素
T pivot = array[begin];
// end指向最后一个元素
end--;
// 如果begin == end 则退出排序
while (begin < end) {
while (begin < end) {
if (cmp(pivot, array[end]) < 0) { // 右边元素 > 轴点元素
end--; // 只位移,不进行元素交换
} else { // 右边元素 <= 轴点元素
array[begin++] = array[end];
break; //执行完一次操作后,需要掉头,所以执行一个break
// 此处 右边元素等于轴点元素时 依旧交换 是为了使左右分布更加均匀 避免最坏的情况
}
}
while (begin < end) {
if (cmp(pivot, array[begin]) > 0) { // 左边元素 < 轴点元素
begin++;
} else { // 左边元素 >= 轴点元素
array[end--] = array[begin];
break; // 通过两个break,能实现两个while交替执行。
}
}
}
// 将轴点元素放入最终的位置
array[begin] = pivot;
// 返回轴点元素的位置
return begin;
}
}
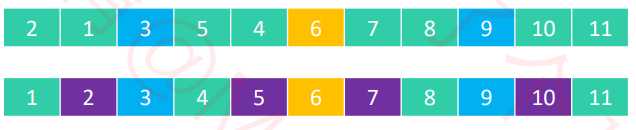
4 . 快速排序 – 与轴点相等的元素
元素a与轴点元素相等,则会将轴点元素与元素a替换位置。利用目前的算法实现,轴点元素可以将序列分割成 2 个均匀的子序列。
元素a与轴点元素相等时,不进行替换,那么最终得到的数组会非常不平衡(黄色轴点在数组中的位置 会将数组分成两个极度不均匀的两个子序列),导致出现最坏时间复杂度O(n^2)。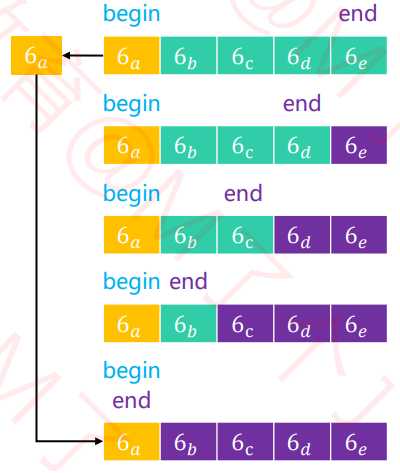
5 . 时间复杂度
T(n) = 2 ? T(n/2) + O (n) = O(nlogn)。T(n) = T(n ? 1) + O n = O(n^2)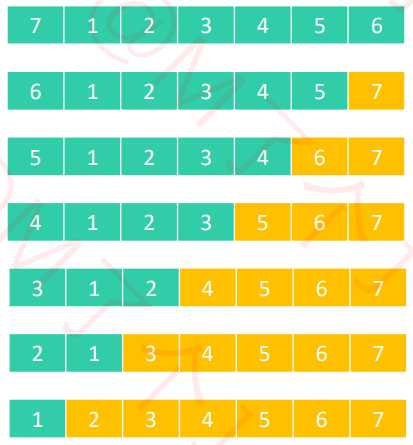
随机选择轴点元素。O(logn)。不稳定排序。1 . 概念
希尔排序把序列看作一个矩阵,分为m列,逐列进行排序。
m从某个整数逐渐减为1,当m为1时,整个序列将完全有序。因此也被称为递减增量排序。
矩阵的列数取决于步长序列,如果步长序列为【1,5,19,41,109...】就代表依次分为109列,41列,19列,5列,1列进行排序。不同的步长序列,执行效率也不同。
2 . 执行流程
n/2^k(k 取1 2 3 4 ...),比如n为16,步长序列是【1,2,4,8】
8列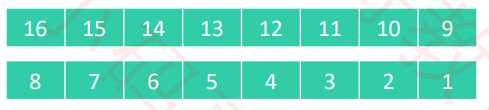
8列按列进行排序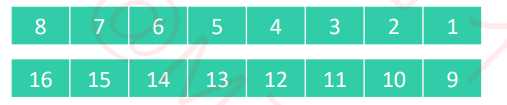

4列进行排序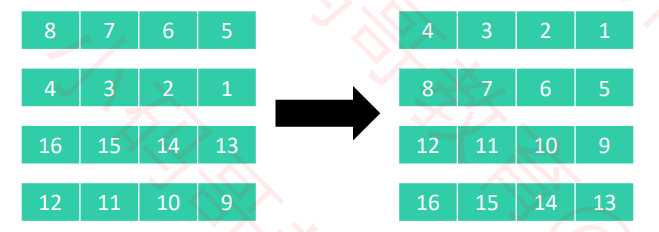

2列进行排序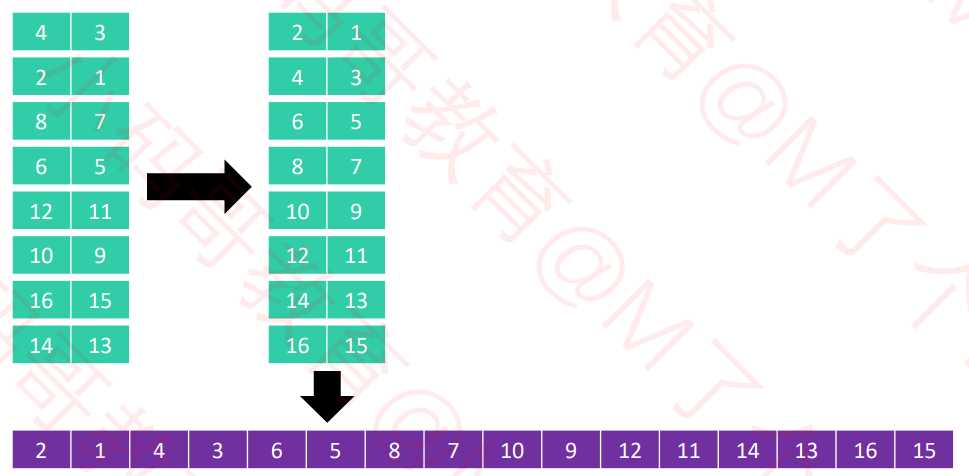
1列进行排序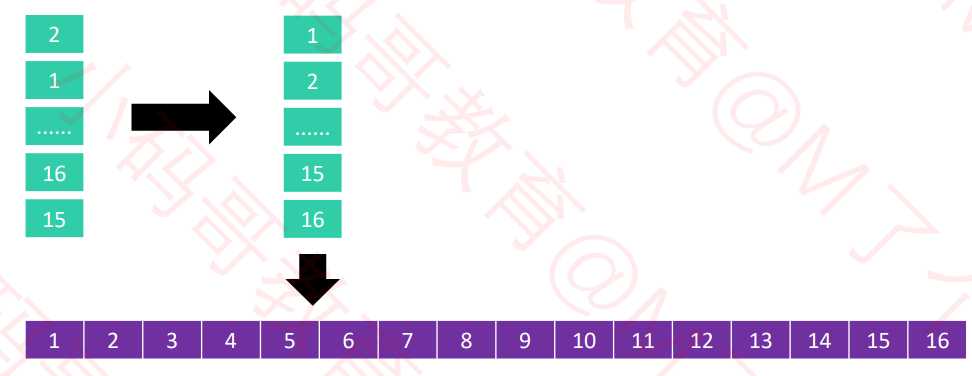
8列变为1列的过程中,逆序对的数量在逐渐减少。3 . 实例
11个元素,步长序列是【1,2,5】。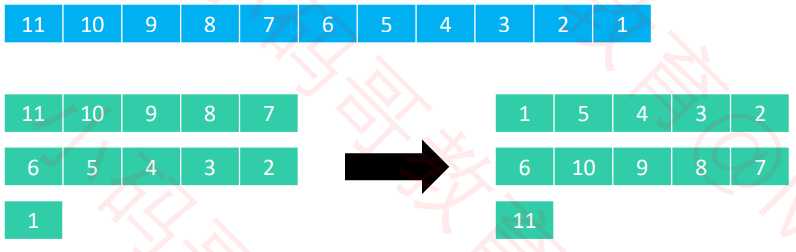
假设元素在第 col 列、第 row 行,步长(总列数)是 step
那么这个元素在数组中的索引是 col + row * step
比如 9 在排序前是第 2 列、第 0 行,那么它排序前的索引是 2 + 0 * 5 = 2
比如 4 在排序前是第 2 列、第 1 行,那么它排序前的索引是 2 + 1 * 5 = 7
4 . 代码实现
@Override
protected void sort() {
// 获取步长序列
List<Integer> stepSequence = shellStepSequence();
for (Integer step : stepSequence) {
//按步长序列依次排序 使用插入排序
sort(step);
}
}
// 按照希尔本人给出的n/2^k 求出步长序列
//希尔本人给出的步长序列,最坏情况时间复杂度是O(n^2)
private List<Integer> shellStepSequence() {
List<Integer> stepSequence = new ArrayList<>();
int step = array.length;
while ((step >>= 1) > 0) {
stepSequence.add(step);
}
return stepSequence;
}
/**
* 分成step列进行排序
*/
private void sort(int step) {
// 一共有多少列,就排多少次
// col : 第几列,column的简称
for (int col = 0; col < step; col++) { // 对第col列进行排序
// 每一列元素的索引为:col、col+step、col+2*step、col+3*step
// 插入排序
for (int begin = col + step; begin < array.length; begin += step) {
int cur = begin;
while (cur > col && cmp(cur, cur - step) < 0) {
swap(cur, cur - step);
cur -= step;
}
}
}
}
5 . 最好的步长序列
最好的步长序列,最坏情况时间复杂度是O(n^4/3)。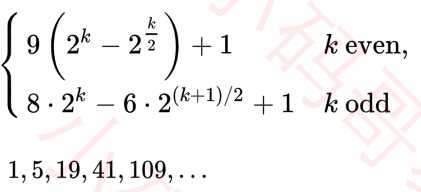
代码实现
private List<Integer> sedgewickStepSequence() {
List<Integer> stepSequence = new LinkedList<>();
//k从0开始
int k = 0, step = 0;
while (true) {
if (k % 2 == 0) {
int pow = (int) Math.pow(2, k >> 1);
step = 1 + 9 * (pow * pow - pow);
} else {
int pow1 = (int) Math.pow(2, (k - 1) >> 1);
int pow2 = (int) Math.pow(2, (k + 1) >> 1);
step = 1 + 8 * pow1 * pow2 - 6 * pow2;
}
if (step >= array.length) break;
stepSequence.add(0, step);
k++;
}
return stepSequence;
}
6 . 记录一次失败的尝试
利用二分法对希尔排序内部的插入排序再次进行优化
代码实现:
public class ShellSort1<T extends Comparable<T>> extends Sort<T> {
@Override
protected void sort() {
// 获取步长序列
List<Integer> stepSequence = shellStepSequence();
for (Integer step : stepSequence) {
//按步长序列依次排序 使用插入排序
sort(step);
}
}
// 根据 n/2^k 获取步长序列 最差为O(n^2)
private List<Integer> shellStepSequence() {
List<Integer> stepSequence = new ArrayList<>();
int step = array.length;
while ((step >>= 1) > 0) {
stepSequence.add(step);
}
return stepSequence;
}
private void sort(int setp) {
// 数组按步长分成setp列 对每列进行排序(减少逆序对)
for (int col = 0; col < setp; col++) {
for (int begin = col + setp; begin < array.length; begin += setp) {
insert(begin, search(col, begin, setp), setp);
}
}
}
//将元素插入到对应的位置
private void insert(int source, int dest, int step) {
T v = array[source];
for (int i = source; i > dest; i-= step) {
array[i] = array[i - step];
}
array[dest] = v;
}
/**
* 利用二分法找到元素对应的插入位置
* @param index 要插入的元素现在所在位置
*/
private int search(int col, int index, int step) {
T v = array[index];
int begin = col;
int end = index;
while (begin < end) {
// 求中间行
int beginRow = (begin - col) / step;
int endRow = (end - col) / step;
int midRow = (beginRow + endRow) >> 1;
int mid = col + midRow * step;
if (cmp(v, array[mid]) < 0) {
end = mid;
} else {
begin = mid + step;
}
}
return begin;
}
}
失败原因:
希尔排序分步长进行排序的目的是减少逆序对 从而减少内部插入排序的比较次数和交换次数(主要),而使用二分法优化 比较次数将与逆序对的数量无关,此时希尔排序最差会退化成用二分法优化的插入排序(甚至更差 因为比单纯插入排序多了比较次数(按步长多次排序) 但大部分情况下依旧比插入排序快,原因是减少了逆序对)
实际尝试过后 使用二分法再次优化在后续的按步长排序中比较次数相较于不使用越来越多 而交换次数基本未变
插入排序的比较次数主要取决于逆序对的个数, 而希尔排序开始分步长进行排序每一次都减少了逆序对的个数所以对下一个步长进行排序时 逆序对减少 相应的比较次数和交换次数也在减少, 尤其是当步长为1时 插入排序对每个元素比较和交换可以接近于O(1)级别 对整体排序可以达到O(n)级别。 所以希尔排序就是在不断地使下一次按步长排序接近O(n) 也就是接近有序,而使用二分法优化 对每个元素比较查找插入位置是O(logn) 实际排序复杂度为O(nlogn)
原文:https://www.cnblogs.com/coderlts/p/13964737.html