课本上所授的案例只说到了模26值时的加密方式,若要想模到任意模值,以256为例,考虑如何将其实现加密,解密,在此基础上再实现分组链接模式,即(CBC)。
首先来探讨算法,Hill密码的加密实现取决于一对可逆矩阵的变换。
核心公式为:
C=E(K,P)=PK mod 26;
P=D(K,C)=CK^-1 mod 26 =PKK^-1 =P;
可逆矩阵的性质满足于(K*K^-1) mod 26=E(单位矩阵,仅角平分线上值为1);
其模值换成256也是一样的,我们将键盘输入的明文用ASCII码来表示,查表可得ASCII正好有256位。第0个正好就是‘\0‘,为空值,键盘输入不得。将输入与其做差即可。
若分组时候,明文不能做到整除,课采用填充的方式,填入0即可,解密的时候只需删除即可得到原明文。
紧接着,我们来探讨可逆矩阵的求法,这对矩阵满足右式:(K*k^-1)%256=E;
我们用matlab软件来帮助实现。
矩阵求法如下:
为求出合适的矩阵K,在一个n*n阶矩阵中,任设二元素的值为x、y,其余元素给出具体的正整数数字,并令其行列式的值为+1或-1,可得一个二元一次或二元二次不定方程,可求其正整数解。如下例:
取K={{4 x 8 y},{12 1 6 9},{3 6 4 6},{2 11 3 8}};令|K|=1,得:-105x+187y=761,可借助matlab语言得其一正整数解:x=7,y=8;下面开始求其逆矩阵
K^-1:
设置为有理格式 : >>format rat
输入矩阵K的值: >>K=[4 7 8 8;12 1 6 9;3 6 4 6;2 11 3 8];
用 >>det(K) 命令验证矩阵K的行列式的值为1;
用 >>K1=inv(K)从数学角度求矩阵的逆K1
K1=[-112 -34 371 -128; -105 -32 348 -120; -39 -12 130 -45; 187 57 -620 214];
由于他的元素出现负整数,故将他的每一个元素加上256的若干倍,使他的元素全为正整数,再模256,
用>>K2=mod(K1+2560,256)命令得:
K2=[144 222 115 128; 151 224 92 136; 217 244 130 211; 187 57 148 214];
不难验证K*K2mod256=[1 0 0 0;0 1 0 0;0 0 1 0; 0 0 0 1];
故K2就是矩阵K的逆矩阵K^-1;
接下来K与K2用于加密解密过程即可。
在此我们采用分组链接的方式
分组链接:(CBC模式)在CBC模式中,后一组的密文都受前一组密文影响,第一组密文受初始向量IV影响,从而明文的重复排列不会反应在密文中。
假设e~k~()表示用密钥k进行的分组加密;e~k~^-1^()对应解密。 x~i~,y~i~表示长度为b的位字符串,IV表示长度为b的初始向量,(长度不够的字符串会按照指定的填充规则进行填充) 加密:y~1~=e~k~(x~1~ ⊕ IV) ? y~i~=e~k~(x~i~ ⊕ y~i-1~) ,i≥2 解密:x~1~=e~k~^-1^(y~1~)⊕ IV ? x~i~=e~k~^-1^(y~i~) ⊕ y~i-1~ ,i≥2
如果每次加密是都选择一个新的IV,则CBC模式就变成了一个概率加密方案,即相同的明文加密会生成不同的密文。
? 需要说明的是,如果每次选择IV的数值得当,则代换攻击会彻底失效,因为监听者无法识别加密的模式。但是如果若干次加密使用相同的IV,则监听者还是可以识别加密模式。
? 虽然(承接ECB的例子)这一次直接将我们的账户的密文替换上去已经不能实现向我们账户转账的效果,因为我们代换,会导致第四、五组消息都被破坏,但是有可能解密后,账户和金额仍然具有意义呢?(虽然可能性似乎很低)只是是随机的,不再可控了而已。但这仍然是银行所不可接受的。所以消息验证码和数字签名的作用显得尤为重要。
因为某些原因,使得某一组密文中出现了错误的bit,将影响这一组(整组)及其之后一组(相应位)分组的解密。由此产生了CBC反转字节攻击。另外与下面所讲的CFB模式一样,CBC模式也不能抵御重放攻击。
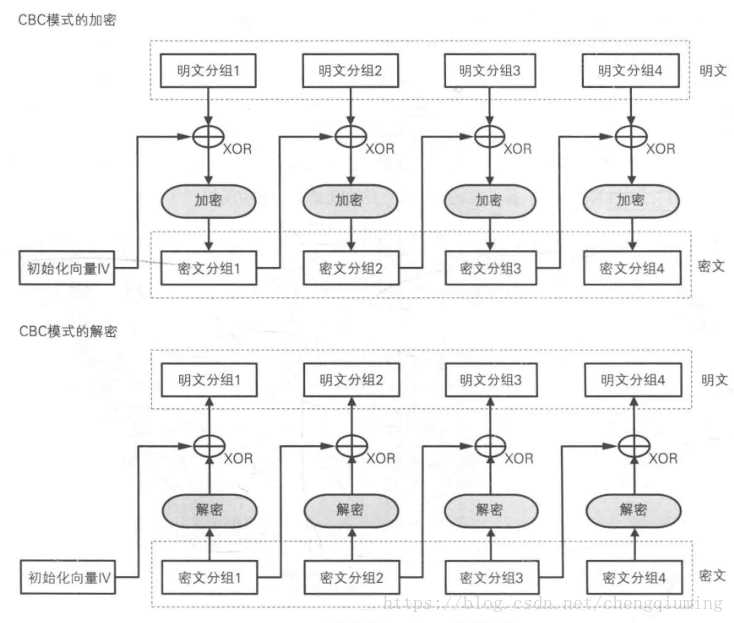
注意向量IV插入的位置,层层叠加,最终我们就实现了采用分组链接方式的Hillmod256算法,代码如下:
main.cpp:
#include <iostream> #include <string> #include "Hill.h" using namespace std; int main() { //cin >> str; string str = "paymoremoney"; vector<int> num1; for (int i = 0;i < str.size();i++) { num1.push_back(str[i] - ‘\0‘); } vector<int> num2 = Hencryption(num1); /*string str3 = ""; for (int i = 0;i < num2.size();i++) { str3 += ‘\0‘ + num2[i]; } cout << str3 << endl;*/ vector<int> num3 = Hdecryption(num2); string str2 = ""; for (int i = 0;i < num3.size();i++) { str2+= ‘\0‘ + num3[i]; } cout << str2 << endl; system("pause"); return 0; }
Hill.h:
#pragma once #include <iostream> #include <vector> using namespace std; vector<int> Hencryption(vector<int> num); vector<int> Hdecryption(vector<int> num);
Hill.cpp:
#include "Hill.h" vector<int> V = { 0,0,0,0 }; vector<int> Hencryption(vector<int> num) { vector<vector<int>> K = { {4,7,8,8},{12,1,6,9},{3,6,4,6},{2,11,3,8} }; vector<int> res; if (num.size() % 4 != 0) { int temp = num.size() % 4; switch (temp) { case 1: num.push_back(0); num.push_back(0); num.push_back(0); break; case 2: num.push_back(0); num.push_back(0); break; case 3: num.push_back(0); break; default: break; } } for (int i = 0;i < num.size() / 4;i++) { //进行分组链接加密 if (i == 0) { //异或 int a1 = V[0] ^ num[0]; int b1 = V[1] ^ num[1]; int c1 = V[2] ^ num[2]; int d1 = V[3] ^ num[3]; //加密 int a = a1 * K[0][0] + b1 * K[1][0] + c1 * K[2][0] + d1 * K[3][0]; int b = a1 * K[0][1] + b1 * K[1][1] + c1 * K[2][1] + d1 * K[3][1]; int c = a1 * K[0][2] + b1 * K[1][2] + c1 * K[2][2] + d1 * K[3][2]; int d = a1 * K[0][3] + b1 * K[1][3] + c1 * K[2][3] + d1 * K[3][3]; res.push_back(a % 256); res.push_back(b % 256); res.push_back(c % 256); res.push_back(d % 256); } else { num[i * 4 + 0] = res[(i - 1) * 4 + 0] ^ num[i * 4 + 0]; num[i * 4 + 1] = res[(i - 1) * 4 + 1] ^ num[i * 4 + 1]; num[i * 4 + 2] = res[(i - 1) * 4 + 2] ^ num[i * 4 + 2]; num[i * 4 + 3] = res[(i - 1) * 4 + 3] ^ num[i * 4 + 3]; //分组链接再加密,链接的是上一组的密文分组 int a = num[i * 4 + 0] * K[0][0] + num[i * 4 + 1] * K[1][0] + num[i * 4 + 2] * K[2][0] + num[i * 4 + 3] * K[3][0]; int b = num[i * 4 + 0] * K[0][1] + num[i * 4 + 1] * K[1][1] + num[i * 4 + 2] * K[2][1] + num[i * 4 + 3] * K[3][1]; int c = num[i * 4 + 0] * K[0][2] + num[i * 4 + 1] * K[1][2] + num[i * 4 + 2] * K[2][2] + num[i * 4 + 3] * K[3][2]; int d = num[i * 4 + 0] * K[0][3] + num[i * 4 + 1] * K[1][3] + num[i * 4 + 2] * K[2][3] + num[i * 4 + 3] * K[3][3]; res.push_back(a % 256); res.push_back(b % 256); res.push_back(c % 256); res.push_back(d % 256); } } //明文多出一两个怎么修改? return res; } vector<int> Hdecryption(vector<int> num) { vector<vector<int>> K = { { 144,222,115,128},{ 151,224,92,136 },{ 217,244,130,211 },{187,57,148,214} }; vector<int> res; for (int i = 0;i < num.size() / 4;i++) { int a = num[(i)* 4 + 0] * K[0][0] + num[(i)* 4 + 1] * K[1][0] + num[(i)* 4 + 2] * K[2][0] + num[(i)* 4 + 3] * K[3][0]; int b = num[(i)* 4 + 0] * K[0][1] + num[(i)* 4 + 1] * K[1][1] + num[(i)* 4 + 2] * K[2][1] + num[(i)* 4 + 3] * K[3][1]; int c = num[(i)* 4 + 0] * K[0][2] + num[(i)* 4 + 1] * K[1][2] + num[(i)* 4 + 2] * K[2][2] + num[(i)* 4 + 3] * K[3][2]; int d = num[(i)* 4 + 0] * K[0][3] + num[(i)* 4 + 1] * K[1][3] + num[(i)* 4 + 2] * K[2][3] + num[(i)* 4 + 3] * K[3][3]; res.push_back(a % 256); res.push_back(b % 256); res.push_back(c % 256); res.push_back(d % 256); } //到这里为止,相当于每一个密文分组都过了解密那一步,接下来是与本组的密文分组异或得到明文分组 //解密组存在于res中,密文在num中,res此时是解密分组,不是最终的明文分组 for (int i = 0;i < num.size() / 4;i++) { if (i == 0) { res[0] = V[0] ^ res[0]; res[1] = V[1] ^ res[1]; res[2] = V[2] ^ res[2]; res[3] = V[3] ^ res[3]; } else { res[i * 4 + 0] = num[(i - 1) * 4 + 0] ^ res[i * 4 + 0]; res[i * 4 + 1] = num[(i - 1) * 4 + 1] ^ res[i * 4 + 1]; res[i * 4 + 2] = num[(i - 1) * 4 + 2] ^ res[i * 4 + 2]; res[i * 4 + 3] = num[(i - 1) * 4 + 3] ^ res[i * 4 + 3]; } } int j = res.size() - 1; while (res[j] == 0) { res.pop_back(); j--; } return res; }
原文:https://www.cnblogs.com/awangkuo/p/13966946.html