转自:https://blog.csdn.net/dark_scope/article/details/8880547
转自:离散数学(第五版)耿素云 屈婉玲 张立昂 编著
一,概述
定义:若能将无向图 G = <V , E> 的顶点集 V 划分成两个不相交的非空子集 V1 和 V2,使得 G 中任何一条边的两个端点一个属于 V1,另一个属于 V2,则称 G 为 二部图。
定义:设 G = <V , E> 为无向图,M 是 E的子集,若 M 中任意两条边均不相邻,则称 M 为 G 中的 匹配。若在 M 中再加入任何一条边就都不是匹配了,则称 M 为 极大匹配,边数最多的匹配称为 最大匹配,最大匹配中边的条数称为 G 的 匹配数。显然,最大匹配是极大匹配,但反之不一定成立。
匈牙利算法:大概就是求二部图的最大匹配的匹配数,其算法核心是:寻找增广路径
二,举例
假设现有 m个男生,n个女生,每个人都可能对多名异性有好感,如果一对男女互有好感,那么你就可以把这一对撮合在一起,你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
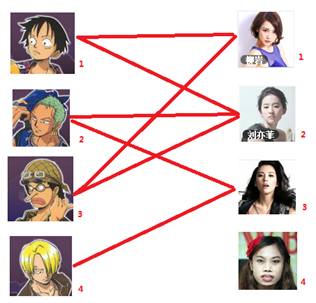
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
(注:本例子三观毁人,纯属为了容易理解,不包含本人观点,大家千万别较真。)
===============================================================================
总体上,你只需遍历一遍男生就可以完成该算法。
===============================================================================
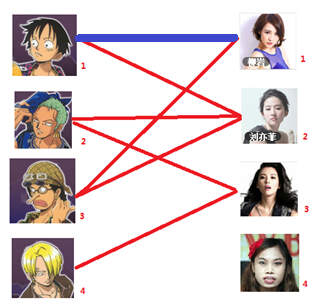
遍历到第一个男生 : 先试着给他找妹子,发现第一个和他相看两不厌的女生(1号女生) 还名花无主,于是将两人连上一条蓝线,表示 两人成为情侣。
===============================================================================
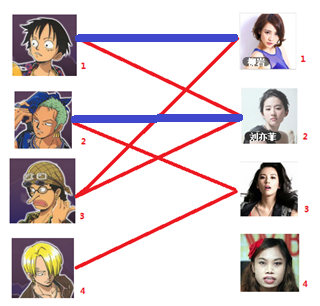
遍历到第二个男生:还是尝试着给他找妹子,发现第一个和他相看两不厌的女生(2号女生) 名花无主,于是将两人连上一条蓝线,表示 两人成为情侣。
===============================================================================
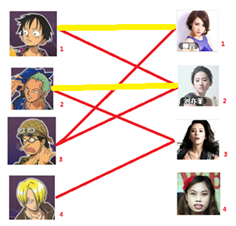
遍历到第三个男生:还是尝试着给他找妹子,发现第一个和他相看两不厌的女生(1号女生) 已经有主了,这时候这个第三个男生就直接暴走了,决定和第一个男生抢 1号女生的配偶权。第一个男生抢不过。于是此时男女生关系如图:(黄色表示这条边被临时拆掉)
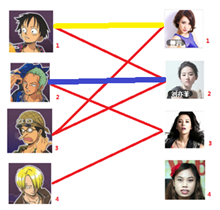
气急败坏的第二个男生决定去找第二个和他相看两不厌的女生(2号女生) ,结果发现她现在 2号女生 已经名花有主了,这时候这个第一个男生就直接暴走了,决定和第二个男生抢 2号女生 的配偶权。第二个男生抢不过。于是此时男女生关系如图:(黄色表示这条边被临时拆掉)
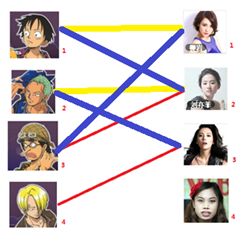
气急败坏的第三个男生决定去找第二个和他相看两不厌的女生(3号女生) ,结果发现她现在 2号女生 名花无主,于是将两人连上一条蓝线,表示 两人成为情侣。
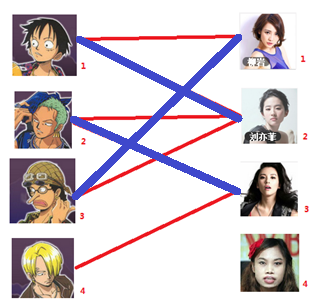
于是乎,第三个男生也找到了女朋友,其他人也没什么损失(大概吧),也都和自己的新女朋友成为情侣,在无后顾之忧,所以去掉黄线。于是此次遍历第三个男生的结果就成了这样。
===============================================================================
遍历到第四个男生:还是尝试着给他找妹子,发现第一个和他相看两不厌的女生(3号女生) 已经有主了,这时候这个第四个男生就直接暴走了,决定和第二个男生抢 3号女生的配偶权。第二个男生抢不过,发现已经再没有女生能够看上她,想到自己可能注孤生,绝望的他,又去找 3号女生,决定再和 第四个男生抢 3号女生的配偶权,最终 第二个男生 战胜 第三个男生,赢得美人青睐,抱得美人归。而第四个男生被赶跑后,发现再没有女生看得上他,无可奈何,孤独终老。
===============================================================================
这就是匈牙利算法的流程,其中找妹子是个递归的过程,也就是算法的核心:寻找增广路径。其意思就是 尝试霸占女生,赶跑原配, 在赶跑其他男生后,这些男生若没有归宿,他们是会找回来报仇,也就是说霸占失败,如果这些男生被赶跑之后还有归宿,则霸占成功。
============ ========== ======== ======= ====== ===== ==== === == =
原文:https://www.cnblogs.com/asdfknjhu/p/13976933.html