树的定义

??树是n(n>=0)各节点的有限集。n=0事称为空树。在任意非空树中：

1. 有且仅有一个特定的称为根的节点
2. 当n>1时，其余节点可分为m个互不相交的有限集T1、T2、······、Tm其中每一个集合又是一棵树，并且称为根的子树如图
   

树的ADT

二叉树

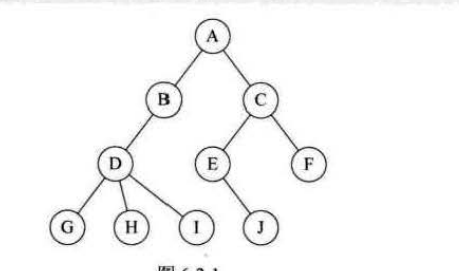
??二叉树是在树的定义下，子树只有左子树和右子树。

??二叉链表的节点结构定义代码

二叉树的遍历方法

前序遍历

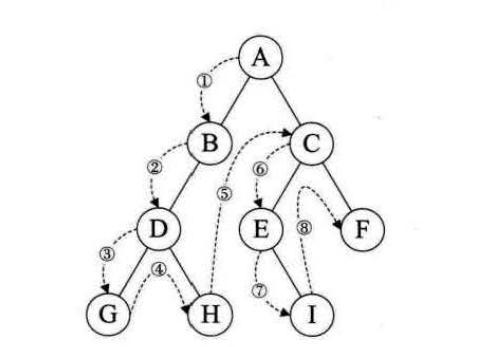
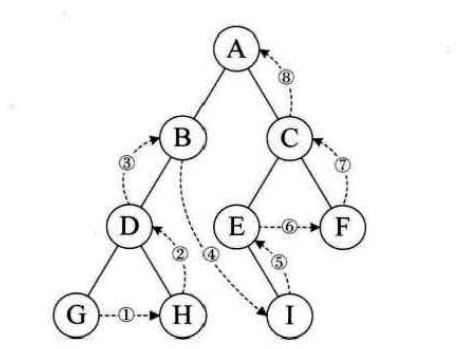
规则是若二叉树为空，则空操作返回，否则先访问根节点，然后前序遍历左子树，在前序遍历右子树，如图，前序遍历为：ABDGHCEIF

遍历算法：
void PreOrderT(Tree T)
{
if (T == NULL)
return;
printf("%c", T->data);
PreOrderT(T->lchild);
PreOrderT(T->rchild);
}

中序遍历

规则是若二叉树为空，则空操作返回，否则从根节点开始（先从根节点开始，不访问根节点），中序变量根节点的左子树，然后访问根节点，在中序遍历根节点的右子树。如图中序遍历为：GDHBAEICF

遍历算法：
void MidOrderT(Tree T)
{
if (T == NULL)
return;
MidOrderT(T->lchild);
printf("%c", T->data);
MidOrderT(T->rchild);
}

后序遍历

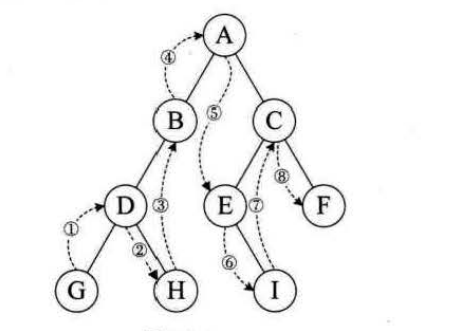
规则是若二叉树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后访问根节点，如图 遍历顺序：GHDBIEFCA

遍历算法：
void PostOrderT(Tree T)
{
if (T == NULL)
return;
PostOrderT(T->lchild);
PostOrderT(T->rchild);
printf("%c", T->data);
}

数据结构---树

原文：https://www.cnblogs.com/cheng-hong/p/13983757.html