给一个有 n 个结点的有向无环图,找到所有从 0 到 n-1 的路径并输出(不要求按顺序)
二维数组的第 i 个数组中的单元都表示有向图中 i 号结点所能到达的下一些结点(译者注:有向图是有方向的,即规定了 a→b 你就不能从 b→a )空就是没有下一个结点了。
示例 1:
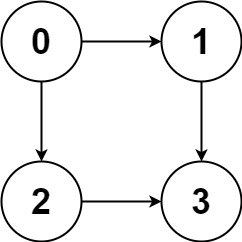
输入:graph = [[1,2],[3],[3],[]]
输出:[[0,1,3],[0,2,3]]
解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2:
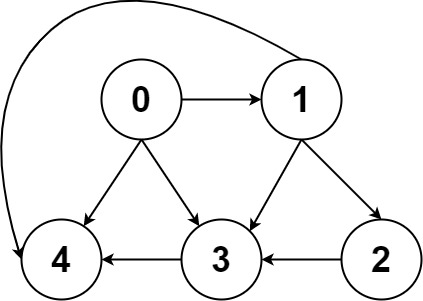
输入:graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
示例 3:
输入:graph = [[1],[]]
输出:[[0,1]]
本题是一道深度优先搜索,在学习数据结构的图的时候,我们都学过这个概念,当然,它很好理解,可是当你写代码的时候,还能像正常思考一样把它快速搞定吗?
本题的基本思路:
1.递归实现
2.创建一个list代表路径,每次递归增加一个节点,该次递归结束后再把这个节点删除(回溯)
3.当最终找到了终点的时候,把list加入到最终的结果中
1 class Solution { 2 public: 3 vector<vector<int>> ret; 4 vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) { 5 if(graph.size()==0) 6 { 7 return ret; 8 } 9 vector<int> list; 10 dfs(0,graph,list); 11 return ret; 12 } 13 void dfs(int curr,vector<vector<int>>& graph,vector<int>& list) 14 //curr代表当前的节点,list代表要传入到ret里面的一个int的向量 15 { 16 list.push_back(curr); 17 if(curr==graph.size()-1)//如果当前节点到达了终点,现在这条list就成功了,可以输入到ret里面了 18 { 19 ret.push_back(list); 20 } 21 for(int i:graph[curr])//递归寻找当前节点的所有可以到达的下一个节点,从而最终可以判断是否能到达终点 22 { 23 dfs(i,graph,list); 24 } 25 list.pop_back();//回溯 26 } 27 };
如果您也是一名刚刚学习到图的初学者,还没实现过深搜,我建议您自己做一遍这道题,这道题是一道非常典型的深度优先搜索题,思路很清晰,有助于您的代码能力的提高。
原文:https://www.cnblogs.com/wangqianming12138/p/13988141.html