AcWing 243. 一个简单的整数问题2 (树状数组,区间更新/询问)

• 题意:区间更新,区间询问.

• 题解;对于区间更新,我们还是用差分数组\(b_i\)来更新,区间询问时,我们的答案是:\(\sum_{i=l}^{r}\sum_{j=1}^{i}b_j\),

  

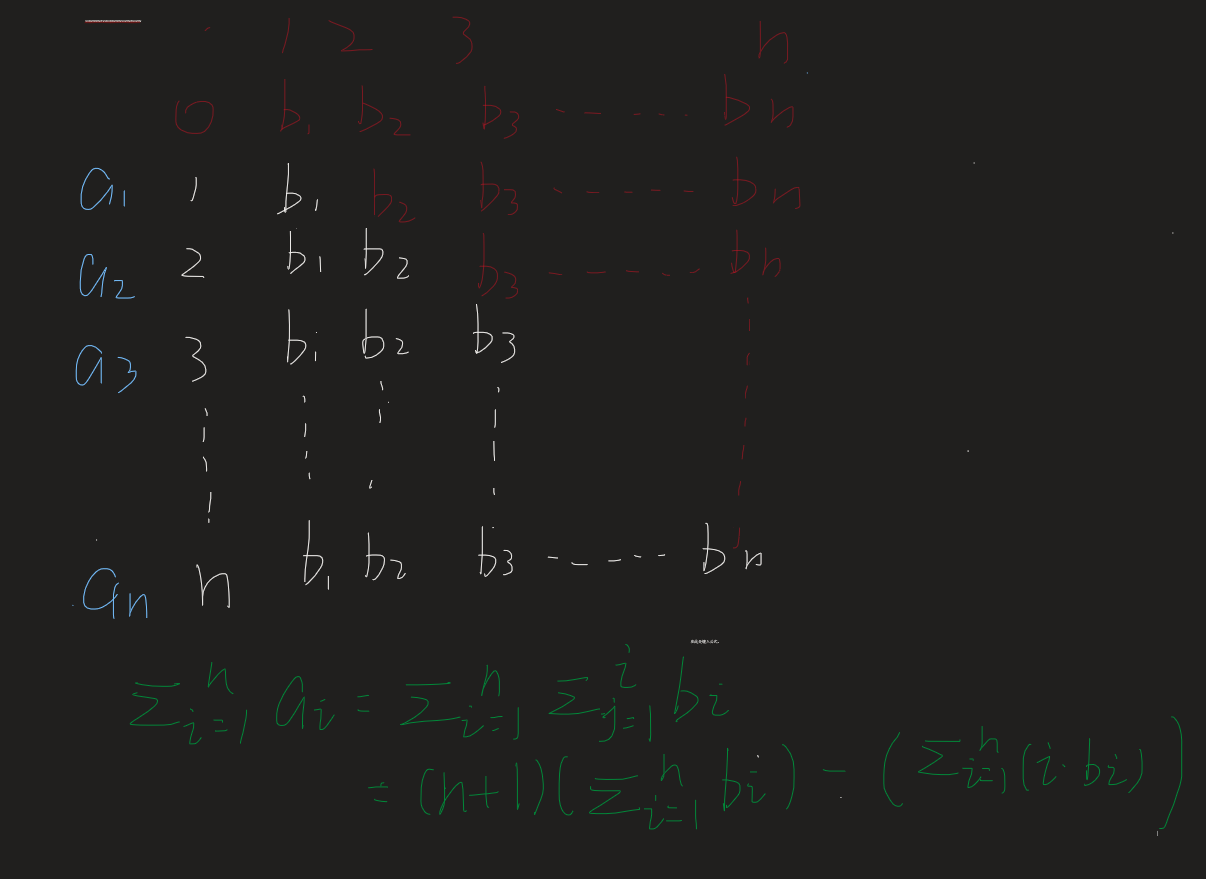
  所以,我们搞两个树状数组维护\(b_i\)和\(i*b_i\)即可.

• 代码:

  #define int long long 
  
  int n,m;
  int a[N];
  int c1[N],c2[N];
  
  int lowbit(int x){
      return x&(-x);
  }
  
  void updata1(int i,int k){
      while(i<=n){
          c1[i]+=k;
          i+=lowbit(i);
      }
  }
  
  void updata2(int i,int k){
      while(i<=n){
          c2[i]+=k;
          i+=lowbit(i);
      }
  }
  
  int get_sum1(int i){
      int res=0;
      while(i){
          res+=c1[i];
          i-=lowbit(i);
      }
      return res;
  }
  
  int get_sum2(int i){
      int res=0;
      while(i){
          res+=c2[i];
          i-=lowbit(i);
      }
      return res;
  }
  
  signed main() {
      ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
      cin>>n>>m;
  
      rep(i,1,n){
          cin>>a[i];
          updata1(i,a[i]-a[i-1]);
          updata2(i,i*(a[i]-a[i-1]));
      }
  
      rep(i,1,m){
          char op;
          cin>>op;
          if(op==‘Q‘){
              int l,r;
              cin>>l>>r;
              int cur1=get_sum1(r)*(r+1)-get_sum2(r);
              int cur2=get_sum1(l-1)*l-get_sum2(l-1);
              cout<<cur1-cur2<<‘\n‘;
          }
          else{
              int l,r,d;
              cin>>l>>r>>d;
              updata1(l,d);
              updata2(l,l*d);
              updata1(r+1,-d);
              updata2(r+1,(r+1)*-d);
          }
      }
  
   
      return 0;
  }
  

AcWing 243. 一个简单的整数问题2 (树状数组,区间更新/询问)

原文：https://www.cnblogs.com/lr599909928/p/13991482.html