Gaussian Mixture Model - Python实现

• 算法特征:
  ①. 高斯分布作为基函数; ②. 多个高斯分布进行凸组合; ③. 极大似然法估计概率密度.
• 算法推导:
  GMM概率密度形式如下:
  \begin{equation}
  p(x) = \sum_{k=1}^{K}\pi_kN(x|\mu_k, \Sigma_k)
  \label{eq_1}
  \end{equation}
  其中, $\pi_k$、$\mu_k$、$\Sigma_k$分别表示第$k$个高斯分布的权重、均值及协方差矩阵, 且$\sum\limits_{k=1}^{K}\pi_k = 1, \forall \pi_k \geq 0$.
  令样本集合为$\{x^{(1)}, x^{(2)}, \cdots, x^{(n)}\}$, 本文拟采用EM(Expectation-Maximization)算法求解上述优化变量$\{\pi_k, \mu_k, \Sigma_k\}_{k=1\sim K}$.
  $step1$:
  随机初始化$\{\pi_k, \mu_k, \Sigma_k\}_{k=1\sim K}$.
  $step2 \sim E\ step$:
  计算第$i$个样本落在第$k$个高斯的概率:
  \begin{equation}
  \gamma_k^{(i)} = \frac{\pi_kN(x^{(i)}|\mu_k, \Sigma_k)}{\sum\limits_{k=1}^{K} \pi_k N(x^{(i)}|\mu_k, \Sigma_k)}
  \label{eq_2}
  \end{equation}
  $step3 \sim M\ step$:
  计算第$k$个高斯的样本数:
  \begin{equation}
  N_k = \sum_{i=1}^{n}\gamma_k^{(i)}
  \label{eq_3}
  \end{equation}
  更新第$k$个高斯的权重:
  \begin{equation}
  \pi_k = \frac{N_k}{N}
  \label{eq_4}
  \end{equation}
  更新第$k$个高斯的均值:
  \begin{equation}
  \mu_k = \frac{\sum\limits_{i=1}^{n}\gamma_k^{(i)}x^{(i)}}{N_k}
  \label{eq_5}
  \end{equation}
  更新第$k$个高斯的协方差矩阵:
  \begin{equation}
  \Sigma_k = \frac{\sum\limits_{i=1}^{n}\gamma_k^{(i)}(x^{(i)} - \mu_k)(x^{(i)} - \mu_k)^{\mathrm{T}}}{N_k}
  \label{eq_6}
  \end{equation}
  $step4$:
  回到$step2$, 直到优化变量$\{\pi_k, \mu_k, \Sigma_k\}_{k=1\sim K}$均收敛.
• 代码实现:
  Part Ⅰ:
  现以如下数据集为例进行算法实施:
  
  

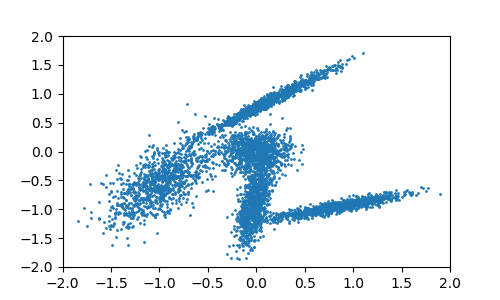
   1 # 生成聚类数据集
   2 
   3 import numpy
   4 from matplotlib import pyplot as plt
   5 
   6 
   7 numpy.random.seed(3)
   8 
   9 
  10 def generate_data(clusterNum):
  11     mu = [0, 0]
  12     sigma = [[0.03, 0], [0, 0.03]]
  13     data = numpy.random.multivariate_normal(mu, sigma, (1000, ))
  14     
  15     for idx in range(clusterNum  - 1):
  16         mu = numpy.random.uniform(-1, 1, (2, ))
  17         arr = numpy.random.uniform(0, 1, (2, 2))
  18         sigma = numpy.matmul(arr.T, arr) / 10
  19         tmpData = numpy.random.multivariate_normal(mu, sigma, (1000, ))
  20         data = numpy.vstack((data, tmpData))
  21     
  22     return data
  23 
  24 
  25 def plot_data(data):
  26     fig = plt.figure(figsize=(5, 3))
  27     ax1 = plt.subplot()
  28     
  29     ax1.scatter(data[:, 0], data[:, 1], s=1)
  30     ax1.set(xlim=[-2, 2], ylim=[-2, 2])
  31     # plt.show()
  32     fig.savefig("plot_data.png", dpi=100)
  33     plt.close()
  34 
  35         
  36 
  37 if __name__ == "__main__":
  38     X = generate_data(5)
  39     plot_data(X)

  View Code

  

  Part Ⅱ:
  GMM实现如下:
  
  

    1 # Gaussian Mixture Model之实现
    2 
    3 import numpy
    4 from matplotlib import pyplot as plt
    5 
    6 
    7 numpy.random.seed(3)
    8 
    9 
   10 
   11 def generate_data(clusterNum):
   12     mu = [0, 0]
   13     sigma = [[0.03, 0], [0, 0.03]]
   14     data = numpy.random.multivariate_normal(mu, sigma, (1000, ))
   15     
   16     for idx in range(clusterNum  - 1):
   17         mu = numpy.random.uniform(-1, 1, (2, ))
   18         arr = numpy.random.uniform(0, 1, (2, 2))
   19         sigma = numpy.matmul(arr.T, arr) / 10
   20         tmpData = numpy.random.multivariate_normal(mu, sigma, (1000, ))
   21         data = numpy.vstack((data, tmpData))
   22     
   23     return data
   24 
   25 
   26 
   27 class GMM(object):
   28     
   29     def __init__(self, X, clusterNum):
   30         self.__X = X                                      # 聚类数据集, 1行代表1个样本
   31         self.__clusterNum = clusterNum                    # 类簇数量
   32         
   33         
   34     def get_clusters(self, pi, mu, sigma):
   35         ‘‘‘
   36         获取类簇
   37         ‘‘‘
   38         X = self.__X
   39         clusterNum = self.__clusterNum
   40         gamma = self.__calc_gamma(X, pi, mu, sigma)
   41         maxIdx = numpy.argmax(gamma, axis=0)
   42         
   43         clusters = list(list() for idx in range(clusterNum))
   44         for idx, x in enumerate(X):
   45             clusters[maxIdx[idx]].append(x)
   46         clusters = list(numpy.array(cluster) for cluster in clusters)
   47         return clusters
   48         
   49         
   50     def PDF(self, x, pi, mu, sigma):
   51         ‘‘‘
   52         GMM概率密度函数
   53         ‘‘‘
   54         val = sum(list(self.__calc_gaussian(x, mu[k], sigma[k]) * pi[k] for k in range(mu.shape[0])))
   55         return val
   56         
   57         
   58     def optimize(self, maxIter=1000, epsilon=1.e-6):
   59         ‘‘‘
   60         maxIter: 最大迭代次数
   61         epsilon: 收敛判据, 优化变量趋于稳定则收敛
   62         ‘‘‘
   63         X = self.__X
   64         clusterNum = self.__clusterNum    # 簇数量
   65         N = X.shape[0]                    # 样本数量
   66         
   67         pi, mu, sigma = self.__init_GMMOptVars(X, clusterNum)
   68         gamma = numpy.zeros((clusterNum, N))
   69         for idx in range(maxIter):
   70             print("iterCnt: {:3d},   pi = {}".format(idx, pi))
   71             gamma = self.__calc_gamma(X, pi, mu, sigma)
   72             
   73             Nk = numpy.sum(gamma, axis=1)
   74             piNew = Nk / N
   75             muNew = self.__calc_mu(X, gamma, Nk)
   76             sigmaNew = self.__calc_sigma(X, gamma, mu, Nk)
   77             
   78             deltaPi = piNew - pi
   79             deltaMu = muNew - mu
   80             deltaSigma = sigmaNew - sigma
   81             if self.__converged(deltaPi, deltaMu, deltaSigma, epsilon):
   82                 return piNew, muNew, sigmaNew, True
   83             pi, mu, sigma = piNew, muNew, sigmaNew
   84             
   85         return pi, mu, sigma, False
   86             
   87             
   88     def __calc_sigma(self, X, gamma, mu, Nk):
   89         sigma = list()
   90         for gamma_k, mu_k, Nk_k in zip(gamma, mu, Nk):
   91             term1 = X - mu_k
   92             term2 = gamma_k.reshape((-1, 1)) * term1
   93             term3 = numpy.matmul(term2.T, term1)
   94             sigma_k = term3 / Nk_k
   95             sigma.append(sigma_k)
   96         return numpy.array(sigma)
   97             
   98             
   99     def __calc_mu(self, X, gamma, Nk):
  100         mu = list()
  101         for gamma_k, Nk_k in zip(gamma, Nk):
  102             term1 = gamma_k.reshape((-1, 1)) * X
  103             term2 = numpy.sum(term1, axis=0)
  104             mu_k = term2 / Nk_k
  105             mu.append(mu_k)
  106         return numpy.array(mu)
  107             
  108             
  109     def __calc_gamma(self, X, pi, mu, sigma):
  110         gamma = numpy.zeros((pi.shape[0], X.shape[0]))
  111         for k in range(gamma.shape[0] - 1):
  112             for i in range(gamma.shape[1]):
  113                 gamma[k, i] = self.__calc_gamma_ik(X[i], k, pi, mu, sigma)
  114         term1 = numpy.sum(gamma[:-1, :], axis=0)
  115         gamma[-1] = 1 - term1
  116         return gamma
  117         
  118             
  119     def __converged(self, deltaPi, deltaMu, deltaSigma, epsilon):
  120         val1 = numpy.linalg.norm(deltaPi)
  121         val2 = numpy.linalg.norm(deltaMu)
  122         val3 = numpy.linalg.norm(deltaSigma)
  123         if val1 <= epsilon and val2 <= epsilon and val3 <= epsilon:
  124             return True
  125         return False
  126         
  127         
  128     def __calc_gamma_ik(self, x_i, k, pi, mu, sigma):
  129         pi_k = pi[k]
  130         mu_k = mu[k]
  131         sigma_k = sigma[k]
  132         
  133         upperVal = pi_k * self.__calc_gaussian(x_i, mu_k, sigma_k)
  134         lowerVal = self.PDF(x_i, pi, mu, sigma)
  135         gamma_ik = upperVal / lowerVal
  136         return gamma_ik
  137     
  138         
  139     def __calc_gaussian(self, x, mu, sigma):
  140         ‘‘‘
  141         x: 输入x - 1维数组
  142         mu: 均值
  143         sigma: 协方差矩阵
  144         ‘‘‘
  145         d = mu.shape[0]
  146         term0 = (x - mu).reshape((-1, 1))
  147         term1 = 1 / numpy.math.sqrt((2 * numpy.math.pi) ** d * numpy.linalg.det(sigma))
  148         term2 = numpy.matmul(numpy.matmul(term0.T, numpy.linalg.inv(sigma)), term0)[0, 0]
  149         term3 = numpy.math.exp(-term2 / 2)
  150         val = term1 * term3
  151         return val
  152         
  153         
  154     def __init_GMMOptVars(self, X, clusterNum):
  155         pi = self.__init_pi(clusterNum)                         # GMM权重初始化
  156         mu = self.__init_mu(X, clusterNum)                      # GMM均值初始化
  157         sigma = self.__init_sigma(X.shape[1], clusterNum)       # GMM协方差矩阵初始化 - 采用单位矩阵初始化之
  158         return pi, mu, sigma
  159         
  160         
  161     def __init_sigma(self, n, clusterNum):
  162         sigma = list()
  163         for idx in range(clusterNum):
  164             sigma.append(numpy.identity(n))
  165         return numpy.array(sigma)
  166         
  167         
  168     def __init_mu(self, X, clusterNum, epsilon=1.e-5):
  169         ‘‘‘
  170         采用K-means方法进行初始化
  171         ‘‘‘
  172         lowerBound = numpy.min(X, axis=0)
  173         upperBound = numpy.max(X, axis=0)
  174         oriMu = numpy.random.uniform(lowerBound, upperBound, (clusterNum, X.shape[1]))
  175         traMu = self.__updateMuByKMeans(X, oriMu)
  176         while numpy.linalg.norm(traMu - oriMu) > epsilon:
  177             oriMu = traMu
  178             traMu = self.__updateMuByKMeans(X, oriMu)
  179         return traMu    
  180         
  181             
  182     def __updateMuByKMeans(self, X, oriMu):
  183         distList = list()
  184         for mu in oriMu:
  185             distTerm = numpy.linalg.norm(X - mu, axis=1)
  186             distList.append(distTerm)
  187         distArr = numpy.vstack(distList)
  188         distIdx = numpy.argmin(distArr, axis=0)
  189         
  190         clusLst = list(list() for i in range(oriMu.shape[0]))
  191         for xIdx, dIdx in enumerate(distIdx):
  192             clusLst[dIdx].append(X[xIdx])
  193         
  194         traMu = list()
  195         for clusIdx, clus in enumerate(clusLst):
  196             if len(clus) == 0:
  197                 traMu.append(oriMu[clusIdx])
  198             else:
  199                 tmpClus = numpy.array(clus)
  200                 mu = numpy.sum(tmpClus, axis=0) / tmpClus.shape[0]
  201                 traMu.append(mu)
  202         return numpy.array(traMu)
  203             
  204         
  205         
  206     def __init_pi(self, clusterNum):
  207         pi = numpy.ones((clusterNum, )) / clusterNum
  208         return pi
  209         
  210         
  211         
  212 class GMMPlot(object):
  213     
  214     @staticmethod
  215     def profile_plot(X, gmmObj, pi, mu, sigma):
  216         surfX1 = numpy.linspace(-2, 2, 100)
  217         surfX2 = numpy.linspace(-2, 2, 100)
  218         surfX1, surfX2 = numpy.meshgrid(surfX1, surfX2)
  219         
  220         surfY = numpy.zeros((surfX2.shape[0], surfX1.shape[1]))
  221         for rowIdx in range(surfY.shape[0]):
  222             for colIdx in range(surfY.shape[1]):
  223                 surfY[rowIdx, colIdx] = gmmObj.PDF(numpy.array([surfX1[rowIdx, colIdx], surfX2[rowIdx, colIdx]]), pi, mu, sigma)
  224         
  225         clusters = gmmObj.get_clusters(pi, mu, sigma)
  226         
  227         fig = plt.figure(figsize=(10, 3))
  228         ax1 = plt.subplot(1, 2, 1)
  229         ax2 = plt.subplot(1, 2, 2)
  230         
  231         ax1.contour(surfX1, surfX2, surfY, levels=16)
  232         ax1.scatter(X[:, 0], X[:, 1], marker="o", color="tab:blue", s=1)
  233         ax1.set(xlim=[-2, 2], ylim=[-2, 2], xlabel="$x_1$", ylabel="$x_2$")
  234         
  235         for idx, cluster in enumerate(clusters):
  236             ax2.scatter(cluster[:, 0], cluster[:, 1], s=1, label="$cluster\ {}$".format(idx))
  237         ax2.set(xlim=[-2, 2], ylim=[-2, 2], xlabel="$x_1$", ylabel="$x_2$")
  238         ax2.legend()
  239         
  240         fig.tight_layout()
  241         # plt.show()
  242         fig.savefig("profile_plot.png", dpi=100)
  243         plt.close()
  244         
  245         
  246         
  247 if __name__ == "__main__":
  248     clusterNum = 5
  249     X = generate_data(5)
  250     
  251     gmmObj = GMM(X, clusterNum)
  252     pi, mu, sigma, _ = gmmObj.optimize()
  253     
  254     GMMPlot.profile_plot(X, gmmObj, pi, mu, sigma)

  View Code
• 结果展示:
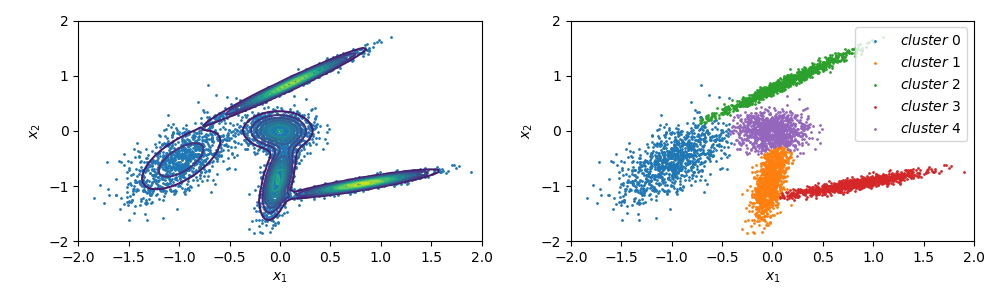  左侧为聚类轮廓, 右侧为簇划分. 很显然, 高斯混合模型适用于高斯型数据分布, 此时聚类效果较为明显.
• 使用建议:
  ①. 由于EM算法只能保证局部最优, 因此选择一个合适的初值较为重要, 本文以K-means结果作为初值进行优化;
  ②. 根据基函数特征, 高斯混合模型适用于高斯型数据分布.
• 参考文档:
  https://baike.baidu.com/item/%E9%AB%98%E6%96%AF%E6%B7%B7%E5%90%88%E6%A8%A1%E5%9E%8B/8878468?fr=aladdin

Gaussian Mixture Model - Python实现

原文：https://www.cnblogs.com/xxhbdk/p/13874439.html