1. 双极型晶体管电流源
引入：在BJT放大电路中，为了使其工作在合适的Q点，可以在BJT的集电极用一个恒流源使这个电路处于一个固定的Q点，如下所示：
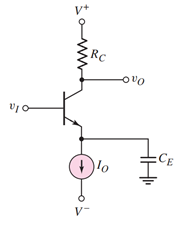
现在的目标是取得这样的一个恒定电流源。
电路原理图：
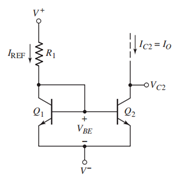
一般来说这样的电路是用两个相同的晶体管制成的，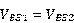
，其
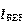的表达式如下：
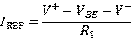
左边的晶体管由于基极和集电极相连，它一定处于正向放大状态，那么如果右边的也处于正向放大状态，可以分析得到：
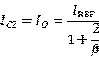
因为
比较大，这样的晶体管电路可以使得
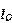和
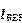比较接近。
但是这样的表达式其实是没有考虑到厄利效应的，当厄利电压不为无穷大时，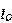
和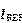
的关系修正为：
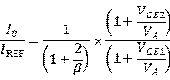
存在厄利效应时，我们知道输出电流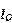
是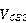
的函数，那么
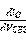就是一个重要的研究对象，对上面的式子求导，可以得到以下表达式：
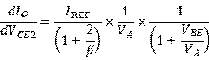
其中如果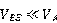
（大部分时候都应该如此，
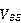是0.几伏的数量级，
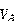是几十几百伏的数量级），那么这个表达式还可以简化为：
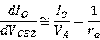
这个公式可以用来求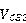
的变化量所导致的
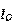变化量，只需把式子看成是一个微商的形式即可。
这样的电压源电路，接上引言所提到的放大电路，就是下面这个样子（框内为那部分放大电路）：
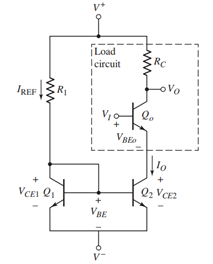
电路原理图：
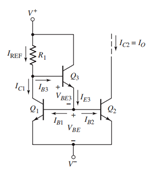
此时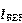
被晶体管基极分走的流更少了，经过分析可以有：
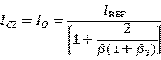
其中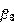
为新加入的晶体管的电流放大倍数，这样的设计可以使得
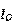和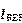
更加接近。这里的
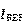可以由以下表达式给出：
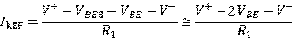
这个电流源的输入电阻和双晶体管电流源的输出电阻相同，都是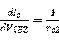
，其中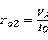
，这使得这样的电流在两个晶体管存在失配的情况下会使得其输出电流很容易偏离其理想值。因此应该作出一些改进。
1.2.2 共射-共基电流源
电路原理图：
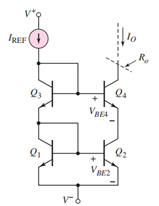
其输出电阻为：
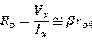
电路原理图：
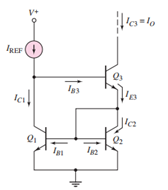
其输出电流和输入电流之间的关系为：
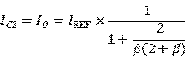
其输出电阻为：
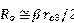
前面介绍过的电流源电路中，负载电流都可以近似地看作等于基准电流。以双晶体管电流源为例，如果需要的电流是μ级别的，那么所需要的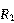
阻值将会特别大，这在集成电路制造上是不实际的。
现在的问题在于，我们的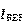 
太大了，但是所需要得到的
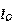又太小了，需要一种电路，把负载电流
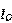缩小，帮助治疗一下，维德拉电流源就是个好东西。
电路原理图：
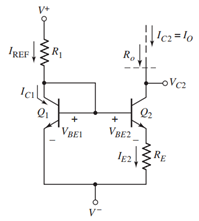
这个电路图中，由于存在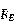
的分压，导致
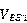大于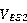
使得输出的负载电流
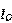更小，经过电路分析后其表达式如下：
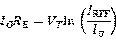
其输出电阻为：
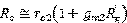
比双晶体管电流源电路大了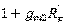
倍。
多晶体管电流镜原理图：
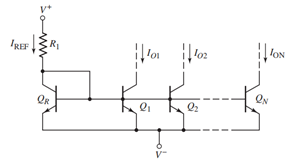
这样的电路可以多路输出同样大小的电路，十分地方便，其表达式为：
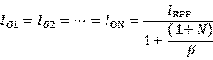
多输出晶体管电流源原理图：
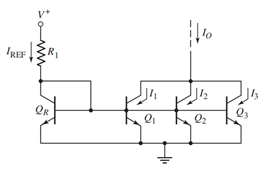
这样的输出可以把各个晶体管的输出累加起来，得到一个很大的输出，其输出为：
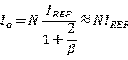
像这种多二极管并联的电路可以用下面的电路符号来简化表示：
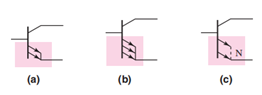
电路原理图：
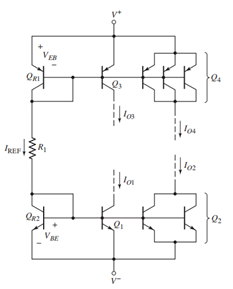
这样的电路里面包含四个输出端子，由于晶体管的
比较大就可以忽略基极电流的影响，这样就有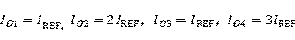
，而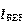
由以下表达式确定：
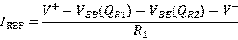
3. 含有源负载的电路：
引入：如果使用传统的双极型放大电路，那么在设置好电路的偏置电压值之后，其电压增益也就随之确定，这样的电路不够灵活。如果把集电极电阻换成一个我们上面学过的电流源，就能更好地控制增益。
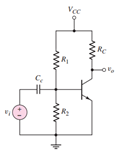
3.1 BJT有源负载电路的直流分析：
电路原理图：
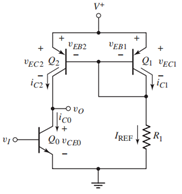
这个电路的输出电压为：
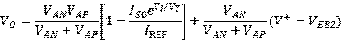
这样的放大器，相比于传统的放大器提高了相当大的增益，而只要晶体管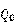
和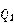
都工作在正向放大模式，以上式子就必定成立，其需要满足的关系式如下:
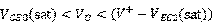
由于这个电路的电压增益特别大，这意味着BJT更加容易进入饱和，由其电压传输特性曲线便可以看出：
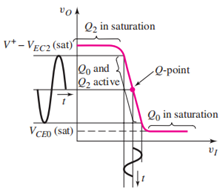
经过电路分析，可以求出其电压增益近似为：
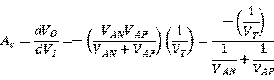
4. 有源负载电路的小信号分析：
BJT有源负载的小信号分析：
为了简化问题，应该把有源负载化为从集电极看进去的电阻大小。
对于BJT有源负载电路而言，其小信号等效电路如下：
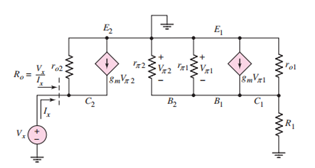
由于在这样的电路中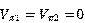
，可以求得集电极看进去的等效电阻为：
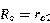
如果在电路上外接负载，如下图所示：
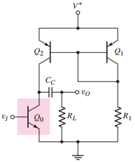
那么其等效电路图可以写成：
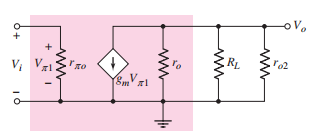
求得其小信号电压增益为：
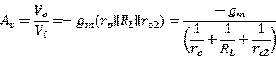
用厄利电压来表示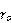
和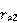
，可以由以下结论：
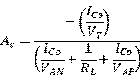
原文：https://www.cnblogs.com/Kiensiyiu/p/13993423.html