分析——比较平均值——单因素ANOVA检验
检验不同学历的人在收入上是否有显著差异
因子(自变量):学历 因变量:收入
点击事后比较(即两两比较),选择方差检验方法
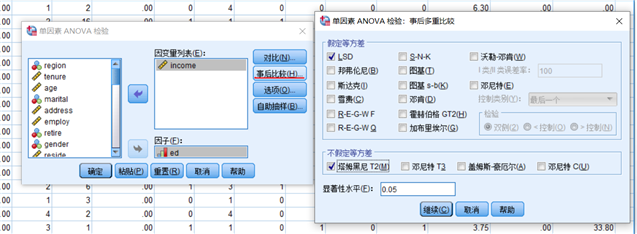
点击选项,勾选描述、方差齐性检验、平均值图
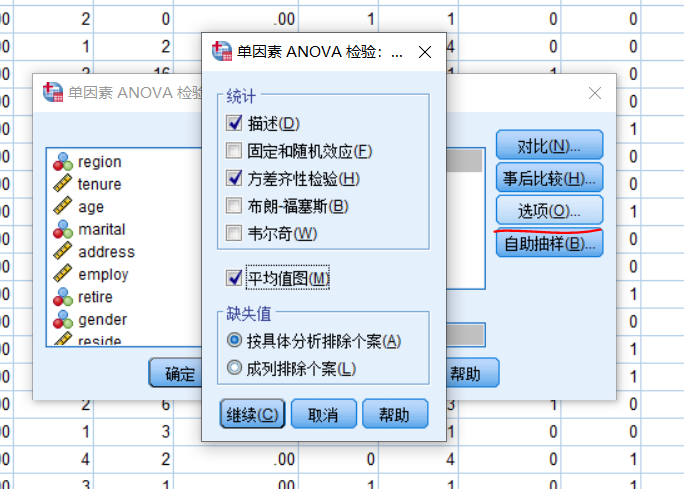
输出结果:
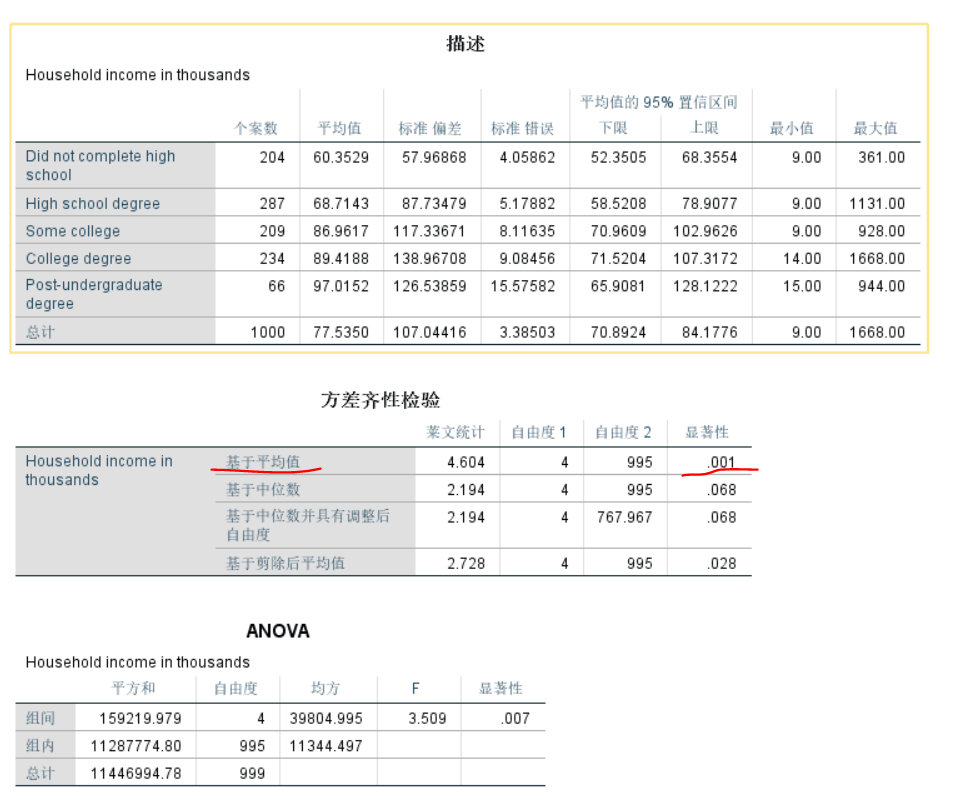
方差齐性检验基于平均值(因为方差检验比较的就是均值)的检验结果的P值=0.001<0.05,拒绝H0,不同学历的人的收入存在显著差异。
各组方差相同的前提不成立,ANOVA检验是否显著没有意义
那去看事后检验的结果吧
在操作时,方差不等的情况下采用塔姆黑尼方法,所以直接看这里就好了
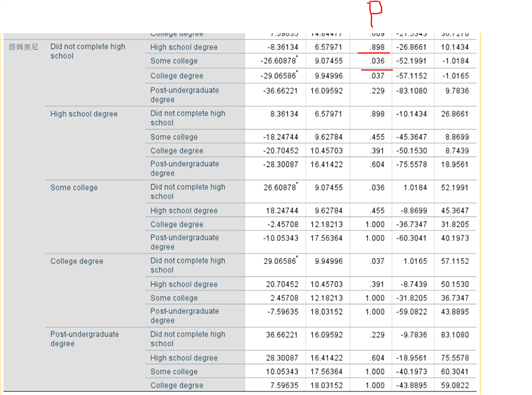
例如:高中以下学历和高中学历两两比较的P=0.898>0.05,高中毕业和高中未毕业人群的收入不存在显著差异
高中以下学历和大专学历两两比较的P=0.036<0.05,高中以下学历和大专学历人群的收入存在显著差异
可是我们又想看总体怎么办呢——非参数检验
分析——非参数检验——k个独立样本
要对学历定义范围:1-5
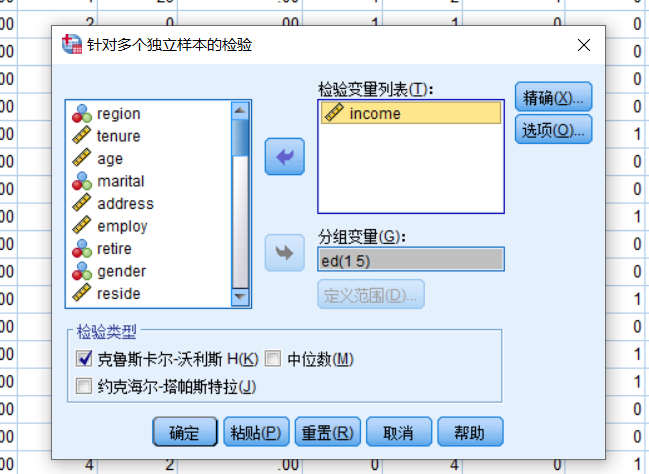
输出结果:
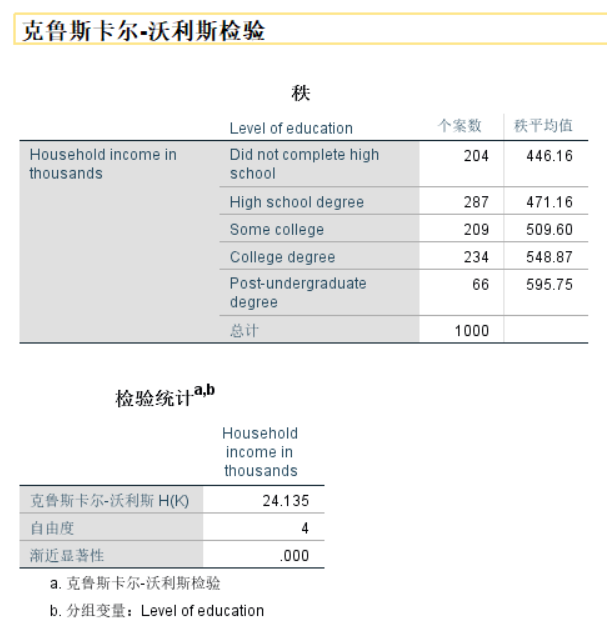
P=0.00<0.05,拒绝H0,接受研究假设,即5个不同学历的独立样本在收入上有显著差异
分析——一般线性模型——单变量(指单个因变量)
固定因子(自变量):学历、性别 注:固定因子的所有可能情况必须在样本中全部包含,否则应该选为随机因子
协变量:是一个要控制的、对因变量有影响的连续变量
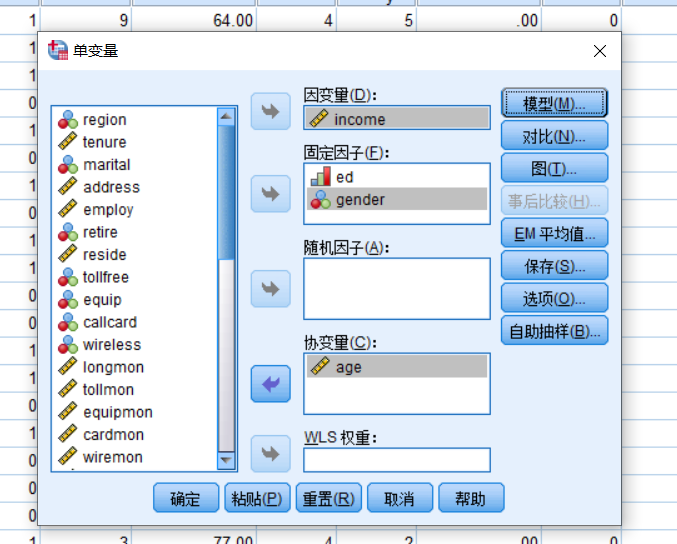
模型——选择
全因子:既考虑所有自变量对因变量的直接效应,又考虑所有分类变量的交互作用对因变量的影响
定制模型:根据研究者需求,定制要考虑的对因变量的影响因素。比如只考虑自变量的直接效应,或部分自变量的交互作用
当自变量特别多(尤其是分类自变量特别多)时,且样本量不多时,应使用定制模型
原因:所有交互作用都考虑进去可能太多了,而且很难解释结果
这里定制模型,只考虑学历和性别的交互作用
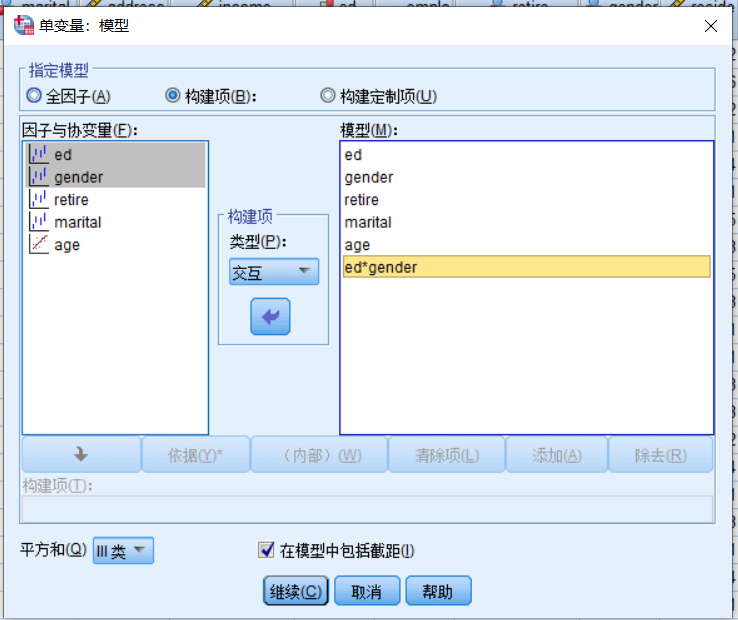
输出结果:
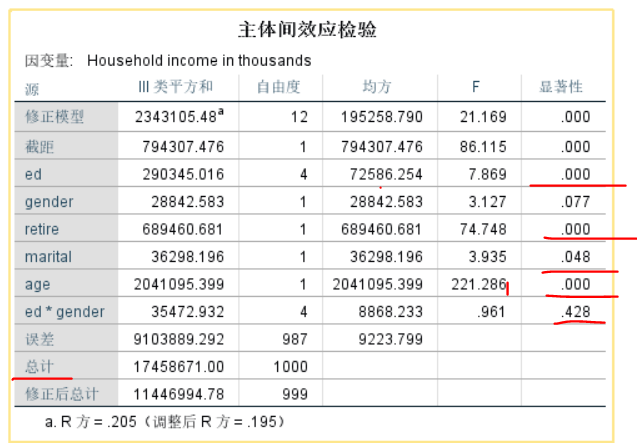
根据P值可以看出,对收入有影响的因素是学历、是否退休、是否结婚、年龄。性别和学历的没有交互作用,即性别*学历的10中人群在收入上没有显著差异
原文:https://www.cnblogs.com/keepgoingyu/p/13997522.html