人工智能本质上也是为了模仿人脑的神经元所设计的,人脑的神经元如下图所示:
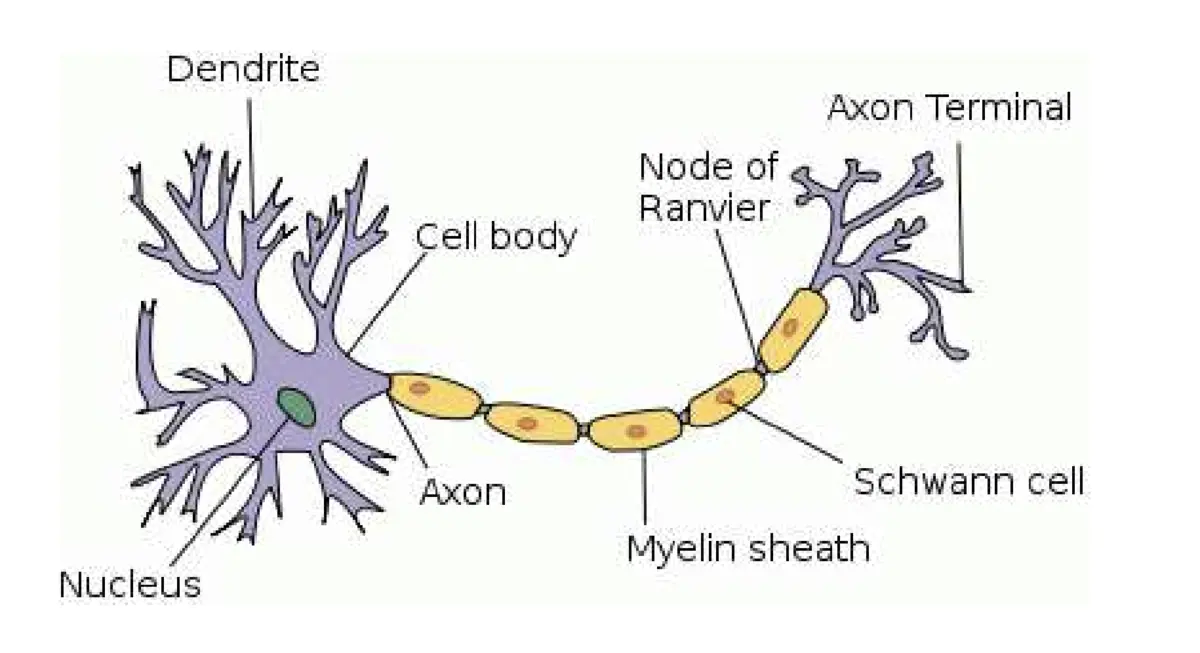
树突(Dendrite) 作为接收端, 然后经过体细胞(cell body)的处理,每当输入端达到一定的阈值(threshold)最后通过轴突(axon)输出.
事实上在人工智能中的感知器(perception)中同样采用了如此类似的结构,大体离不开三样:
- 输入端(input edges): 负责将数据的输入
- 输出端(output edges): 负责输出的输出
- 激活层(activation level): 负责数据的转换, 后续将以
g()函数表示
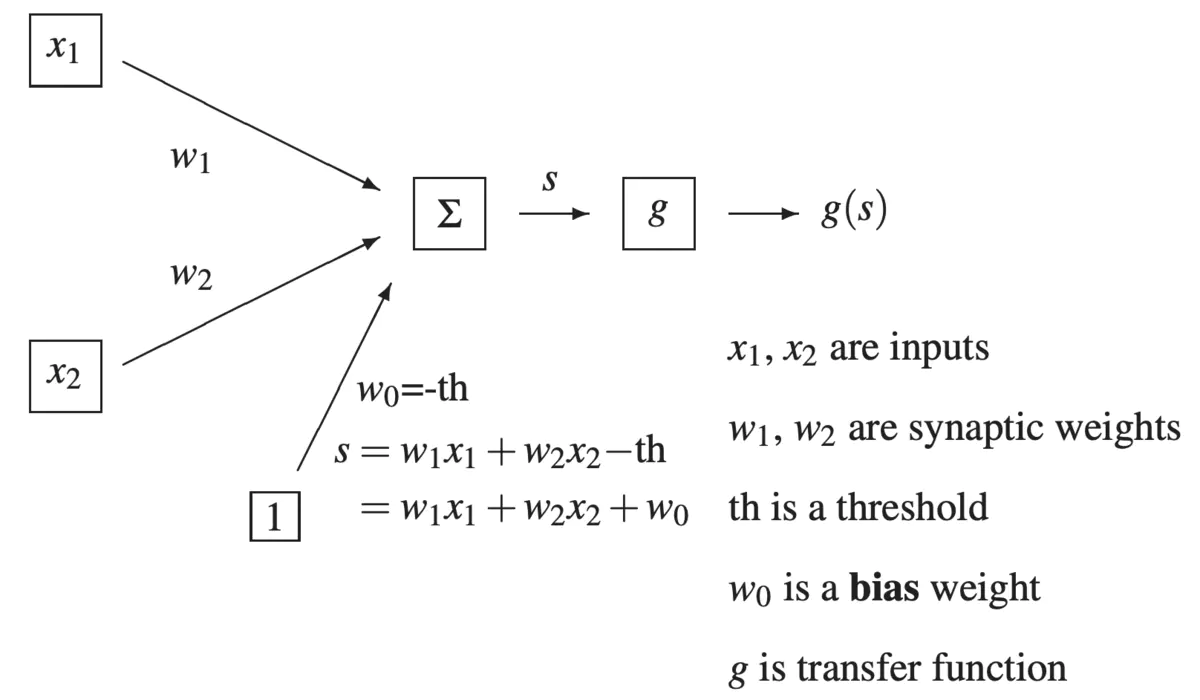
- \(x_1\) 和 \(x_2\)将作为输入,它俩有各自的权重分别为\(w_1\)和\(w_2\)
- \(w_0\)作为偏差权重(bias weight), 可以让模型有效的适配更广的情况, 深层了解请参考: https://www.zhihu.com/question/68247574
- 将输入值按照函数 \(w_1*x_1 + w_2*x_2 + w_0\)计算出总和值 \(\sum\)
- \(\sum\) 将经过转换函数(transfer function)
g()以后得到最终的结果tips: 最简单的转换函数就是当求得的结果大于0则记为1, 反之小于0则记为0,不过你可以设定自己的转换函数
如果我们有一个初始值为如下的模型
| Training example | \(x_1\) | \(x_2\) | 类型 |
|---|---|---|---|
| a | 0 | 1 | -1 |
| b | 2 | 0 | -1 |
| c | 1 | 1 | +1 |
并采用如下的初始值
- \(w_0 = 1.5\)
- \(w_1 = 0\)
- \(w_2 = 2\)
则我们就可手动模拟训练过程
| 序列 | \(w_0\) | \(w_1\) | \(w_2\) | Training example | \(x_1\) | \(x_2\) | 类型 | \(s=w_0+w_1x_1+w_2x_2\) | 需要的处理 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -1.5 | 0 | 2 | a | 0 | 1 | -1 | +0.5 | 相减 |
| 2 | -2.5 | 0 | 1 | b | 2 | 0 | -1 | -2.5 | 无 |
| 3 | -2.5 | 0 | 1 | c | 1 | 1 | +1 | -1.5 | 相加 |
| 4 | -1.5 | 1 | 2 | a | 0 | 1 | -1 | +0.5 | 相减 |
| 5 | -2.5 | 1 | 1 | b | 2 | 0 | -1 | -0.5 | 无 |
| 6 | -2.5 | 1 | 1 | c | 1 | 1 | +1 | -0.5 | 相加 |
| 7 | -1.5 | 2 | 2 | a | 0 | 1 | -1 | +0.5 | 相减 |
| 8 | -2.5 | 2 | 1 | b | 2 | 0 | -1 | +1.5 | 相减 |
| 9 | -3.5 | 0 | 1 | c | 1 | 1 | +1 | -2.5 | 相加 |
| 10 | -2.5 | 1 | 2 | a | 0 | 1 | -1 | -0.5 | 无 |
| 11 | -2.5 | 1 | 2 | b | 2 | 0 | -1 | -0.5 | 无 |
| 11 | -2.5 | 1 | 2 | c | 1 | 1 | +1 | +0.5 | 无 |
至此我们找到了一条能够正确分隔这3个点的权重\(w_0, w_1,w_2\),也就是一条线,这也是perception最本质上的用处:
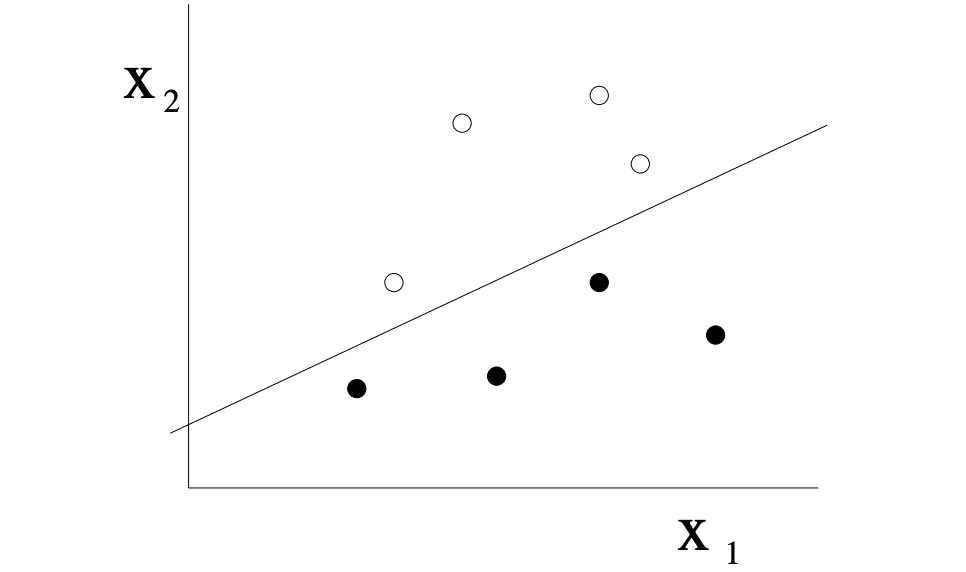
应用在现实生活中, 举个特别简单的例子,你可以理解为图中的白点为性别男,图中的黑点为性别女,perception可正确的将男女分开, 可perception的用处不仅局限于此,任何能用一根线来做分别的都可以用到perception
https://www.zhihu.com/question/68247574 :bias weight有什么用?
原文:https://www.cnblogs.com/garyupup/p/14018642.html