几大排序算法的理解和代码实现（超级详细的过程）

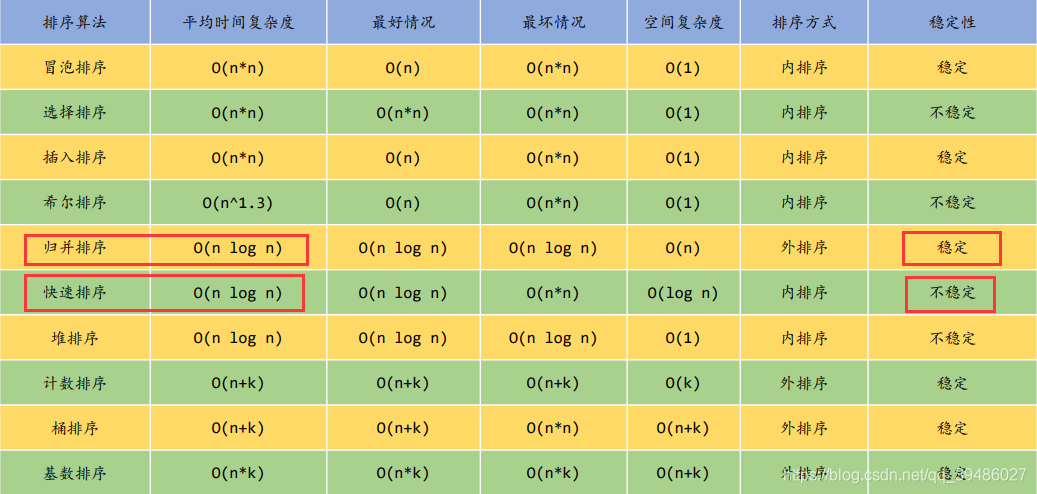
几种常见的排序（比较）

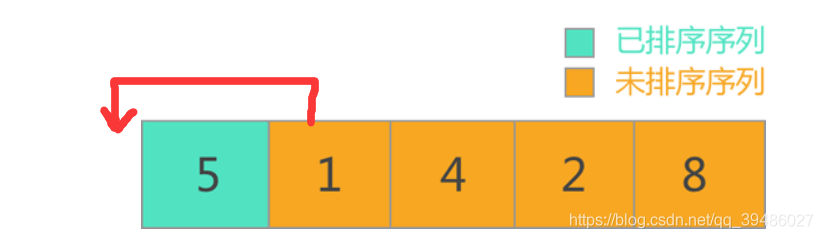
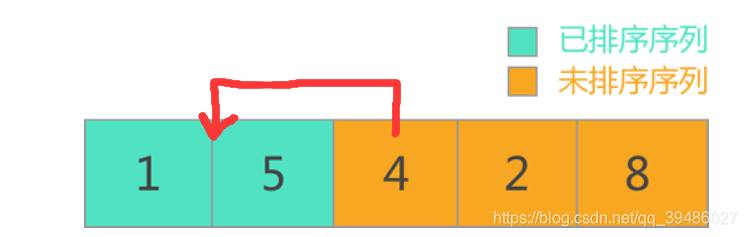
冒泡排序

这里就按照下面的两步模拟冒泡排序： 后面的类似，就不展示。

Code:

#include <iostream>
using namespace std;

const int ARRAY_SIZE = 10;

int BubbleSort(int a[], int size)
{
    for(int i=0; i<size; i++)
        for(int j=0; j<size - i - 1; j++)   // 下面每一次循环少1
            if(a[j] > a[j + 1])
            {
                int tmp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = tmp;
            }
}

int main()
{
    int arr[ARRAY_SIZE] = {49,38,65,1,2,97,76,13,27,49};
    BubbleSort(arr, ARRAY_SIZE);
    for(int i=0; i<ARRAY_SIZE; i++)
    {
        cout<< arr[i] << ‘ ‘;
    }
    return 0;
}

选择排序

选择排序算法是每次选择最小的元素和交换元素来达到排序目的，主要的排序流程：

（1）从原始数组中选最小的元素，将其和位于第1个位置的元素交换。

（2）接着从剩下的n-1个数据中选择次小的1个元素，将其和第2个位置的数据交换

（3）然后，这样不断重复，直到最后两个数据完成交换。最后，便完成了对原始数组的从小到大的排序。

Code

#include <iostream>
using namespace std;

const int ARRAY_SIZE = 10;

void SelectSort(int a[], int size)  
{
	for (int i = 0; i < size; i++) {
		int idx = i;
		for (int j = i; j < size; j++) 
			if (a[idx] > a[j])  	idx = j;
		if (idx != i)    swap(a[i], a[idx]);

	}
}

int main()
{
    int arr[ARRAY_SIZE] = {49,38,65,1,2,97,76,13,27,49};
    SelectSort(arr, ARRAY_SIZE);
    for(int i=0; i<ARRAY_SIZE; i++)
    {
        cout<< arr[i] << ‘ ‘;
    }
    return 0;
}

插入排序

**插入排序的关键点：

（1）前面的是已经排好序的数组， 最后一个数字是待插入的数据。

（2）将待插入的数据插入到前面正确的位置**

Code:

#include <iostream>
using namespace std;

const int ARRAY_SIZE = 10;

void InsertSort(int a[], int size)
{
	for (int i = 0; i < size; i++)
		for (int j = i; j > 0; j--)
			if (a[j] < a[j-1])
				swap(a[j], a[j - 1]);
}

int main()
{
    int arr[ARRAY_SIZE] = {49,38,65,1,2,97,76,13,27,49};
    InsertSort(arr, ARRAY_SIZE);
    for(int i=0; i<ARRAY_SIZE; i++)
    {
        cout<< arr[i] << ‘ ‘;
    }
    return 0;
}

希尔排序

希尔排序 通常也被叫做三个for，一个if。 但是时间复杂度并不是 O（n^3），不清楚的可以看上面。

希尔排序主要的是对待排序数组进行分组， 然后将组间距一步一步缩小，达到最后一步为1，就完成排序。

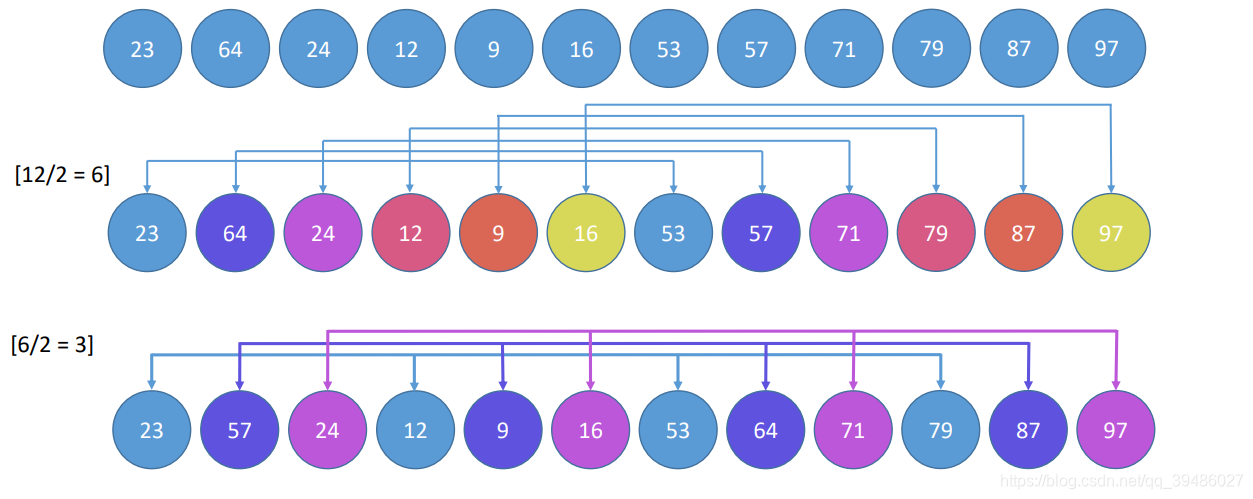
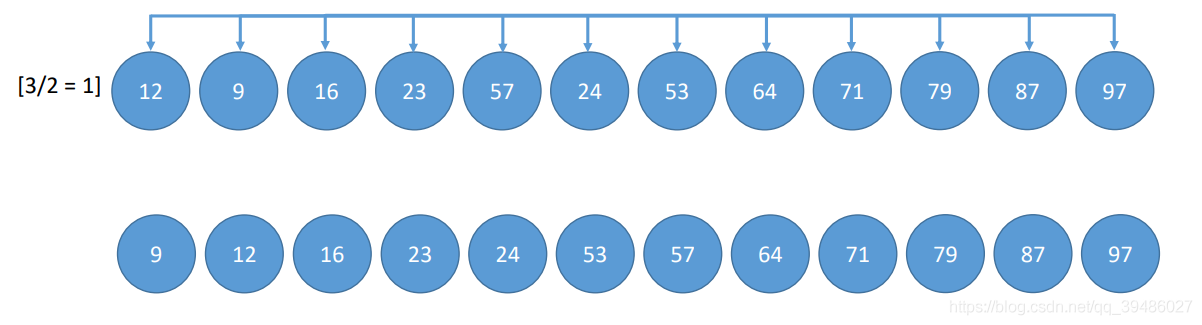
Code

void ShellSort(int a[], int size)
{
    for(int gap = size/2; gap >=1; gap /= 2)
        for(int i = gap; i<size; i++)
            for(int j = i - gap; j>=0; j -= gap)
                if(a[j] > a[i])   //  小的在前面才交换
                    swap(a[i], a[j]);
}

快速排序

利用双指针算法，进行的快速排序。

原理：

1. 先找一个哨兵， 然后利用左指针，发现如果比它小的，直接向后移动指针；
2. 如果发现比哨兵大的元素， 交换位置， 然后在跟右指针元素比较，
3. 如果发现右指针的元素大的，右指针向前移动，如果小于哨兵，交换位置，在跟左指针比较
4. 重复上面的操作，知道左右指针重合。
5. 然后将哨兵左边的元素和右边的元素进行上面的操操作即可。

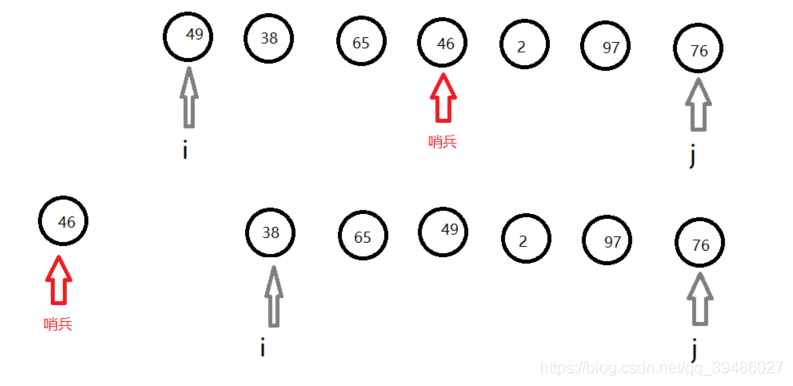
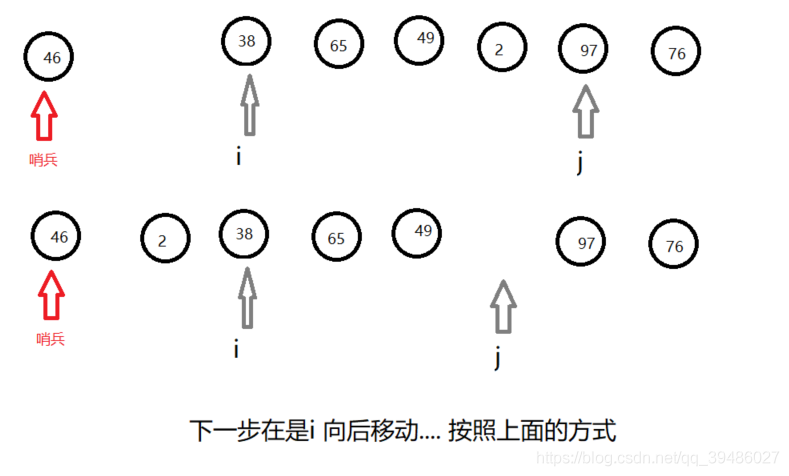
Code

#include <iostream>
using namespace std;

const int N = 100010;
int f[N];
int n;
void quick_sort(int q[], int l, int r)
{
    int i = l-1, j=r+1, x = q[l+r>>1];
    if (l >= r) return ;
    while(i<j)
    {
        do i++; while(q[i] < x);
        do j--; while(q[j] > x);
        if(i < j) swap(q[i], q[j]);
    }
    quick_sort(q,l,j);
    quick_sort(q,j+1,r);
}

int main()
{
    cin >> n;
    for(int i=0; i<n; i++) cin >> f[i];
    quick_sort(f, 0, n-1);
    for(int i=0; i<n; i++) cout << f[i] << " ";
    
    
    return 0;
}

归并排序

归并相对比上面的快排， 类似将分治写在前面了。

Code

#include <iostream>
using namespace std;
const int N = 100010;
int q[N], tmp[N];
int n;

void merge_sort(int q[], int l, int r)
{
    if(l >= r) return ;
    int mid = l + r >> 1;
    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
     int k = 0, i = l ,j = mid + 1;
     while(i <= mid && j <= r)
     {
         if(q[i] <= q[j]) tmp[k++] = q[i++];
         else tmp[k++] = q[j++];
     }
     while(i <= mid) tmp[k++] = q[i++];
     while(j <= r) tmp[k++] = q[j++];
     for(int i=l,j=0; i<=r; i++) q[i] = tmp[j++];
}

int main()
{
    cin >> n;
    for(int i=0; i<n; i++) cin >> q[i];
    merge_sort(q, 0, n-1);
    for(int i=0; i<n; i++) cout << q[i] << ‘ ‘;
    return 0;
    
}

堆排序

堆：完全二叉树 + 满足某种条件（小根堆： 父亲结点比左右儿子小，大根堆： 父亲结点比左右儿子大）

堆和队列有相似地方，在堆底插入元素，在堆顶取出元素，但是堆中元素的排列不是按照到来的先后顺序，而是按照一定的优先顺序排列的

下面讲解小根堆：

root节点是最小的 == 堆顶是最小的元素。 每个点都满足小于左右两个节点的值。

我们想要的堆最好拥有下面几个功能。

1. 插入一个数

2. 求集合中的最小值

3. 删除最小值

4. 删除集合中任意一个数

5. 修改集合中任意一个数

C++ 中的STL中的priority_queue已经有功能 1,2,3

思考：

如何存储堆？

1. 使用一维数组，下标存1到n （这样可以根据数据关系找左右儿子）
2. 根结点下标index为1 （不建议从0开始）
3. x的左儿子下标为2x
4. x的右儿子下标为2x+1

有了上面的思考，我们定义一个down 操作（向下移）和up操作（向上移）， 基本就可以完成上面几种操作。 上面的down 操作和up操作都和树的高度成正比， 因此时间复杂度是O（logn）的。

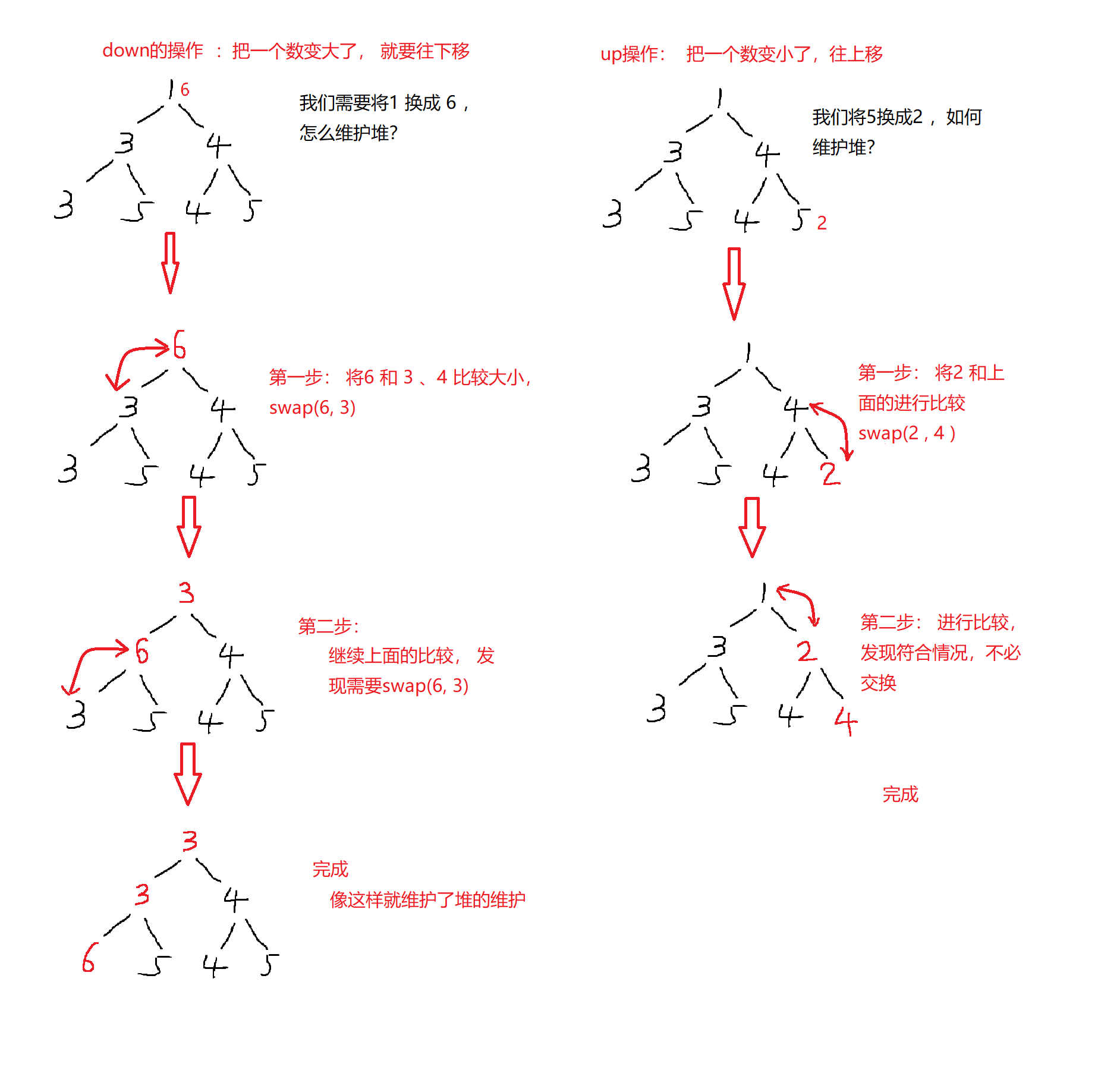
有了上面的思路: 我们看上面5点，是如何实现的。

cnt 表示堆中元素的个数

1. 插入一个数 heap[++ cnt ] = x; up (cnt); // 将插入的最后一个元素上移

2. 求集合中的最小值 heap[1]

3. 删除最小值 heap[1] = heap[cnt] ; cnt -- ; down(1);

4. 删除集合中任意一个数 heap[k] = heap[cnt] ; cnt -- ; down(k), up(k);

5. 修改集合中任意一个数 heap[k] = x; down(k), up(k);

问题：

为什么从1 开始？

因为从0 开始，数组就不满足左右儿子中的数学公式性质了， 当x = 0， 的话左儿子按照数学公式算的话，就是本身了，这个不符合情况。所以数组下标从1 开始。

为什么删除元素需要 将尾节点 覆盖头结点呢？

因为一维数组中，删除头结点非常困难，删除尾节点的话， 十分容易，利用这性质，我们只需要尾节点覆盖头节点后，向下进行diwn操作就可以了。

Code:

我们在排序过程中可以看上面不需要进行up操作， 在下面的我给出将数组进行排序，并输出前m小的元素。

#include <iostream>
using namespace std;

const int N =  100010;
int n,m;
int h[N], cnt;

void down(int u)
{
    int t = u;  // 用t保存 最小的数字
    if(u * 2 <= cnt && h[u * 2] < h[t])  t = u * 2;   // 保证左儿子存在， 并且左儿子小于父亲
    if(u *2 + 1<= cnt && h[u * 2 + 1] < h[t] ) t = u * 2 + 1; // 保证右儿子存在， 并且右儿子小于当前的小的点
    if(u != t)    // 说明根节点不是最小值， 需要交换
    {
        swap(h[t], h[u]);  // 交换使得最小值在上面
        down(t);
    }
}

int main()
{
    cin >> n >> m;  
    for(int i = 1; i<=n; i++) cin >> h[i];
    cnt = n;
    
    for(int i = n/2; i; i--) down(i);       // 初始化堆，从n / 2开始
    
    while(m--)  // 取出前m个小的数字
    {
        cout << h[1] << ‘ ‘;   // 取出小根堆的最小数字
        h[1] = h[cnt];  // 将堆底元素（最后一个）放在第一位置
        cnt --;         // 总的个数 - 1
        down(1);        // 向下调整堆，维护使得最上面元素是最小的元素
    }
    return 0;
}

kmp算法

在面试中的应用

暴力做法

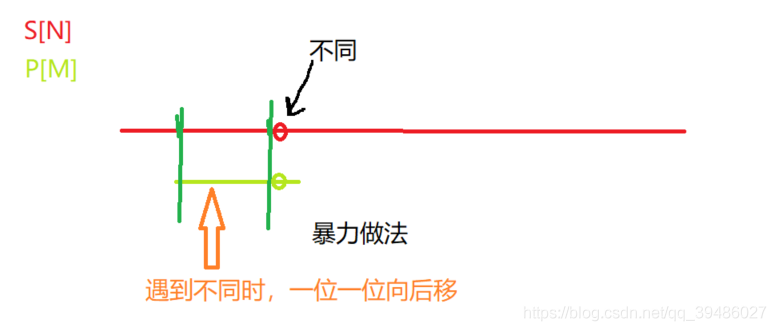
首先我们思考暴力做法的是如何的？

思路： 我们在长的字符串中从前往后遍历的，然后在短的字符串中从前往后遍历，逐个比较，这样就可以找出在长串中是否包含子串了。

Code

这里的时间复杂度就为 O（n*m）了

// s[N]   长串
// p[M]   短串
for(int i = 1; i <= n; i++) {
    bool flag = true;
    for(int j = 1; j <= m；j++) 
        if(s[i+j-1] != p[j]) 
        { 
            flag = false;
            break;
        }
}

优化做法 ： KMP 算法

kmp算法就是三位大牛级别的人针对上面的算法做的一个优化，将时间复杂度转换为了O(n + m).

下面是kmp 的基本比较思路。

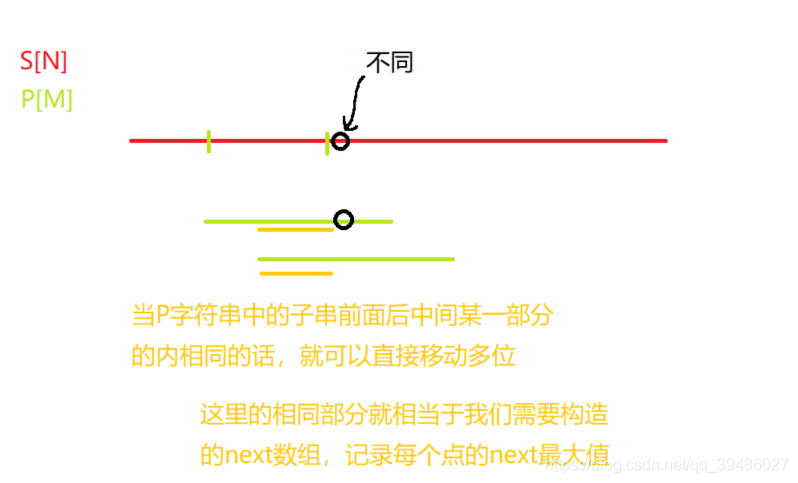
kmp 中 next数组的一个重要的理解点

next 数组是关键；

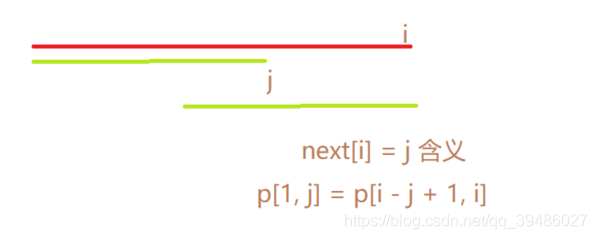
先看下面的这个 前缀和后缀的定义:

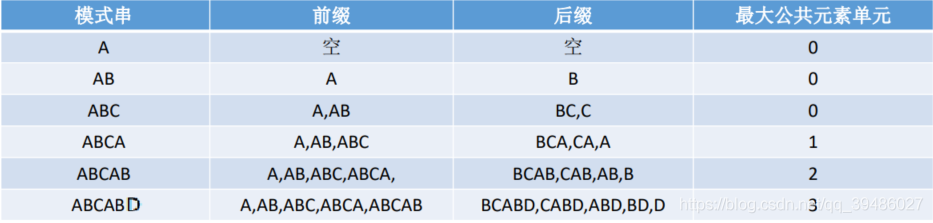
在下面给大家看看 next数据表示的字符串的数组里面的值的例子：

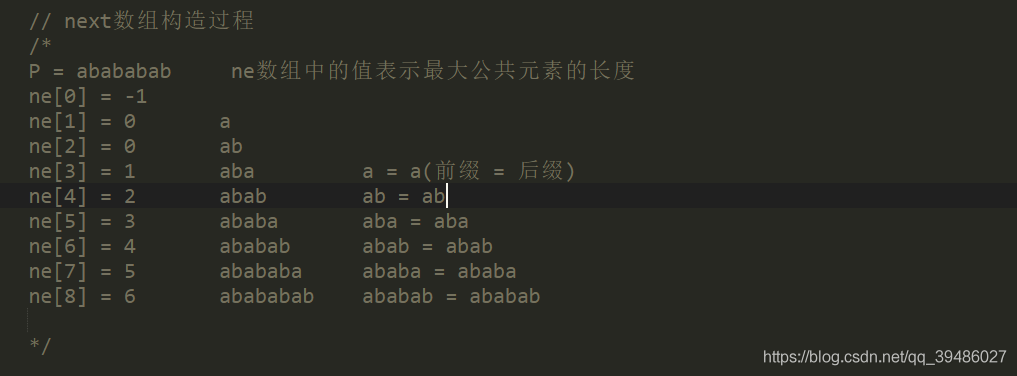
下面是手绘的，自己定义 比较字符串 s[i] 和 p[j + 1] .如果不同的话， j应该移动到哪。

Code

kmp 匹配过程代码

#include <iostream>
using namespace std;
const int N = 10010, M = 100010;
int n,m;
char s[M], p[N];  // s大串， p 小串
int ne[N];   // 小串的next数组

int main()
{
    cin >> n >> p+1 >> m >> s + 1;
    
    // kmp 匹配过程   i从大串1 开始， j从0开始， 比较i 和 j + 1
    for(int i= 1,j = 0; i<=m; i++)
    {
        // 表示j 没有退回起点， 如果s的i个位置和p的j+1位置不匹配 ，直接进行ne数组调到指定位置
        while(j && s[i] != p[j + 1]) j = ne[j];
        if(s[i] == p[j+1] ) j++;    // 如果匹配， j就向后移动
        if(j == n)
        {
            // 匹配成功
        }
    } 
    return 0;
}

kmp next 数组构造过程

    // next 从2开始， 1如果失败了，直接从0开始算。
    for(int i = 2, j = 0; i<=n; i++)   // 因为p数组都是从1开始赋值的 这里的i = 1
    {
        while(j && p[j+1] != p[i]) j = ne[j];   // 这里的j > 0, 如果不满足相等， 就需要跳
        if(p[i] == p[j + 1] )   j++;
        ne[i] = j;
    }

全部代码

输入样例：

3

aba

5

ababa

输出样例：

0 2

#include <iostream>
using namespace std;
 
const int N = 10010, M = 100010;
int n,m;
char s[M], p[N];  // s大串， p 小串
int ne[N];   // 小串的next数组

int main()
{
    cin >> n >> p+1 >> m >> s + 1; 
    // next数组构造过程
    /*
    P = abababab     ne数组中的值表示最大公共元素的长度
    ne[0] = -1
    ne[1] = 0       a
    ne[2] = 0       ab  
    ne[3] = 1       aba         a = a(前缀 = 后缀)
    ne[4] = 2       abab        ab = ab
    ne[5] = 3       ababa       aba = aba   
    ne[6] = 4       ababab      abab = abab
    ne[7] = 5       abababa     ababa = ababa
    ne[8] = 6       abababab    ababab = ababab
   */
    
    // next 从2开始， 1如果失败了，直接从0开始算。
    for(int i = 2, j = 0; i<=n; i++)   // 因为p数组都是从1开始赋值的 这里的i = 1
    {
        while(j && p[j+1] != p[i]) j = ne[j];   // 这里的j > 0, 如果不满足相等， 就需要跳
        if(p[i] == p[j + 1] )   j++;
        ne[i] = j;
    }
    
    // 匹配过程
    for(int i= 1,j = 0; i<=m; i++)
    {
        // 表示j 没有退回起点， 如果s的i个位置和p的j+1位置不匹配 ，直接进行ne数组调到指定位置
        while(j && s[i] != p[j + 1]) j = ne[j];
        if(s[i] == p[j+1] ) j++;
        if(j == n)
        {
            // 匹配成功
            printf("%d ", i - n);//我们按照坐标从1开始的，但题目中的是从0开始的， 这里有一个减1 和+1 相抵消
            j = ne[j];   // 输出所有可能匹配的位置， 所以匹配好了需要继续向右比较
        }
    }

    return 0;
}

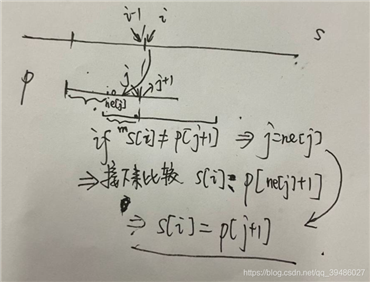
代码中的 s[i] != p[j + 1] 后的转移思路。

几大排序算法的理解和代码实现（超级详细的过程）

原文：https://www.cnblogs.com/acep/p/14021813.html