在之前关于数据结构的博客中已经介绍过两种最基础的数据结构:基于连续内存空间的向量(线性表)和基于链式节点结构的链表。
有序的向量可以通过二分查找以logn对数复杂度完成随机查找,但由于插入/删除元素时可能导致内部数组内整体数据的平移复制,导致随机插入/删除的效率较低。而普通的一维链表结构虽然可以做到高效的插入/删除元素(只是关联的节点拓扑结构改变),但是在随机查找时却效率较低,因为其只能从头/尾节点顺序的进行遍历才能找到对应节点。
计算机科学家发明了能够兼具向量与链表优点的平衡二叉搜索树(Balance Binary Search Tree BBST),这其中红黑树是平均性能最高,也最复杂的一种BBST。
正是因为高性能的平衡二叉树过于复杂,使得计算机科学家另辟蹊径,发明了被称为跳表(Skip List)的数据结构。跳表通过建立具有层次结构的索引节点,解决了普通链表无法进行二分查找的缺陷。跳表是基于链表的,因此其插入和删除效率和链表一样优秀;而由于索引节点的引入,也使得跳表可以以类似二分查找的形式进行特定元素的搜索,其查找性能也达到了O(logn)的对数复杂度,和有序向量以及平衡二叉树查询渐进时间复杂度一致。
总的来说,跳表是一个平均性能很优秀,结构相对简单的数据结构,在redis以及LevelDB、RocksDB等KV键值对数据库中被广泛使用。
跳表是一个拥有多层索引节点的链表,最低层是一个链表,保存着全部的原始数据节点。而索引节点是建立在最底层链表节点之上的,且从下到上索引节点的数量逐渐稀疏。
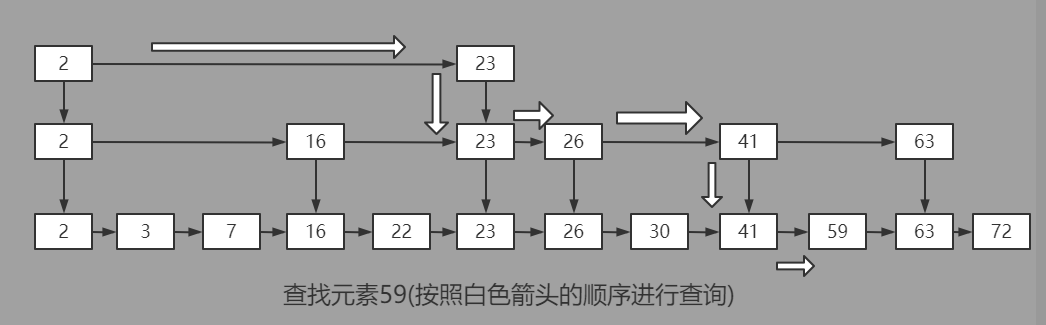
在查询时,从最高层开始以类似二分查找的方式跳跃着的逐步向下层逼近查找最终的目标节点。
跳表结构示意图:
了解了跳表的结构,以及其能够高效随机查询的原理之后。很自然的会想到一个问题,跳表的索引节点是如何维护的?换句话说,当插入/删除节点时跳表的索引结构是如何变化的?
要想保证跳表高效的查询效率,需要令跳表相邻的上下层节点的数量之比大致为1:2,且同一层索引节点的分布尽量均匀(二分查找)。
一种自然的想法是每次插入新节点时,详细的检查每一层的索引节点,精心维护相邻水平层索引节点1:2的数量,并控制节点排布的稀疏程度(必要时甚至可以重建整个索引)。但这样使得跳表的插入性能大大降低,所以实际上跳表并没有选择这种容易想到但低效方式维护索引。
在跳表中,通过类似丢硬币的方式,以概率来决定索引节点是否需要被创建。具体的说,每当插入一个新节点时,根据某种概率算法计算是否需要为其建立上一层的索引节点。如果判断需要建立,那么再接着进行一次基于概率的判断,如果为真则在更高一层也建立索引节点,并循环往复。
假设概率算法为真的数学期望为1/2,则插入新节点时有50%(1/2)的概率建立第一层的索引节点,25%(1/2^2)的概率建立第两层的索引节点,12.5%(1/2^3)的概率建立第三层的索引节点,以此类推。这种基于概率的索引节点建立方式,从宏观的数学期望上也能保证相邻上下层d的索引节点个数之比为1:2。同时由于插入节点数值的大小和插入顺序都是完全随机的,因此从期望上来说,同一水平层索引节点的分布也是大致均匀的。
总的来说,插入新节点时基于概率的索引建立算法插入效率相对来说非常高,虽然在极端情况下会导致索引节点上下、水平的分布不均,但依然是非常优秀的实现。同时,可以通过控制概率算法的数学期望,灵活的调整跳表的空间占用与查询效率的取舍(概率算法为真的数学期望从1/2降低到1/4时,建立上级索引的概率降低,索引的密度下降,因此其随机查询效率降低,但其索引节点将会大大减少以节约空间,跳表的这一特性在对空间占用敏感的内存数据库应用中是很有价值的)。
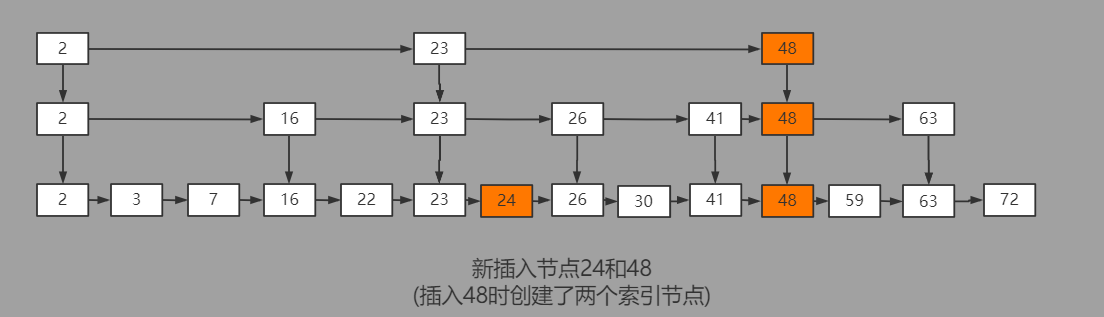
跳表插入节点示意图:
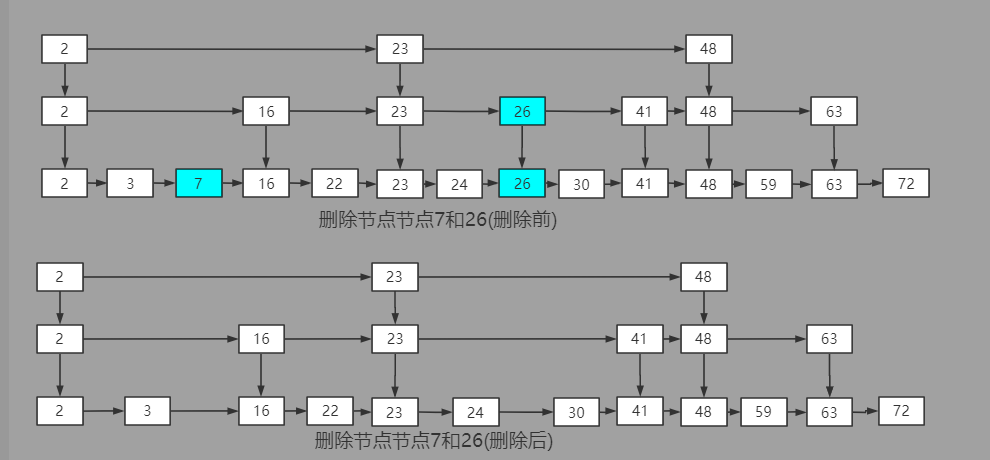
在理解了跳表插入的原理后,跳表的删除就很好理解了。当最底层的数据节点被删除时,只需要将其之上的所有索引节点一并删除即可。
跳表删除节点示意图:
下面介绍跳表的实现细节。本篇博客的跳表SkipListMap是用java实现的,为了令代码更容易理解,在一些地方选择了效率相对较低,但更容易理解的实现。
为了令整个跳表的实现更加简单,局别与jdk的ConcurrentSkipListMap。当前版本跳表的定义的节点结构既用于最底层的数据节点,也用于上层的索引节点;且节点持有上、下、左、右关联的四个节点的引用。在每一水平层引入了左右两个哨兵节点,通过节点中的NodeType枚举区分哨兵节点与普通的索引/数据节点。
为了能够在后续介绍的插入/删除等操作中,更加简单的定位到临近的节点,简化代码的理解难度。相比jdk、redis等工程化的高性能跳表实现,当前版本实现的跳表节点冗余了一些不必要的字段属性以及额外的哨兵节点,额外的浪费了一些空间,但跳表实现的核心思路是一致的。
跳表Node节点定义:
private static class Node<K,V> implements EntryNode<K,V>{ K key; V value; Node<K,V> left; Node<K,V> right; Node<K,V> up; Node<K,V> down; NodeType nodeType; private Node(K key,V value) { this.key = key; this.value = value; this.nodeType = NodeType.NORMAL; } private Node() { } private Node(NodeType nodeType) { this.nodeType = nodeType; } /** * 将一个节点作为"当前节点"的"右节点" 插入链表 * @param node 需要插入的节点 * */ private void linkAsRight(Node<K,V> node){ // 先设置新增节点的 左右节点 node.left = this; node.right = this.right; // 将新增节点插入 当前节点和当前节点的左节点之间 this.right.left = node; this.right = node; } /** * 将"当前节点"从当前水平链表移除(令其左右节点直接牵手) * */ private void unlinkSelfHorizontal(){ // 令当前链表的 左节点和右节点建立关联 this.left.right = this.right; // 令当前链表的 右节点和左节点建立关联 this.right.left = this.left; } /** * 将"当前节点"从当前垂直链表移除(令其上下节点直接牵手) * */ private void unlinkSelfVertical(){ // 令当前链表的 左节点和右节点建立关联 this.up.down = this.down; // 令当前链表的 右节点和左节点建立关联 this.down.up = this.up; } @Override public String toString() { if(this.key != null){ return "{" + "key=" + key + ",value=" + value + ‘}‘; }else{ return "{" + "nodeType=" + nodeType + ‘}‘; } } @Override public K getKey() { return this.key; } @Override public V getValue() { return this.value; } @Override public void setValue(V value) { this.value = value; } }
NodeType枚举:
private enum NodeType{ /** * 普通节点 * */ NORMAL, /** * 左侧哨兵节点 * */ LEFT_SENTINEL, /** * 右侧哨兵节点 * */ RIGHT_SENTINEL, ; }
跳表是一个能够支持高效增删改查、平均性能很高的数据结构,对标的是红黑树为首的平衡二叉搜索树。因此在我们参考jdk的实现,跳表和之前系列博客中的TreeMap一样也实现了Map接口。
跳表的每一个水平层是从左到右,有小到大进行排序的,具体的比较逻辑由compare函数来完成。
跳表定义:
public class SkipListMap<K,V> extends AbstractMap<K,V>{ private Node<K,V> head; private Node<K,V> tail; private Comparator<K> comparator; private int maxLevel; private int size; /** * 插入新节点时,提升的概率为0.5,期望保证上一层和下一层元素的个数之比为 1:2 * 以达到查询节点时,log(n)的对数时间复杂度 * */ private static final double PROMOTE_RATE = 1.0/2.0; private static final int INIT_MAX_LEVEL = 1; public SkipListMap() { // 初始化整个跳表结构 initialize(); } public SkipListMap(Comparator<K> comparator) { this(); // 设置比较器 this.comparator = comparator; } private void initialize(){ this.size = 0; this.maxLevel = INIT_MAX_LEVEL; // 构造左右哨兵节点 Node<K,V> headNode = new Node<>(); headNode.nodeType = NodeType.LEFT_SENTINEL; Node<K,V> tailNode = new Node<>(); tailNode.nodeType = NodeType.RIGHT_SENTINEL; // 跳表初始化时只有一层,包含左右哨兵两个节点 this.head = headNode; this.tail = tailNode; // 左右哨兵牵手 this.head.right = this.tail; this.tail.left = this.head; } 。。。。。。 }
compare比较逻辑实现:
private int doCompare(K key1,K key2){ if(this.comparator != null){ // 如果跳表被设置了比较器,则使用比较器进行比较 return this.comparator.compare(key1,key2); }else{ // 否则强制转换为Comparable比较(对于没有实现Comparable的key会抛出强制类型转换异常) return ((Comparable)key1).compareTo(key2); } }
跳表实现的一个关键就是如何进行快速的随机查找。
对于指定key的查找,首先从最上层的跳表head节点开始,从左到右的进行比对,当找到一个节点比key小,而且其相邻的右节点比key大时,则沿着找到的节点进入下一层继续查找。(每一个水平层的左哨兵节点视为无穷小,而右哨兵节点视为无穷大)
由于跳表的相邻上下两层的节点稀疏程度不同,进入下一水平层更有可能逼近指定key对应的数据节点。通过在水平层大跨步的跳跃,并在对应的节点处进入下一层,循环往复的如此操作直到最底层。跳跃式的进行链表节点的查找方式,也是跳表名称SkipList的来源。
从代码实现中可以看到,跳表通过建立在其上的索引节点进行查找,比起原始的一维链表,能够更快的定位到所要查找的节点。且如果按照概率算法构建的索引节点分布比较平均的话,跳表的查找效率将能够媲美有序向量、平衡二叉树的查找效率。
跳表查找方法实现:
/** * 找到最逼近参数key的前驱数据节点 * (返回的节点的key并不一定等于参数key,也有可能是最逼近的) * */ private Node<K,V> findPredecessorNode(K key){ // 从跳表头结点开始,从上层到下层逐步逼近 Node<K,V> currentNode = head; while(true){ // 当前遍历节点的右节点不是右哨兵,且data >= 右节点data while (currentNode.right.nodeType != NodeType.RIGHT_SENTINEL && doCompare(key,currentNode.right.key) >= 0){ // 指向同一层的右节点 currentNode = currentNode.right; } // 跳出了上面循环,说明找到了同层最接近的一个节点 if(currentNode.down != null){ // currentNode.down != null,未到最底层,进入下一层中继续查找、逼近 currentNode = currentNode.down; }else{ // currentNode.down == null,说明到了最下层保留实际节点的,直接返回 // (currentNode.key并不一定等于参数key,可能是最逼近的前缀节点) return currentNode; } } } /** * 找到key对应的数据节点 * 如果没有找到,返回null * */ private Node<K,V> searchNode(K key){ Node<K,V> preNode = findPredecessorNode(key); if(preNode.key != null && Objects.equals(preNode.key,key)){ return preNode; }else{ return null; } }
跳表在插入节点的过程中,首先通过findProdecessorNode查询到最逼近key的前驱数据节点,如果发现当前key并不存在,则在最底层的数据节点链表中插入新的数据节点。
在新的数据节点插入完成后,根据random生成一个0-1之间的随机数,与定义的PROMOTE_RATE常量进行比对,判断是否需要为当前新插入的节点创建更上一层的索引节点。这一比对可能会进行多次,相对应的也会为新插入节点在垂直方向上创建更多的索引节点。
跳表插入代码:
private Node<K,V> putNode(K key,V value){ if(key == null){ throw new RuntimeException("key required"); } // 从最底层中,找到其直接最接近的前驱节点 Node<K,V> predecessorNode = findPredecessorNode(key); if(Objects.equals(key,predecessorNode.key)){ // data匹配,已经存在,直接返回false代表未插入成功 return predecessorNode; } // 当前跳表元素个数+1 this.size++; // 之前不存在,需要新插入节点 Node<K,V> newNode = new Node<>(key,value); // 将新节点挂载至前驱节点之后 predecessorNode.linkAsRight(newNode); int currentLevel = INIT_MAX_LEVEL; Random random = new Random(); Node<K,V> hasUpNodePredecessorNode = predecessorNode; Node<K,V> newNodeUpperNode = newNode; boolean doPromoteLevel = false; while (random.nextDouble() < PROMOTE_RATE && !doPromoteLevel) { // 当前插入的节点需要提升等级,在更高层插入索引节点 if(currentLevel == this.maxLevel){ promoteLevel(); // 保证一次插入节点,做多只会提升一层(否则将会有小概率出现高位的许多层中只有极少数(甚至只有1个)元素的情况) doPromoteLevel = true; } // 找到上一层的前置节点 while (hasUpNodePredecessorNode.up == null) { // 向左查询,直到找到最近的一个有上层节点的前驱节点 hasUpNodePredecessorNode = hasUpNodePredecessorNode.left; } // 指向上一层的node hasUpNodePredecessorNode = hasUpNodePredecessorNode.up; Node<K,V> upperNode = new Node<>(key,value); // 将当前data的up节点和上一层最接近的左上的node建立连接 hasUpNodePredecessorNode.linkAsRight(upperNode); // 当前data这一列的上下节点建立关联 upperNode.down = newNodeUpperNode; newNodeUpperNode.up = upperNode; // 由于当前data节点可能需要在更上一层建立索引节点,所以令newNodeUpperNode指向更上层的up节点 newNodeUpperNode = newNodeUpperNode.up; // 当前迭代层次++ currentLevel++; } return null; }
在通过概率算法决定是否建立更高层索引节点的过程中,有可能需要额外的再升高一层。这时需要通过promoteLevel方法将整个跳表的水平层抬高一层,并令跳表的head作为新增水平层的左哨兵节点。
promoteLevel方法实现:
/** * 提升当前跳表的层次(在当前最高层上建立一个只包含左右哨兵的一层,并令跳表的head指向左哨兵) * */ private void promoteLevel(){ // 最大层数+1 this.maxLevel++; // 当前最高曾左、右哨兵节点 Node<K,V> upperLeftSentinel = new Node<>(NodeType.LEFT_SENTINEL); Node<K,V> upperRightSentinel = new Node<>(NodeType.RIGHT_SENTINEL); // 最高层左右哨兵牵手 upperLeftSentinel.right = upperRightSentinel; upperRightSentinel.left = upperLeftSentinel; // 最高层的左右哨兵,和当前第一层的head/right建立上下连接 upperLeftSentinel.down = this.head; upperRightSentinel.down = this.tail; this.head.up = upperLeftSentinel; this.tail.up = upperRightSentinel; // 令跳表的head/tail指向最高层的左右哨兵 this.head = upperLeftSentinel; this.tail = upperRightSentinel; }
跳表的删除相对简单,在找到需要被删除的最底层数据节点之后,通过up引用找到其对应的所有索引节点删除即可。
当删除某一索引节点后,如果发现对应水平层只剩下左/右哨兵时,还需要通过destoryLevel方法将对应的水平层删除。
跳表删除节点:
private Node<K,V> removeNode(Node<K,V> needRemoveNode){ if (needRemoveNode == null){ // 如果没有找到对应的节点,不需要删除,直接返回 return null; } // 当前跳表元素个数-1 this.size--; // 保留需要返回的最底层节点Node Node<K,V> returnCache = needRemoveNode; // 找到了对应节点,则当前节点以及其所有层的up节点都需要被删除 int currentLevel = INIT_MAX_LEVEL; while (needRemoveNode != null){ // 将当前节点从该水平层的链表中移除(令其左右节点直接牵手) needRemoveNode.unlinkSelfHorizontal(); // 当该节点的左右都是哨兵节点时,说明当前层只剩一个普通节点 boolean onlyOneNormalData = needRemoveNode.left.nodeType == NodeType.LEFT_SENTINEL && needRemoveNode.right.nodeType == NodeType.RIGHT_SENTINEL; boolean isLowestLevel = currentLevel == INIT_MAX_LEVEL; if(!isLowestLevel && onlyOneNormalData){ // 不是最底层,且只剩当前一个普通节点了,需要删掉这一层(将该层的左哨兵节点传入) destroyLevel(needRemoveNode.left); }else{ // 不需要删除该节点 currentLevel++; } // 指向该节点的上一点 needRemoveNode = needRemoveNode.up; } return returnCache; }
跳表删除水平层destoryLevel实现:
private void destroyLevel(Node<K,V> levelLeftSentinelNode){ // 最大层数减1 this.maxLevel--; // 当前层的右哨兵节点 Node<K,V> levelRightSentinelNode = levelLeftSentinelNode.right; if(levelLeftSentinelNode == this.head){ // 需要删除的是当前最高层(levelLeftSentinelNode是跳表的头结点) // 令下一层的左右哨兵节点的up节点清空 levelLeftSentinelNode.down.up = null; levelRightSentinelNode.down.up = null; // 令跳表的head/tail指向最高层的左右哨兵 this.head = levelLeftSentinelNode.down; this.tail = levelRightSentinelNode.down; }else{ // 需要删除的是中间层 // 移除当前水平层左哨兵,令其上下节点建立连接 levelLeftSentinelNode.unlinkSelfVertical(); // 移除当前水平层右哨兵,令其上下节点建立连接 levelRightSentinelNode.unlinkSelfHorizontal(); } }
高效的跳表实现(例如jdk的ConcurrentSkipListMap)相对于本篇博客的简易版实现,上层的索引节点只需要持有down和right两个关联节点的引用即可(K/V引用也可以简化为对底层数据节点的引用),而最底层的数据节点则仅维护关联的right节点即可。同时,通过边界条件的判断,也并不需要水平层的左右哨兵节点。
可以看到,高效跳表的空间效率其实很高,其空间占用正比于数据节点的数目,渐进的空间复杂度为O(n)。在redis的zset实现中,就是使用跳表作为其底层实现的。redis的zset跳表实现中,建立上一级索引节点的概率被设置为1/4,综合来看每个节点所持有的平均引用数量大约为1.33,比红黑树节点2个引用(左右孩子节点,都不考虑value的引用)的空间效率要高。
跳表通过概率算法建立起了均匀分布的索引节点层(从数学期望上来看是均匀分布的,但存在一定波动),能够以正比于跳表层数的O(logn)对数时间复杂度完成随机查询。
跳表的查询操作效率与跳表的层数有关,因此跳表查询操作的渐进时间复杂度为O(logn)。
跳表和哈希表在对空间/时间的取舍上类似,哈希表可以通过调整负载因子进行空间效率与查询时间效率的取舍;而跳表也可以通过设置增加上一层索引节点的概率来调节查询效率与空间效率。
跳表的插入依赖于跳表的查询(logn),且需要根据概率决定是否创建对应的上一层索引节点。在最坏情况下,可能需要创建n+1个索引节点(n为跳表当前层数,1表示可能会增加新的一层);最好情况下不需要创建任何索引节点。
跳表的插入操作效率与跳表的层数有关,因此跳表插入操作的渐进时间复杂度为O(logn)。
跳表的删除同样依赖于跳表的查询,删除最底层数据节点时也需要将被删除节点对应的索引节点一并删除。在最坏情况下,可能需要删除至多n个索引节点(n为跳表层数),最好情况下不需要删除任何索引节点。
跳表的删除操作效率与跳表的层数有关,因此跳表删除操作的渐进时间复杂度为O(logn)。
下面是redis作者给出的回答:
1) They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.
2) A sorted set is often target of many ZRANGE or ZREVRANGE operations, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.
3) They are simpler to implement, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.
大致的翻译:
1) 跳表是否很消耗内存,这取决于你。通过改变提升跳表节点索引等级的概率参数可以令跳表的内存消耗少于B树。
2) 一个有序集合通常被作为ZRANGE或是ZREVERANGE操作的目标。也就是说,通常是以链表的形式来遍历跳表的,在这种遍历操作下,缓存了相邻节点位置的跳表性能将至少和其它类型的自平衡树一样优秀。
3) 跳表更容易实现和调试,等等。得益于跳表的简单性,我收到了一个能够在跳表中以O(logN)效率实现ZRANK的补丁(已经在redis的master分支中了),而这只需要对代码稍作修改。
经过前面博客中对跳表原理的介绍,是否对redis作者的回答有了更深的体会呢?
通过自己的思路实现了一个简易版的跳表之后,理解了跳表的设计思想,也使得我有能力更进一步的去理解jdk、redis中更为高效的跳表实现。同时也加深了对跳表、平衡二叉树、哈希表等不同数据结构的理解,以及如何在不同场景下应该如何选择更高效、更符合实际需求的数据结构。
本系列博客的代码在我的 github上:https://github.com/1399852153/DataStructures (SkipListMap类),存在许多不足之处,还请多多指教。
原文:https://www.cnblogs.com/xiaoxiongcanguan/p/14032756.html