首页 > 编程语言 > 详细

KNN的改进算法、剪辑近邻法与压缩近邻法的MATLAB实现

时间：2020-11-27 22:26:41      阅读：36      评论：0      收藏：0      [点我收藏+]

KNN（K - Nearest Neighbor）分类算法是模式识别领域的一个简单分类方法。KNN算法的核心思想是，如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的k个样本的类别来决定待分样本所属的类别。

首先，knn算法比较适合只有两类样本的简单分类问题，这样当n为奇数时就可以少数服从多数达到分类目的。但是当类别数量大于2时，设定n为奇数已经不能避免投票数量相同的问题。这种情况在我的理解下有两种解决思路：

思路A：当对运算效率要求较高而对分类结果要求不高时，可以选择投票数量相同的样本类别中先被查询到的一个；

思路B：当对运算效率要求不高而对分类结果要求较高时，可以改变k值再次进行投票，例如，在k0=5时出现了投票数量相同的样本类别，可以令k1=k0-1再次进行判断，若仍存在投票数量相同的样本类别，可以继续令k2=k1-1再次进行判断，这样在km=1时会得到唯一答案。这里不建议增大k值再次投票，因为我担心会陷入更麻烦的情况。

KNN作为机器学习的入门算法，存在效率低、过度依赖训练数据的缺点，并在处理较大数据时可能引起维数灾难。需要谨慎考虑后再选择。

在普通的KNN算法下，当k个最近邻样本进行投票时，存在投票数量相同的样本类别，即MaxValue的长度不为1时程序会报错。根据思路A，可将MaxValue改为MaxValue(1)。下面的算法在这里根据思路B进行改进，具体方法是减小k值递归调用knn函数。

同时为了满足压缩近邻法的需要，处理了当训练集数据不足K个时出现的问题。解决方法是，当训练集数据不足K个时，令K为训练集数据的个数。

改进后的KNN算法：

function y = knn(trainData, sample_label, testData, k)

%KNN k-Nearest Neighbors Algorithm.
%
%   INPUT:  trainData:       training sample Data, M-by-N matrix.
%           sample_label:    training sample labels, 1-by-N row vector.
%           testData:        testing sample Data, M-by-N_test matrix.
%           K:               the k in k-Nearest Neighbors
%
%   OUTPUT: y    : predicted labels, 1-by-N_test row vector.
%
% Author: Sophia_Dz

if length(trainData) < k
    k = length(trainData);
end
 
[M_train, N] = size(trainData);
[M_test, ~] = size(testData);
 
%calculate the distance between testData and trainData

Dis = zeros(M_train,1);
class_test = zeros(M_test,1);
for n = 1:M_test
    for i = 1:M_train
        distance1 = 0;
        for j = 1:N
            distance1 = (testData(n,j) - trainData(i,j)).^2 + distance1;
        end
        Dis(i,1) = distance1.^0.5;
    end
    %find the k nearest neighbor
    [~, index] = sort(Dis);
    temp=1:k;
    for i = 1:k
        temp(i) = sample_label(index(i));
    end
    table = tabulate(temp);
    MaxCount=max(table(:,2,:));
    [row,~]=find(table(:,2,:)==MaxCount);
    MaxValue=table(row,1);
    if length(MaxValue) ~= 1
        MaxValue = knn(trainData, sample_label, testData(n,:), k-1);
    end
    class_test(n) = MaxValue;
end
y = class_test;

下面是剪辑近邻法与压缩近邻法的MATLAB实现：

首先设定参数：

%% parameter determination
clear;
% dataset parameter
dataset_len=400;
dataset_proportion=[8,2];
attribute_num=2;
% knn parameter
k=5;
% edit parameter
m=4;
s=4;

准备数据，这里使用MATLAB生成服从正态分布的三组数据，它们的均值不同：

%% dataset load
dataset_class_len=fix(dataset_len/3);
dataset=[
    4*ones(dataset_class_len,1)+randn(dataset_class_len,1),... % class A attribute x
    2*ones(dataset_class_len,1)+randn(dataset_class_len,1),... % class A attribute y
    1*ones(dataset_class_len,1);                               % class A label
    2*ones(dataset_class_len,1)+randn(dataset_class_len,1),... % class B attribute x
    4*ones(dataset_class_len,1)+randn(dataset_class_len,1),... % class B attribute y
    2*ones(dataset_class_len,1);                               % class B label
    5*ones(dataset_class_len,1)+randn(dataset_class_len,1),... % class C attribute x
    5*ones(dataset_class_len,1)+randn(dataset_class_len,1),... % class C attribute y
    3*ones(dataset_class_len,1)                                % class C label
    ];

将数据划分为训练集与测试集：

%% preprocess data
% order disrupt
rand_class_index=randperm(size(dataset,1));
dataset=dataset(rand_class_index,:);
% train dataset and test dataset
dataset_train_len=fix(dataset_len*(dataset_proportion(1)/sum(dataset_proportion)));
dataset_train=dataset(1:dataset_train_len,:);
dataset_test=dataset(dataset_train_len+1:end,:);
% attribute and label
dataset_train_attribute=dataset_train(:,1:attribute_num);
dataset_train_label=dataset_train(:,attribute_num+1);
dataset_test_attribute=dataset_test(:,1:attribute_num);
dataset_test_label=dataset_test(:,attribute_num+1);

将训练集的样本可视化：

%% train dataset visualization
data_vis=dataset_train;
figure(1);
for n=1:length(data_vis)
    X=data_vis(n,1);
    Y=data_vis(n,2);
    if data_vis(n,attribute_num+1)==1
        color=‘red‘;
    elseif data_vis(n,attribute_num+1)==2
        color=‘green‘;
    elseif data_vis(n,attribute_num+1)==3
        color=‘blue‘;
    end
    plot(X,Y,‘+‘,‘Color‘,color);
    hold on;
end

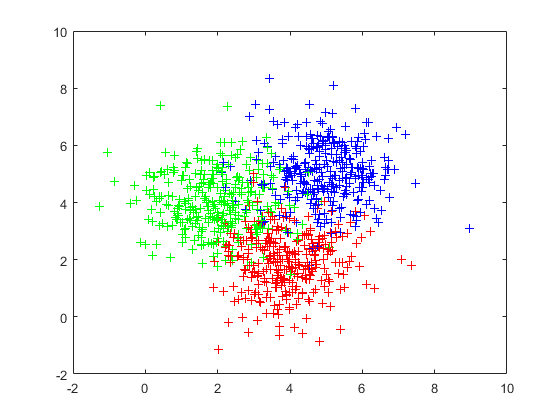
技术分享图片

图1 未经处理的训练集样本

分类：

%% knn
classification_result=knn(dataset_train_attribute,dataset_train_label,dataset_test_attribute,k);

计算根据此训练集的分类正确率为：0.8481：

%% correct rate
error_count=0;
for n=1:length(classification_result)
    if dataset_test_label(n)~=classification_result(n)
        error_count=error_count+1;
    end
end
correct_rate=1-error_count/length(classification_result);

剪辑近邻法：

剪辑近邻法的基本思想是，当不同类别的样本在分布上有交迭部分的，分类的错误率主要来自处于交迭区中的样本，通过剪辑去除大部分交迭区中的样本。

1. 将训练集随机划分成s组；

2. 其中i组作为训练集，i+1组样本作为测试集，用训练集中的样本对测试集中的样本进行最近邻分类，如果类别不同，则从测试集中分类错误的样本去除；

3. 若达到m次没有新的样本被去除，剪辑完成。

%% edit nearest neighbor
% init
dataset_edit=dataset_train;
loop=0;
add_old=1;
while loop<m
    rand_class_index=ceil(unifrnd(0,s,length(dataset_edit),1));
    dataset_new=zeros(length(dataset_edit),attribute_num+1);
    add=1;
    for i=1:s
        % train set and test set
        test_set=dataset_edit((rand_class_index==i),:);
        if i<s
            j=i+1;
        else
            j=1;
        end
        train_set=dataset_edit((rand_class_index==j),:);
        train_set_attribute=train_set(:,1:attribute_num);
        train_set_label=train_set(:,attribute_num+1);
        test_set_attribute=test_set(:,1:attribute_num);
        test_set_label=test_set(:,attribute_num+1);
        % classification
        result=knn(train_set_attribute,train_set_label,test_set_attribute,k);
        for num=1:length(result)
            if(result(num)==test_set_label(num))
                dataset_new(add,:)=test_set(num,:);
                add=add+1;
            end
        end
    end
    dataset_edit=dataset_new(1:add-1,:);
    if(add==add_old)
        loop=loop+1;
    end
    add_old=add;
end

剪辑后的训练集：

%% edit data visualization
data_vis=dataset_edit;
figure(2);
for n=1:length(data_vis)
    X=data_vis(n,1);
    Y=data_vis(n,2);
    if data_vis(n,attribute_num+1)==1
        color=‘red‘;
    elseif data_vis(n,attribute_num+1)==2
        color=‘green‘;
    elseif data_vis(n,attribute_num+1)==3
        color=‘blue‘;
    end
    plot(X,Y,‘+‘,‘Color‘,color);
    hold on;
end

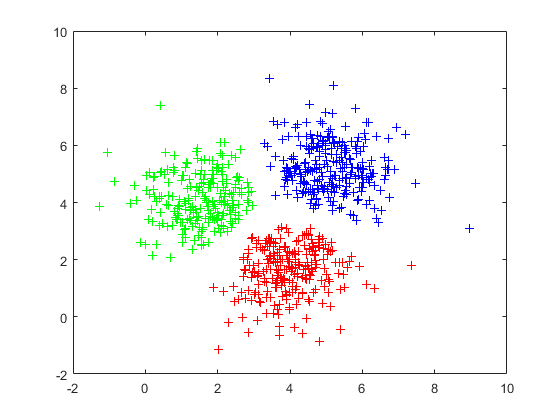
技术分享图片

图2 剪辑处理的训练集样本

分类：

%% edit knn
dataset_edit_attribute=dataset_edit(:,1:attribute_num);
dataset_edit_label=dataset_edit(:,attribute_num+1);
classification_result_edit=knn(dataset_edit_attribute,dataset_edit_label,dataset_test_attribute,k);

计算根据此训练集的分类正确率为：0.8734：

%% edit correct rate
error_count=0;
for n=1:length(classification_result_edit)
    if dataset_test_label(n)~=classification_result_edit(n)
        error_count=error_count+1;
    end
end
correct_rate_edit=1-error_count/length(classification_result_edit);

压缩近邻法：

压缩近邻法压缩样本的思想，它利用现有样本集，逐渐生成一个新的样本集。使该样本集在保留最少量样本的条件下, 仍能对原有样本的全部用最近邻法正确分类，那么该样本集也就能对待识别样本进行分类, 并保持正常识别率。

1. 对初始训练集，将其划分为两个部分Store和Garbbag，初始Store样本集合为空。

2. 从初始训练集中随机选择一个样本放入Store中，其它样本放入Garbbag中，用其对Garbbag中的每一个样本进行分类。若样本i能够被正确分类，则将其放回到Garbbag中；否则将其加入到Store中；

3. 重复上述过程，直到Garbbag中所有样本都能正确分类为止。

%% condense nearest neighbor
% init
dataset_condense=dataset_train;
store=zeros(size(dataset_condense));
store_count=0;
garbbag=dataset_condense;
garbbag_count=length(dataset_condense);
add=garbbag_count;
% move one
store(store_count+1,:)=garbbag(add,:);
garbbag(add,:)=[];
store_count=store_count+1;
garbbag_count=garbbag_count-1;
add=add-1;
store_attribute=store(:,1:attribute_num);
store_label=store(:,attribute_num+1);
garbbag_attribute=garbbag(:,1:attribute_num);
garbbag_label=garbbag(:,attribute_num+1);
change_flag=1;
while change_flag==1
    change_flag=0;
    add=garbbag_count;
    while add>0
        result=knn(store_attribute,store_label,garbbag_attribute(add,:),k);
        if result~=garbbag_label(add)
            change_flag=1;
            store(store_count+1,:)=garbbag(add,:);
            garbbag(add,:)=[];
            store_count=store_count+1;
            garbbag_count=garbbag_count-1;
            add=add-1;
            store_attribute=store(:,1:attribute_num);
            store_label=store(:,attribute_num+1);
            garbbag_attribute=garbbag(:,1:attribute_num);
            garbbag_label=garbbag(:,attribute_num+1);
        end
        add=add-1;
    end
end
dataset_condense=store;

压缩后的训练集：

%% condense data visualization
data_vis=dataset_condense;
figure(3);
for n=1:length(data_vis)
    X=data_vis(n,1);
    Y=data_vis(n,2);
    if data_vis(n,attribute_num+1)==1
        color=‘red‘;
    elseif data_vis(n,attribute_num+1)==2
        color=‘green‘;
    elseif data_vis(n,attribute_num+1)==3
        color=‘blue‘;
    end
    plot(X,Y,‘+‘,‘Color‘,color);
    hold on;
end

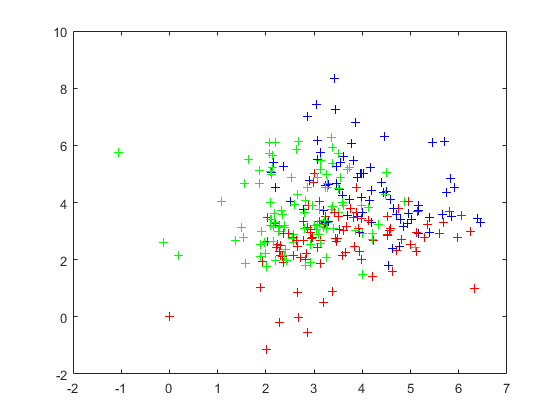
技术分享图片

图3 压缩处理的训练集样本

分类：

%% condense knn
dataset_condense_attribute=dataset_condense(:,1:attribute_num);
dataset_condense_label=dataset_condense(:,attribute_num+1);
classification_result_condense=knn(dataset_condense_attribute,dataset_condense_label,dataset_test_attribute,k);

计算根据此训练集的分类正确率为：0.8228：

%% condense correct rate
error_count=0;
for n=1:length(classification_result_condense)
    if dataset_test_label(n)~=classification_result_condense(n)
        error_count=error_count+1;
    end
end
correct_rate_condense=1-error_count/length(classification_result_condense);

将剪辑后的样本压缩处理：

%% edit and condense nearest neighbor
% init
dataset_ec=dataset_edit;
store=zeros(size(dataset_ec));
store_count=0;
garbbag=dataset_ec;
garbbag_count=length(dataset_ec);
add=garbbag_count;
% move one
store(store_count+1,:)=garbbag(add,:);
garbbag(add,:)=[];
store_count=store_count+1;
garbbag_count=garbbag_count-1;
add=add-1;
store_attribute=store(:,1:attribute_num);
store_label=store(:,attribute_num+1);
garbbag_attribute=garbbag(:,1:attribute_num);
garbbag_label=garbbag(:,attribute_num+1);
change_flag=1;
while change_flag==1
    change_flag=0;
    add=garbbag_count;
    while add>0
        result=knn(store_attribute,store_label,garbbag_attribute(add,:),k);
        if result~=garbbag_label(add)
            change_flag=1;
            store(store_count+1,:)=garbbag(add,:);
            garbbag(add,:)=[];
            store_count=store_count+1;
            garbbag_count=garbbag_count-1;
            add=add-1;
            store_attribute=store(:,1:attribute_num);
            store_label=store(:,attribute_num+1);
            garbbag_attribute=garbbag(:,1:attribute_num);
            garbbag_label=garbbag(:,attribute_num+1);
        end
        add=add-1;
    end
end
dataset_ec=store;

压缩处理剪辑后的样本：

%% edit and condense data visualization
data_vis=dataset_ec;
figure(4);
for n=1:length(data_vis)
    X=data_vis(n,1);
    Y=data_vis(n,2);
    if data_vis(n,attribute_num+1)==1
        color=‘red‘;
    elseif data_vis(n,attribute_num+1)==2
        color=‘green‘;
    elseif data_vis(n,attribute_num+1)==3
        color=‘blue‘;
    end
    plot(X,Y,‘+‘,‘Color‘,color);
    hold on;
end

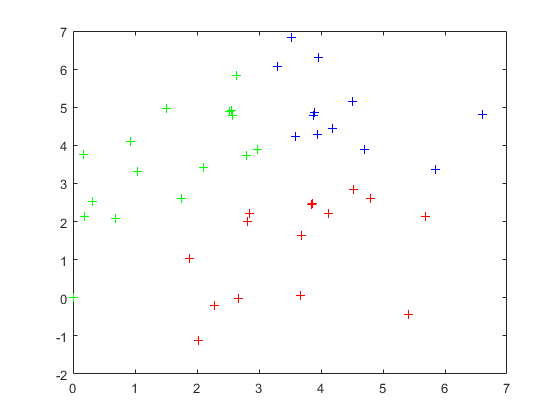
技术分享图片

图4 剪辑压缩处理的训练集样本

分类：

%% edit and condense knn
dataset_ec_attribute=dataset_ec(:,1:attribute_num);
dataset_ec_label=dataset_ec(:,attribute_num+1);
classification_result_ec=knn(dataset_ec_attribute,dataset_ec_label,dataset_test_attribute,k);

计算根据此训练集的分类正确率为：0.8228：

%% edit and condense correct rate
error_count=0;
for n=1:length(classification_result_ec)
    if dataset_test_label(n)~=classification_result_ec(n)
        error_count=error_count+1;
    end
end
correct_rate_ec=1-error_count/length(classification_result_ec);

经过多次实验得到以下结论：

1. 剪辑处理能够去除分类边界的样本；

2. 压缩近邻主要去除样本中靠近中心的样本；

3. 剪辑近邻法可以去除部分样本并在一定程度上提高分类正确率；

4. 压缩近邻法可以去除大量样本。

KNN的改进算法、剪辑近邻法与压缩近邻法的MATLAB实现

原文：https://www.cnblogs.com/stephen0829/p/14049849.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
分享档案
更多>
2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)
最新文章
更多>
教程昨日排行
更多>
友情链接
汇智网   PHP教程   插件网  
关于我们 - 联系我们 - 留言反馈 - 联系我们:wmxa8@hotmail.com
© 2014 bubuko.com 版权所有
打开技术之扣，分享程序人生！