在计算科学中有一个著名的例子,斐波那契数列(fabnacci)序列,它是考察我们递归思想的运用。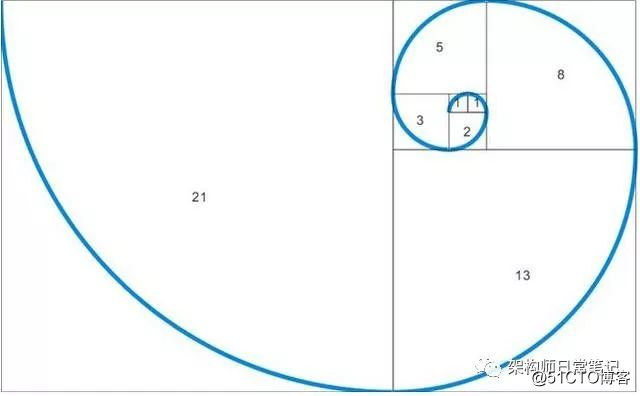
我们简单描述一下,F(n)满足下面的条件:
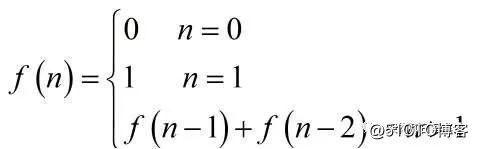
当n=0时F(n)=0
当n=1时F(n)=1
当n>1时,F(n)=F(n-1)+F(n-2).
示例,F(n)的数组从0.....n
0,1,1,2,3,5,8,13,21,34,55,89,144,。。。。
那么如何实现呢?我们来看一下
1.两层递归
最简单的一种实现:
public static long fibonacci(int n){
if(n==0) return 0;
else if(n==1) return 1;
else
return fibonacci(n-1)+fibonacci(n-2);
}问题是:随着n的数值逐渐增多,时间和空间耗费太大,读者可以自行实验。在我的机器上n=50时就不能忍受了。
2.一层递归
考虑优化方式
public static void main(String[] args) {
long tmp=0;
// TODO Auto-generated method stub
int n=10;
Long start=System.currentTimeMillis();
for(int i=0;i<n;i++){
System.out.print(fibonacci(i)+" ");
}
System.out.println("-------------------------");
System.out.println("耗时:"+(System.currentTimeMillis()-start));
}
public static long fibonacci(int n) {
long result = 0;
if (n == 0) {
result = 0;
} else if (n == 1) {
result = 1;
tmp=result;
} else {
result = tmp+fibonacci(n - 2);
tmp=result;
}
return result;
}递归时间减少了到不到50%
3.不使用递归
最好的方式,不使用递归的方式来做。
public static long fibonacci(int n){
long before=0,behind=0;
long result=0;
for(int i=0;i<n;i++){
if(i==0){
result=0;
before=0;
behind=0;
}
else if(i==1){
result=1;
before=0;
behind=result;
}else{
result=before+behind;
before=behind;
behind=result;
}
}
return result;
}面试官可以通过这个题目考察:1.是否熟悉基本的递归实现,递归思想在计算机科学属于最基本的思想。2:是否有优化的思路,通过时间和空间复杂度的转换来减少递归的次数。3:最终是否实现无递归来大大提升运算效率。
面试中如何答好斐波那契数列fabnacci实现之java版?
原文:https://blog.51cto.com/15015181/2556411