给定一个包含n个整数的数组nums,判断nums中是否存在三个元素a,b,c,使得a+b+c=0,并找出所有满足条件且不重复的三元组。(注:不包含重复的三元组)。
例如,给定数组nums=[-1,0,1,2,-1,-4],则满足要求的三元组集合为:
[ [-1, 0, 1], [-1, -1, 2] ]
首先对数组进行排序,用于定位基准点。假设以排序后首个固定元素nums[i](i=0)为起始点,再以左指针指向nums[i+1](简略记为nums[l]),右指针指向nums[len-1](简略记为nums[r]),即指向nums[i]右侧元素的两端,计算三数之和是否满足条件为0。如不满足且和小于0,则L++;反之则R--,有序移动两端指针,当L与R碰撞时(L>=R)时本轮遍历结束,右移起始点(i++);如三数之和为0,满足条件则记录并继续移动两端指针。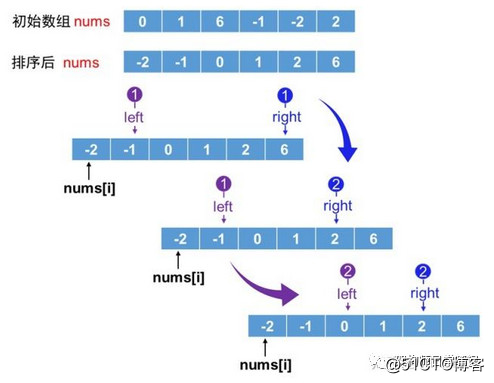
图1:引用自知乎的图解
由于按小到大排序,因此如果作为起始点的nums[i]>0,则三数之和必然无法等于0,此时可结束循环。如果nums[i]==nums[i?1],则说明该元素重复,根据题意需要跳过,避免输出重复的结果。
此外,当三数之和为0时,假设nums[L]==nums[L+1]会导致结果重复,需要跳过该元素(L++);如果nums[R]==nums[R?1]同样会导致结果重复,也需要跳过该元素(R--)。总体来说,时间复杂度为:O(n2)。
public static void sum3(int[] nums) {
if(nums != null && nums.length > 2) {
// 初始化并对数组排序
Arrays.sort(nums);
//定位起始点元素右侧的两端指针
int l = 0, r = 0;
for (int i = 0; i < nums.length; i++) {
// 如果起始点元素大于0,由于已排序,
// 其与右侧两端元素之和必然大于0
if (nums[i] > 0) break;
// 如果起始点右移,当前元素与之前相同
// 则需要跳过避免出现重复结果
if (i > 0 && nums[i] == nums[i - 1]) continue;
// 定义起始点元素右侧的两端指针
// 分别指向其右侧元素数组的左右两端
l = i + 1;
r = nums.length - 1;
while (l < r)
if (nums[i] + nums[l] + nums[r] == 0) {
// 当三数之和为0,则标记,并有序移动两端指针
// 与此同时跳过重复元素
while (l < r && nums[l] == nums[l + 1]) l++;
while (l < r && nums[r] == nums[r - 1]) r--;
l++;
r--;
}
// 如三数之和小于0,则左指针右移,增大三数之和
else if (nums[i] + nums[l] + nums[r] < 0) l++;
//如三数之和大于于0,则右指针左移,减小三数之和
else if (nums[i] + nums[l] + nums[r] > 0) r--;
}
}
}以上仅为参考,解题思路万千并非唯一,请结合具体案例编写测试用例验证正确性。同时也请进一步思考是否有更优的算法。
参考资料:
https://leetcode-cn.com/problems/3sum/solution/hua-jie-suan-fa-15-san-shu-zhi-he-by-guanpengchn/
原文:https://blog.51cto.com/15015181/2556401