二维费用的背包问题

题目链接acwing8


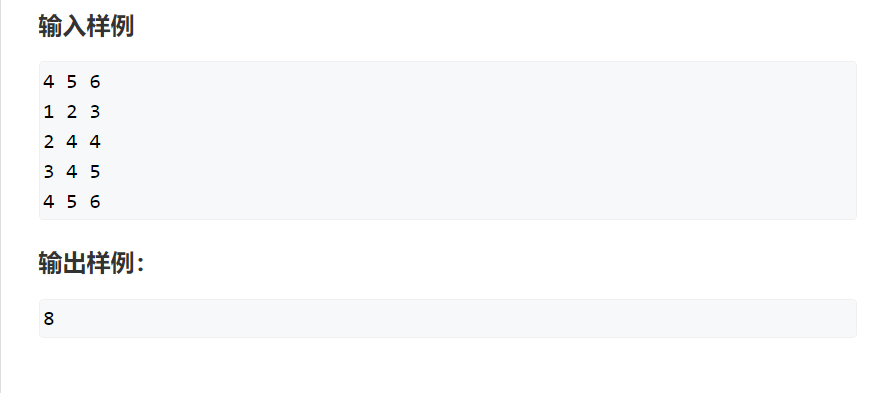
这道题目跟01背包问题很像，只不过是在01背包的基础加上了一个重量限制。
01背包问题的动态转移方程是

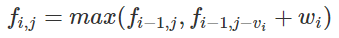
那么这个多了个重量，那么可以再开一维，变成三维

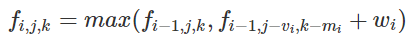
同01背包，它可以压缩亿下空间，于是变成了

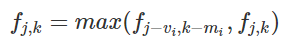
状态转移方程出来了，那么写代码也轻松了.

#include <bits/stdc++.h>

using namespace std;

int n, V, M;
const int N = 1e3 + 5;
int v[N], m[N], w[N], f[N][N];

signed main () {
    cin >> n >> V >> M;
    for (int i = 1; i <= n; i ++) {
        cin >> v[i] >> m[i] >> w[i];//体积，重量，价值
    }
    for (int i = 1; i <= n; i ++)
        for (int j = V; j >= v[i]; j --)
            for (int k = M; k >= m[i]; k --)
                f[j][k] = max (f[j - v[i]][k - m[i]] + w[i], f[j][k]);//动态转移方程，01 背包的思路
    cout << f[V][M];
} 

作者：sky_风
链接：https://www.acwing.com/solution/content/23631/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

二维费用的背包问题

原文：https://www.cnblogs.com/hnkjdx-ssf/p/14054888.html