本文主要推导两个高斯分布的相加结果。在知乎上有个问题:正态分布随机变量的和还是正态分布吗? _ 也是本文主要解决的问题。
高斯分布的概率密度函数: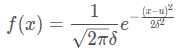
直觉中,两个高斯(正态)随机变量的和似乎应该是两个概率密度函数的和,如下图所示,其结果就近似为两个概率密度的包络线,这明显是错误的,是用直觉推导数学,大错特错。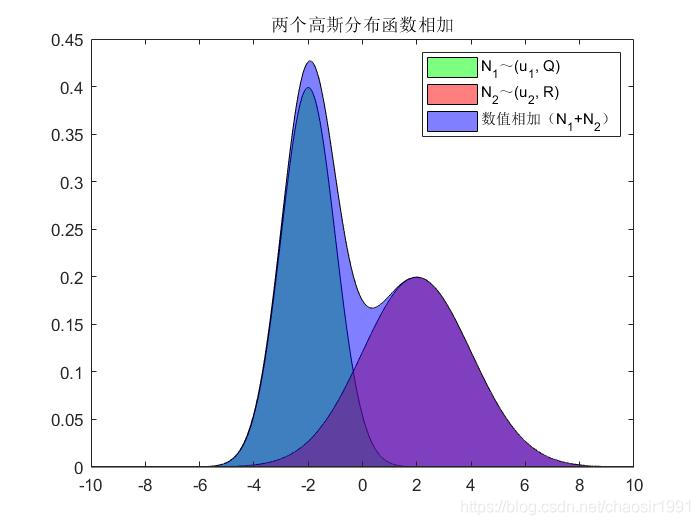
在解决此问题前,我们需要搞清楚两个高斯函数的和的物理意义,这里用经典的投骰子作为为例子更好理解。


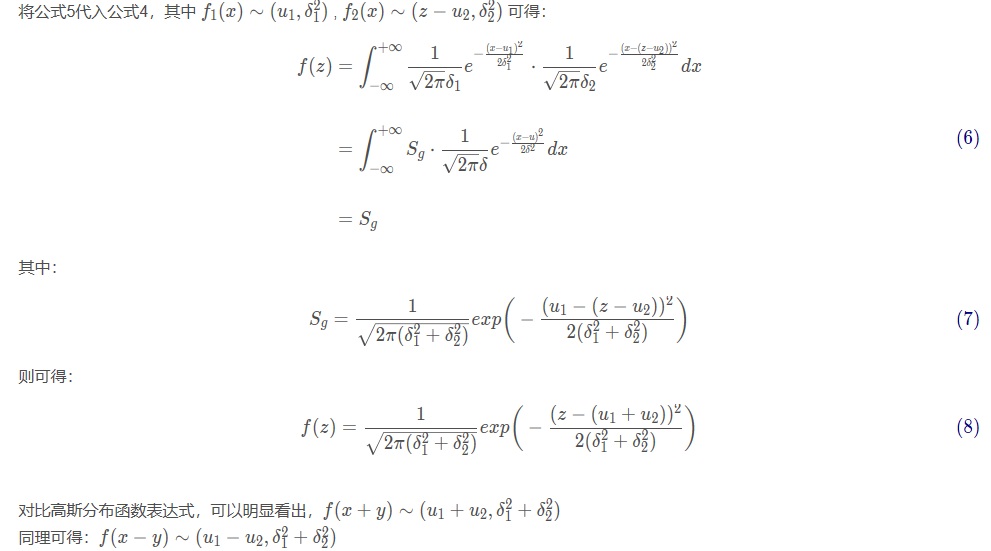


下面介绍两个高斯分布的和的分布——即正态分布的再生性的推导过程。


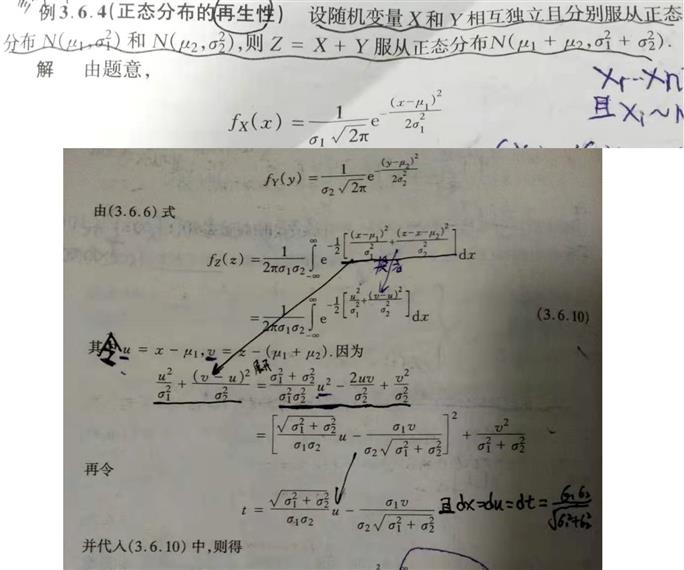
参考文献:两个高斯分布相加(卷积)的理论推导
原文:https://www.cnblogs.com/rainbow70626/p/14070413.html