题目链接:POJ3079 K-Anonymous Sequence
题目大意:
\(T\) 组数据,有一个长度为 \(N\) 的单调不下降的序列 \(A\) ,每一次操作可以将其中一个数字 \(A_i\) 减1,要求操作后的序列满足每个数字都存在至少 \(k-1\) 个元素和其大小相等,求操作数的最小值。
\(T\leq 20,2\leq N\leq 500000\) ,\(\forall A_i\in [0,500000]\)
思路:
设 \(dp[i]\) 为对于前 \(i\) 个数的最小值,\(sum[i]=\sum_{j=1}^i{a_i}\),显然将连续的一段 \(A_i\) 变为同一个值是较优的,首先可以得到 \(O(n^2)\) 的朴素DP:
考虑优化,将与 \(j\) 无关的项移到外面,简单整理:
这里有 \(i*a[j+1]\) 的乘积式,可以斜率优化,将min去掉,移项后可以得到:
将 \(dp[j]+j*a[j+1]-sum[j]\) 作为纵坐标, \(a[j+1]\) 作为横坐标,由于后者和斜率 \(i\) 都是单调递增的,可以用单调队列直接维护凸壳,时间复杂度 \(O(n)\)。
实现细节:
Code:
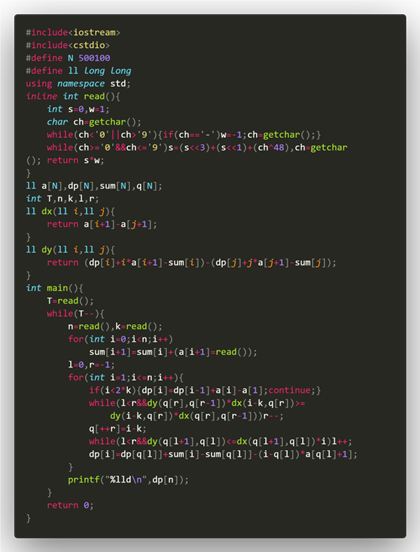
POJ3079 K-Anonymous Sequence (斜率优化)
原文:https://www.cnblogs.com/Neal-lee/p/14070846.html